基本介紹
- 中文名:拓撲環
- 外文名:Topology Torus
- 領域:拓撲學
環面
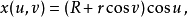
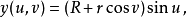

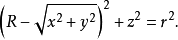
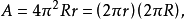
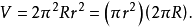
拓撲
- (x,y) ~ (x+1,y) ~ (x,y+1).
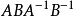
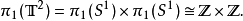
參看
- 代數環面
- 極大環面
- 周期格
- 環體
- 環面 (原子物理)
- Villarceau圓
- 環面曲線

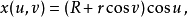
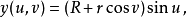

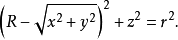
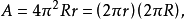
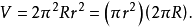
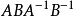
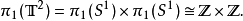
拓撲學上,拓撲環是一個定義為兩個圓的積的閉合曲面,若採用三維歐幾里得空間誘導的相對拓撲,則同胚於一個拓撲環面,只要它不和自己的軸相交(具體定義見正文)。...
環型拓撲是使用公共電纜組成一個封閉的環,各節點直接連到環上,信息沿著環按一定方向從一個節點傳送到另一個節點。環接口一般由傳送器、接收器、控制器、線控制器...
拓撲空間是一種數學結構,可以在上頭形式化地定義出如收斂、連通、連續等概念。拓撲空間在現代數學的各個分支都有套用,是一個居於中心地位的、統一性的概念。拓撲...
拓撲群又名連續群,是具有拓撲空間結構的群。在數學中,拓撲群是群 G 和與之一起的 G 上的拓撲,使得這個群的二元運算和這個群的取逆函式是連續的。拓撲群允許...
《法蘭西數學精品譯叢·拓撲學教程:拓撲空間和距離空間、數值函式、拓撲向量空間(第2版)》中的基本概念幾乎都在其一般形式下來介紹,並通過例子來說明所選擇定義的...
誘出模糊拓撲(induced fuzzy topology)是一類特殊的模糊拓撲。它是由給定分明拓撲誘導出的模糊拓撲。設(X,T)是普通的拓撲空間,以ω(T)記從(X,T)到[0,1]上...
《拓撲學教程拓撲空間和距離空間、數值函式、拓撲向量空間》是2009年高等教育出版社出版的圖書,作者是G.肖蓋。...
扎里斯基環是一種特殊的諾特拓撲環。設 (R,m) 是一個諾特局部環,則帶有 m 進拓撲的環 R 是典型的扎里斯基環的例子。...
3、接入層拓撲環當網路中存在環路,就會造成每一幀都在網路中重複廣播,引起廣播風暴。要消除這種網路循環連線帶來的網路廣播風暴可以使用STP協定(生成樹協定),以網路...
在數論中,阿代爾環(法文:adèle,英譯多用原文)又名賦值向量環,是由一個域 F 的所有完備化構成的拓撲環AF,原域F 可以對角方式嵌入其中。在現代代數數論中,賦值...
RPR(Resilient Packet Rings) 是由IEEE 802.17工作組正在開發的一個標準,以最佳化在MAN拓撲環上數據包的傳輸。該技術結合IP的智慧型化、乙太網的經濟性和光纖環網的...
