基本介紹
應力波是
應力和
應變擾動的傳播形式。在可
變形固體介質中機械擾動表現為
質點速度的變化和相應的應力、
應變狀態的變化。應力、應變狀態的變化以波的方式傳播,稱為應力波。通常將擾動區域與未擾動區域的界面稱為
波陣面,波陣面的傳播速度稱為
波速。
地震波、固體中的聲波和
超音波等都是常見的應力波。應力波的研究同地震、爆炸和
高速碰撞等
動載荷條件下的各種實際問題密切相關。在
運動參量不隨時間變化的
靜載荷條件下,可以忽略
介質微元體的
慣性力,但在運動參量隨時間發生顯著變化的動載荷條件下,介質中各個微元體處於隨時間變化著的動態過程中,特別是在爆炸或高速碰撞條件下,載荷可在極短歷時(
毫秒、微秒甚至納秒量級)內達到很高數值(10
10、10
11甚至10
12帕量級),
應變率高達10
2~10
7秒
-1量級,因此常需計及
介質微元體的
慣性力,由此導致對
應力波傳播的研究。對於一切具有慣性的可
變形介質,當在應力波傳過物體所需的時間內外載荷發生顯著變化的情況下,介質的運動過程就總是一個應力波傳播、反射和相互作用的過程,這個過程的特點主要取決於材料的特性。應力波研究主要集中在介質的非定常運動、
動載荷對介質產生的局部效應和早期效應以及載荷同介質的相互影響(見
衝擊載荷下材料的力學性能),研究時需要考慮材料在高
應變率下的動態力學性能和靜態力學性能的差別。問題的複雜性在於,應力波分析是以已知材料動態力學性能為前提的,而材料動態力學性能的實驗研究又往往依賴於應力波的分析。
 應力波相關圖書
應力波相關圖書研究簡史
描述和分類
應力波
波速的描述與參考
坐標系的選擇有關,若以
X表示在物質坐標中波陣面沿其傳播方向的位置,
t表示時間,則
C=d
X/d
t稱為物質波速或內稟波速。若以
x表示在空間坐標中波陣面沿其傳播方向的位置,則
c=d
x/d
t稱為空間波速。兩種波速是同一
物理現象的不同表述方式。對於
平面波,兩種波速的關係是:
c=v+(1+ε)C,
對於
本構關係不依賴於
應變率的所謂速率無關材料,如彈性體、
彈塑性體等,相應地有
彈性波、彈
塑性波等;對於本構關係依賴於應變率的所謂速率相關材料,如粘彈性體、粘彈塑性體等,相應地有粘彈性波、粘彈塑性波等。
應力波按
波陣面幾何形狀分為平面波、
柱面波、
球面波等;按質點速度擾動與波傳播方向的關係分為縱波和橫波;按
介質受力狀態分為拉伸波、
壓縮波、扭轉波、
彎曲波、拉扭
複合波等;按控制方程組是否為
線性分為線性波和
非線性波。按介質連續性要求,質點位移
u在波陣面上必定連續,但其
導數則可能間斷,數學上稱為奇異面。若
u的
一階導數間斷,即
質點速度和
應變在波陣面上有
突躍變化,則稱為一階奇異面或強間斷,這類
應力波稱為
激波或
衝擊波(見
固體中的激波)。若
u及其一階導數都連續,但其二階導數(如
加速度)間斷,則稱為二階奇異面,這類應力波稱為加速度波。依次類推,還可以有更高階的奇異面,統稱弱間斷,都是連續波。奇異面理論在應力波研究中具有重要意義。
平面波情況最簡單,表現最典型,研究得也最充分。以下以平面波為例,說明不同材料中應力波的傳播特性及其與
介質的相互作用。
速率無關材料中的應力波
式中
。方程(1)有兩族分別代表右
行波和左行波的實特徵線和相應的沿特徵線的
相容關係:
式中波速
C和波阻抗
ρ0C完全由材料性能決定。此結果與氣體動力學中的一維非定常運動相類似。求解
應力波的傳播問題在數學上歸結為在給定的初始和
邊界條件下求解
波動方程⑴或等價的特徵線方程組⑵。常用的數值解法有
特徵線法、有限差分方法和
有限元法。
對
各向同性線彈性材料,d
σ/d
ε為常數,因此線彈性波波速(即
聲速)
Ce為恆值:對於
一維應力縱波為
C0=(
E/
ρ0)
1/2,式中E為
楊氏模量;對於側向受限的一維
應變縱波為C
1=(E′/ρ
0)
1/2,側限
彈性模量
對
彈塑性材料,隨
應力波幅值的增大,一旦滿足
屈服條件將傳播塑性波。例如,在一維應力作用下,當
σ超過單軸屈服限
Y0時傳播塑性波,波速直接由單軸應力-
應變曲線塑性段的
斜率按式⑴確定。對一維應變縱波,按米澤斯或特雷斯卡屈服條件,當軸向應力超過側限屈服限(許貢紐彈性限)
σHKL=
Y0(1-
ν)/(1-2
ν)時,傳播塑性波,波速
=
[(
K+4
Gp/3)/
ρ0]1/2,式中塑性強化
模量G
p=μY'Y/(3μ+Y'Y),其中Y為考慮強化的作為塑性功W
p函式的
屈服應力,Y'=(dY/dW
p)≥0。對理想塑性體Gp=0,
等於體積
彈性波速(K/ρ
0)
1/2。由於材料
應力-
應變曲線的塑性段
斜率通常小於彈性段斜率,則由式⑴知塑性波速通常小於
彈性波速,即
塑性波總尾隨在彈性前驅波的後面。由式⑴還可知:對於遞增強化材料,應力-應變曲線下凹(即
),高波幅處擾動傳播速度大於低波幅處擾動傳播速度,從而形成
激波(圖1a上部為應力-應變曲線,中、下部表示波速和波結構);對於遞減強化材料,應力-應變曲線上凸(即
),高波幅處擾動傳播速度小於低波幅處擾動傳播速度,在波的傳播過程中波形將變得愈來愈平坦(圖1b);對於線性強化材料,(即
),
塑性波波速為恆值
(E1/
ρ0)1/2,
E1為線性強化
模量(圖1c)。有關塑性載入波的結論也適用於非線性
彈性波。另見塑性波。
 應力波相關圖書
應力波相關圖書圖1 在恆定外載作用下具有不同強化特性的
彈塑性桿中一維應力波傳播示意圖
卸載波
彈性變形的可逆性意味著載入和卸載遵循相同的
應力-
應變關係,所以
彈性波傳播中的卸載問題不需另行處理;塑性變形的不可逆性則意味著載入和卸載遵循不同的應力-應變關係。實驗表明彈塑性材料從塑性變形狀態卸載時一般遵循
胡克定律。按此,卸載擾動以彈性波速
Ce傳播。這樣,彈塑性材料的動態加、卸載過程是一個以較快波速
Ce傳播的卸載擾動與以較慢的
塑性波波速
Cp傳播的塑性載入擾動相互作用的過程,
介質中彈性卸載區和塑性載入區的界面不斷變化著。因此,對
彈塑性材料動態加卸載問題的求解可歸結為在給定的
初始條件和
邊界條件下聯立求解塑性載入區和彈性卸載區的兩組不同的
波動方程。問題的複雜性在於,求解
聯立方程要求在兩區邊界上滿足
運動學和
動力學相容條件,而此邊界卻是在解題中才能確定的。此外,卸載後的介質還可發生第二次塑性載入及隨後的卸載,所以一般難以得到方程組的解析解,故多採用數值解法。在
彈性波速
Ce比
塑性波速
Cp大得多的情況下,可作剛性卸載假定(相當於
Ce→∞),使問題簡化為剛
塑性動力學問題。
速率相關材料中的應力波
對於速率相關材料,其力學回響通常可概括為兩部分:與速率無關的
瞬態回響和與速率相關的非瞬態回響,而各種非瞬態回響可歸結為由具有粘性性質的內耗散力所引起。這樣,對於在彈性回響的基礎上計及速率相關性的
粘彈性介質,如高分子材料等,相應地有
粘彈性波。粘性效應的主要體現是波傳播中的
彌散現象(波速依賴於頻率)和
吸收現象(波幅隨傳播距離而衰減)。類似地,對於在
彈塑性回響的基礎上計及速率相關的介質,相應地有粘彈
塑性波。如果只對塑性部分計及粘性效應則相應地有彈粘塑性波,其總
應變率 由瞬態的彈性應變率
0和非瞬態的
粘塑性應變率 組成,而
取決於所謂超
應力,即實際應力
σ與準靜態應力-應變關係所決定的
平衡態應力
σe(
ε)之差。在一維情況下有:
式中函式
g稱為鬆弛函式。這類彈粘
塑性波的主要特點是:波的傳播速度由材料
瞬態回響決定,故彈
粘塑性波速等於
彈性波速,而大於速率無關材料中的塑性波速;由於內耗散力的粘性效應,波在傳播中將不斷衰減。
應力波的反射透射
應力波到達物體邊界或不同波阻抗材料的界面時,將發生反射和透射,常引起材料的斷裂破壞。
以
彈性波為例:對於法向入射波,當在固定邊界反射時,
反射波與入射波應力等值同號,即應力的總和恰好是入射波應力值的兩倍;當在自由邊界反射時,反射波與入射波應力等值異號,而
質點速度的總和恰好是入射波質點速度值的兩倍。對於斜入射的彈性縱波或橫波,一般將同時反射和透射縱波和橫波。在
介質自由表面處,與波的
繞射現象相關,還可能產生一種沿著介質表面傳播的彈性
表面波(例如
瑞利波),它是縱波與橫波
耦合形成的一種非
均勻平面波,波幅隨著距自由表面的深度呈指數衰減,波速
Cs略低於橫波波速
Ct(見前表,表中
k為一常數,對不同材料數值不同),且與頻率無關(即無頻率
彌散現象)。彈
塑性波的反射有時會出現反射卸載,形成非常複雜的波系。
反射斷裂是由
應力波反射所造成的斷裂現象。在材料和工程結構的動態斷裂研究中具有重要意義。當由壓縮載入波和隨後的卸載波所組成的壓力脈衝入射到
介質自由表面時,
壓縮波部分首先卸載反射為拉伸波,它與入射壓力脈衝中的卸載波部分相互作用後,將在鄰近自由表面處造成拉應力,一旦滿足動態斷裂準則即導致斷裂,這種斷裂稱為層裂(圖2a)。裂片從背面飛出。同時,由於形成了新的自由表面,又會使繼續入射的壓力脈衝在新表面反射而造成第二層層裂。依次類推有可能造成多層層裂。類似地,由兩自由表面反射的拉
應力波在物體心部或角部等處相遇而相互作用後,可導致心裂和角裂等(圖2b和圖2c)。一般來講,材料本身或材料間的聯結往往可承受強壓縮而經不起拉伸,因而反射斷裂是動態破壞的一種重要形式。軍事上的
碎甲彈和
爆炸力學實驗技術中的飛片技術都是據此原理髮展而成的。
 圖2 反射斷裂示意圖
圖2 反射斷裂示意圖圖2 反射斷裂示意圖
發展趨勢
應力波研究當前發展的主要動向為:進一步由一維理論向二維和三維理論發展,向複合載荷條件下的應力波研究發展;由小變形向大變形的應力波研究發展;由
應變率無關理論向應變率相關理論發展;由純力學應力波向熱-力學
耦合的應力波研究發展;由
各向同性介質向
各向異性和複合材料中的應力波研究發展;以及向更廣泛地採用電子計算機和尋找新的測量短歷時、高強度的動態過程的實驗技術發展。
參考書目
H.考爾斯基著,王仁等譯:《固體中的應力波》,
科學出版社,北京,1958。(H. Kolsky,
Stress Waves in Solids,Oxford Univ, Press,London,1953.)
J. S. Rinehart,Stress Transients in Solids,John S. Rinehart,Santa Fe,New Mexico,1975.
W. K. Nowacki,Stress Waves in Non-elastic Solids,Pergamon Press,London,1978.
 應力波相關圖書
應力波相關圖書


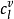



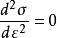
 應力波相關圖書
應力波相關圖書




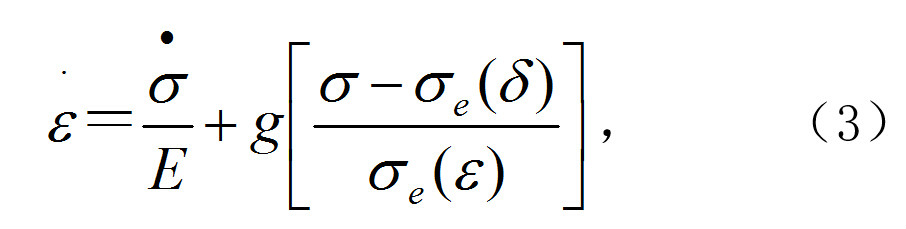
 圖2 反射斷裂示意圖
圖2 反射斷裂示意圖 應力波相關圖書
應力波相關圖書


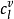



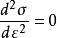
 應力波相關圖書
應力波相關圖書




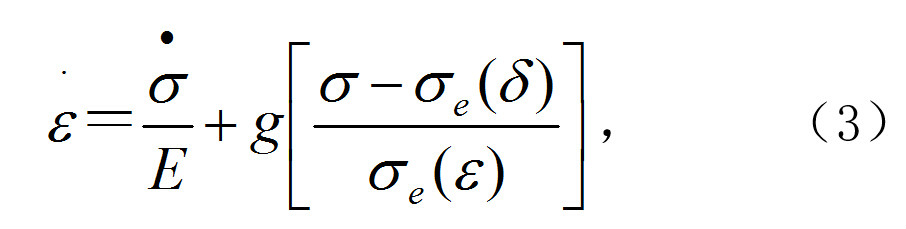
 圖2 反射斷裂示意圖
圖2 反射斷裂示意圖