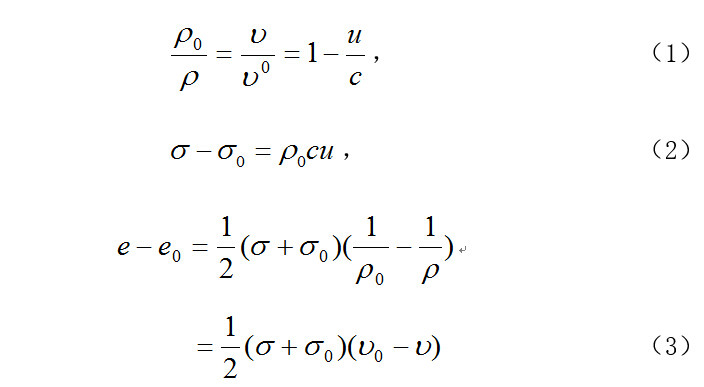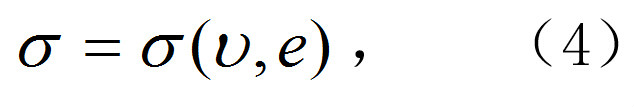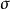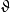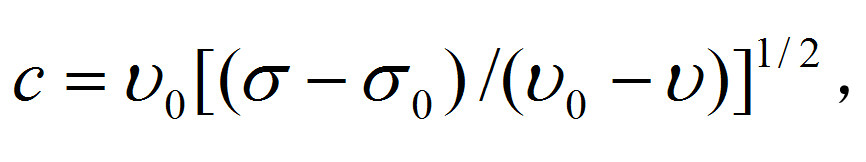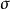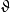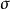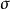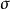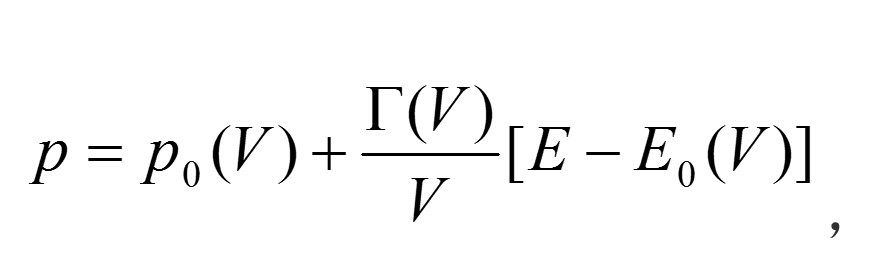固體中的激波

固體中應力、應變和質點速度在波陣面上發生突躍變化的一種應力波。幾乎所有固體在壓縮到某一程度後都會愈來愈難壓縮，當一個連續變化的壓縮應力波在固體中傳播時，固體的這種非線性壓縮特性使得高波幅處的波速大於低波幅處的波速，後載入的高波幅處的擾動將追上先載入的低波幅處的擾動，波形前緣變得愈來愈陡，最終發生應力、應變和質點速度的突躍。這種突躍變化在熱力學上可看作是絕熱的但有熵增的不可逆過程，而在數學上可作為強間斷面來處理。另外還有一類在低壓時由邊界上強間斷形成的固體中的激波，如彈性激波和線性強化材料中的彈塑性激波，它們都以傳播速度恆定為特點。這一類突躍變化不引起額外的熵增。

基本介紹

• 中文名：固體中的激波
• 外文名：shock waves in solids

簡介

固體中的激波廣泛存在於各種強爆炸和高速碰撞過程中，例如地下核爆炸（見地下爆炸）、地震、隕石碰撞、高能炸藥與固體材料的接觸爆炸、彈頭對目標的高速撞擊等都會產生這種激波。在力學、固體物理學和地球物理學等研究領域中，可以利用固體中的激波在極短的時間內產生數百萬至上千萬巴的高壓（地心壓力的數倍，1巴等於帕）、數萬開的高溫和～秒的高應變率，以研究固體材料在這些極端條件下的物理特性和化學特性。

衝擊突躍條件和許貢紐線

如果一平面縱激波，它的前方和後方的介質（材料的初態和終態）都處於熱力學平衡態，根據跨過波陣面的質量、動量和能量守恆條件，在相對於激波前方材料為靜止的空間坐標系中，可得到聯繫初態和終態的密度ρ（或比容=1/ρ）、質點速度u、正應力σ（垂直於波陣面的應力，以壓應力為正）、比內能e和激波相對前方介質的空間波速c之間的關係，可用下式表示（下標0表示初態值）：

這些關係式是激波的基本方程，它們所表達的關係稱為衝擊突躍條件。對於曲面波陣面，在法線方向這些關係式也同樣成立。

如果已知給定材料的狀態方程，例如固體激波研究中用的內能形式的狀態方程：

則對於一定的初態，方程（1）～（4）中包含終態的、e和波速c共五個未知參量。指定其中任意一個，就可確定其餘四個，即可建立任意兩參量間的關係。如果材料的狀態方程未知，則需由實驗測定其中任意兩參量間的關係，再由式（1）～（3）確定與其他參量間的關係。這樣的聯繫任意兩終態參量間的關係式稱為蘭金-許貢紐方程，簡稱許貢紐線，又稱衝擊絕熱線。許貢紐線有多種形式，常用的有下列三種（圖1）：

①-根據式（1）和（2）可以得到如下關係：

即波速c由-許貢紐線上聯接初態和終態的弦線的斜率所確定，此弦線稱為瑞利線（圖1a）。由式（3）可知，瑞利線下的梯形面積代表比內能的衝擊突躍。對於正常材料，許貢紐線是下凹的，顯然c隨σ增大而增大。

②-u線由式（2）可知，-u許貢紐線上終態和初態聯線的斜率代表材料的衝擊阻抗p1c（圖1b）。在討論激波相互作用、反射和透射等問題時，界面上應滿足σ和u均連續的條件，用-u許貢紐線來處理最方便。

③c-u線在激波實驗中，c和u較易測定。因此c-u許貢紐線是材料高壓狀態方程實驗研究中最常用的。特別是，對廣泛材料所作的大量試驗表明，在一相當寬的試驗壓力範圍內，如果不存在衝擊相變，則c和u之間有簡單的經驗關係（圖1c）：

式中a0和s為材料常數（a0常接近於材料的體積聲速），某些實測值見下表。對於個別材料（如低碳鋼），上式中需添加一個u的二次項。

某些材料的、s、、實測值

材料	硬鋁; （Al/Cu/Mg/; Mn:93.4/; 4.5/1.5/0.6)	銅	低碳鋼*; (C:0.18%)	鈾鉬合金; (U/Mo: 97/3)	碳化鎢	聚乙烯; (低密度)	有機; 玻璃; (Lucite)	環氧樹脂(含乙二胺14%)	酚醛樹脂(Durite)
a0(毫米/微秒)	5.328	3.940	3.574	2.565	4.920	2.900	2.260	2.678	2.874
s	1.338	1.498	1.920	1.531	1.339	1.481	1.816	1.530	1.404
p0(克/厘米)	2.785	8.930	7.850	18.450	15.020	0.915	1.181	1.198	1.370
	2.000	1.990	1.690	2.030	1.500	1.644	0.750	1.130	0.500

許貢紐線上的溫度和熵可由式（3）和熱力學第一、第二定律算得；隨激波壓力的提高，溫度可達足以引起熔融的程度。若材料比熱小，可壓縮性大，孔隙率高，則衝擊溫度高。

常用模型

根據材料的力學性能和材料所受載荷的大小，常用的激波模型有：

①流體動力學模型應力張量可寫成球量和偏量之和，在平面激波的一維應變條件下，式（1）～（4）中的σ可寫成流體靜水壓p和最大剪應力相關項之和，即

p隨體積壓縮量的增加而增大，在目前技術下可高達～帕量級；則隨剪應變的增大而增大，但以材料剪下強度為限，對於大多數工程材料不超過帕量級。當激波應力比材料剪下強度大得多時，項可忽略不計，式（1）～（4）中的σ均可代之以p。這相當於把固體當作無粘性可壓縮流體處理，這種處理方法稱為“流體動力學近似”方法。用此方法，氣體動力學中激波研究的許多結果都可套用於固體中激波的研究。

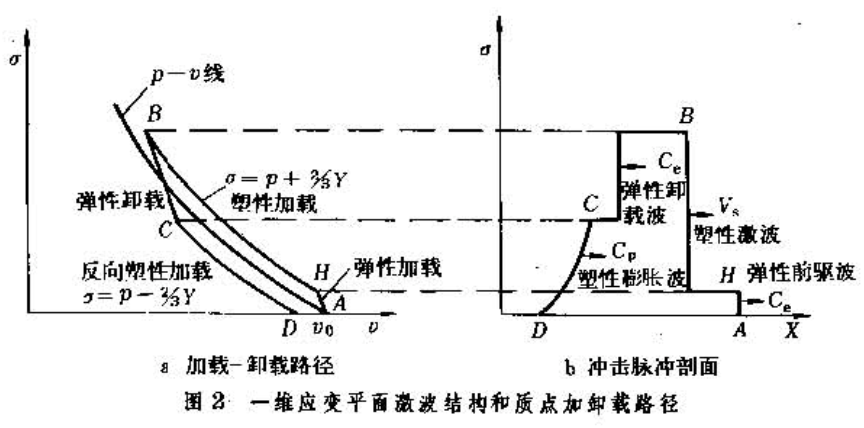
②流體彈塑性體模型在流體動力學模型基礎上再按彈塑性理論考慮剪下強度效應的模型。當σ接近於屈服應力時，就需計及材料的剪下強度效應。假設塑性變形對體積壓縮不起作用，式(6)的流體靜水壓部分仍和流體動力學近似中一樣考慮，而最大剪應力部分按彈塑性理論中的畸變律考慮（例如按米澤斯或特雷斯卡屈服條件），這樣則有σ=p(v，E)±2Y/3，式中Y為考慮強化的屈服應力，它是塑性功的函式。對於強化材料，-dY/d>0；對於理想塑性材料，dY/dv=0，Y=Y0（單軸應力屈服限），屆服後的σ-V線與流體動力學近似中的p-V線平行(圖2a)。由此可知，載入時形成雙波結構，較慢的塑性激波尾隨在較快的彈性前驅波之後，而卸載時初始階段是彈性卸載，當卸載應力又滿足屈服條件（反向屈服）時，則尾隨一塑性膨脹波。圖2a表示某時刻激波掃過應變率無關的流體彈塑性材料時材料質點的載入和卸載情況，圖2b為衝擊脈衝結構，反映出應力沿物質坐標X上的分布，圖中的虛線使材料中某點處的波的作用與該點的載入和卸載情況對應起來。有關流體彈塑性體的特性見流體彈塑性體。

特點

研究固體中的激波除了考慮固體剪下強度效應外，還要在狀態方程中考慮到點陣結合力以及相變對激波的影響，分述如下：

①固體高壓狀態方程固體中分子（或原子、離子等）是以有序排列方式作周期性重複排列而構成點陣的，彼此間相互作用強烈，因此，即使在流體動力學近似下，其狀態方程也比氣體的複雜。內能E除包括由點陣熱振動和電子熱激活能等組成的熱能Et（動能）外，還包括由分子（或原子、離子等）間的相互作用能（點陣結合能）和零點振動能以及價電子氣壓縮能等組成的冷能（勢能）E0。相應地壓力p由熱壓Pt和冷壓P0(P0=-dE0/dv)兩部分組成。目前最常用的是以固體物理學或物理力學中有關點陣準諧振動理論為基礎的格呂內森狀態方程：

式中V為體積，E為內能；假定它只是V的函式。工程近似計算中有時取格呂內森係數/V為常數。某些材料在室溫零壓下的格呂內森係數和值見上頁表。

②相變固體在一定的衝擊高壓高溫作用下會發生相變，在許貢紐線上相應地出現間斷（一級相變）或斜率的間斷(二緩相變)。當激波壓力超過相變壓力不多時，高壓相中激波波速c2會低於低壓相中激波波速c1，從而形成雙波結構，直到激波壓力高到使時c2>c1（臨界值稱為過驅壓力），才又形成穩定的單一激波。激波與相變的相互關係已被用來作為研究相變的手段，例如通過激波發現鐵在130千巴衝擊壓力下發生α相（體心立方）向ε相（密排六方）的相變，還利用激波與相變的關係作為達到某種所需相變的手段（例如爆炸合成金剛石工藝中石墨向金剛石的相變），並在探索用激波技術實現氫向金屬相的轉變（見衝擊載荷下材料的力學性能）。