對稱張量是各分量關於指標對稱的張量,表示r階反變張量全體。x是對稱張量的充分必要條件是它的分量關於各指標是對稱的,x是反對稱張量的充分必要條件是它的分量關於各指標是反對稱的。
基本介紹
- 中文名:對稱張量
- 外文名:symmetric tensor
- 所屬學科:數學
- 適用範圍:數理科學
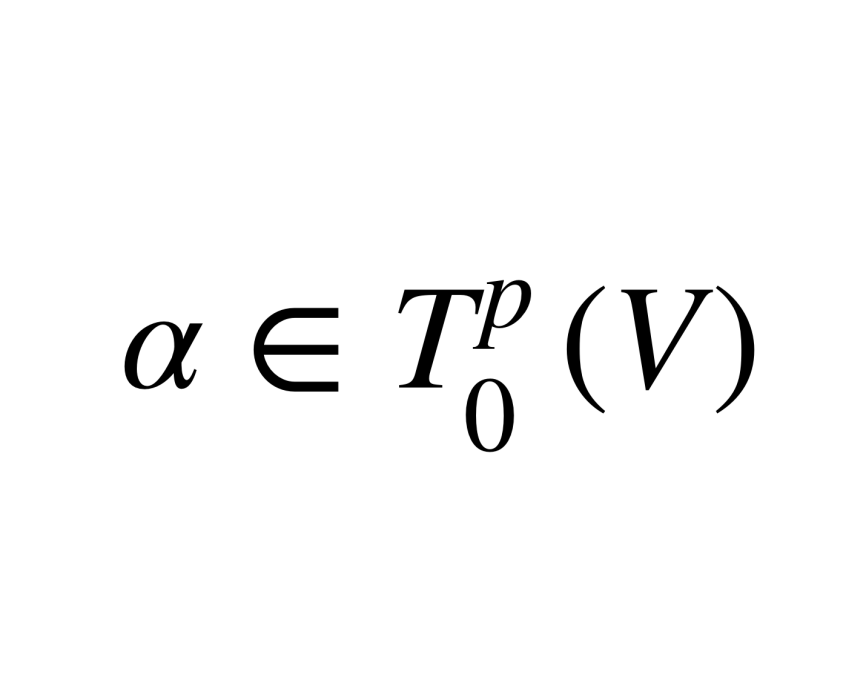
對稱張量是各分量關於指標對稱的張量,表示r階反變張量全體。x是對稱張量的充分必要條件是它的分量關於各指標是對稱的,x是反對稱張量的充分必要條件是它的分量關於各指標是反對稱的。
對稱張量是各分量關於指標對稱的張量,表示r階反變張量全體。x是對稱張量的充分必要條件是它的分量關於各指標是對稱的,x是反對稱張量的充分必要條件是它的分量關於...
張量(tensor)理論是數學的一個分支學科,在力學中有重要套用。張量這一術語起源於力學,它最初是用來表示彈性介質中各點應力狀態的,後來張量理論發展成為力學和物理學...
完全對稱化子(completely symmetrizer)是張量空間上的一種投影運算元,有時也稱為對稱化子。多重線性代數的重要概念。定義有張映射的一種向量空間。具體定義有多種不...
對稱面有多個義項。一個是指群論在化學中的套用,一個是指結晶學名詞,還有一個是幾何學的對稱面。...
能動張量Tab是一個對稱的二階張量,是描述物質運動狀況的物理量。全稱能量動量張量,又名應力能量張量。...
曲率張量(curvature tensor)由聯絡確定的一個重要張量。曲率張量是一個重要的數學量。在眾人所關注的廣義相對論中起到了重要的作用。沒有曲率張量,就不可能建立起...
對稱化運算元(symmetrization operator)是作用於反對稱張量上的運算元。張量是向量概念的綜合,可用以代表各向量間的關係。例如彈性張量把彈性體上每一點的變形與外加應力...
與外代數,對稱代數,張量代數,克利福德代數等一起,代數結構在多重線性代數中也建立了起來.對稱代數對稱代數 編輯 對稱代數是概括多元多項式代數的一種代數。設E是...
電磁張量(electromagnetic tensor)或電磁場張量(electromagnetic field tensor)(有時也稱作場強張量(field strength tensor)、法拉第張量(Faraday tensor)或麥克斯韋雙矢量...
從巨觀角度描述各向異性晶體的物理性能,並研究晶體的對稱性和晶體點陣對稱性之間的關係,簡化有關的物理方程,是一種唯象的處理方法。早在19世紀就已經系統地和完整地...
應力一能量張量(stress-energy tensor)由映射確定的一個特殊張量.若f:M->N是光滑映射,M和N的黎曼度量張量分別為g和h,f的能量密度為。(f),則"Sf=e }.f ...
研究大變形時用瞬態構形來描述的對稱應力張量。... 這裡,便是柯西應力張量,它是二階對稱張量。圖集 柯西應力張量的概述圖 V百科往期回顧 詞條統計 瀏覽次數:...
應力張量,是指是應力狀態的數學表示。... 數學上應力為二階張量,三維空間中需九個分量(三個正應力分量和六個剪應力分量)來確定。在靜力平衡(無力矩)狀態下,剪...
張量空間(tensor space)是多重線性代數的重要概念,定義是有張映射的一種向量空間。多重線性代數式代數學的一個重要分支。可以將它看做是線性代數的發展。它是伴隨...
《張量分析及在力學中的套用(第2版)》系統闡述了張量分析及其在力學中的套用。全書共分9章,第1,2章介紹張量的基礎知識,第3~6章介紹張量代數、張量分析和黎曼...
。特別地(見下),測地線方程確定聯絡的對稱部分,而撓率張量確定反對稱部分。扭率張量撓率形式 撓率形式,是撓率的另一種刻畫,適用於M的標架叢FM。這個主叢裝備有一...
《張量分析(第3版)》是2020年1月清華大學出版社出版的圖書,作者是黃克智、薛明德、陸明萬。...
反對稱化運算元(anti-symmetrization operator)是作用於反對稱張量上的運算元。... 反對稱化運算元(anti-symmetrization operator)是作用於反對稱張量上的運算元。
定義 伴隨張量(adjoint tensor)伴隨變換的推廣.設E",E是特徵為零的域K上的對偶空間,且dim=n.對任意z,EE"⑧E,由Ad(z zZ,...,z -O=DE(z},zZ,...,...
應變張量是應變狀態的數學表示。數學上應變為二階張量,二維平面中需四個分量,三維空間中則需九個分量(三個線應變分量和六個剪應變分量)予以確定。...
《張量分析及在力學中的套用(第2版)》是2014年出版的書籍,作者是余天慶、李厚民、毛為民。...
《彈性力學與張量分析》是2003年高等教育出版社圖書發行部(蘭色暢想)出版的圖書,作者是郭日修。本書供高等學校船舶與海洋工程等工程專業作研究生教材用,也可供高等...
在微分幾何中,黎曼曲率張量或黎曼曲率是表達黎曼流形的曲率的標準方式,更普遍的,它可以表示有仿射聯絡的流形的曲率 ,包括無撓率或有撓率的。...
《張量分析(第2版)(北京高等教育精品教材)》是2014年8月27日出版的圖書,作者黃克智等。...
與外代數,對稱代數,張量代數,克利福德代數等一起,代數結構在多重線性代數中也建立了起來。 [3] 混合張量代數結合代數 編輯 結合代數是類似於環、域,而更接近於...
《張量和連續介質力學》是2012年12月冶金工業出版社出版的圖書,作者是黃寶宗。... 1.8二階張量的轉置、行列式、加法分解和反對稱張量 1.8.1二階張量的轉置和行列...
