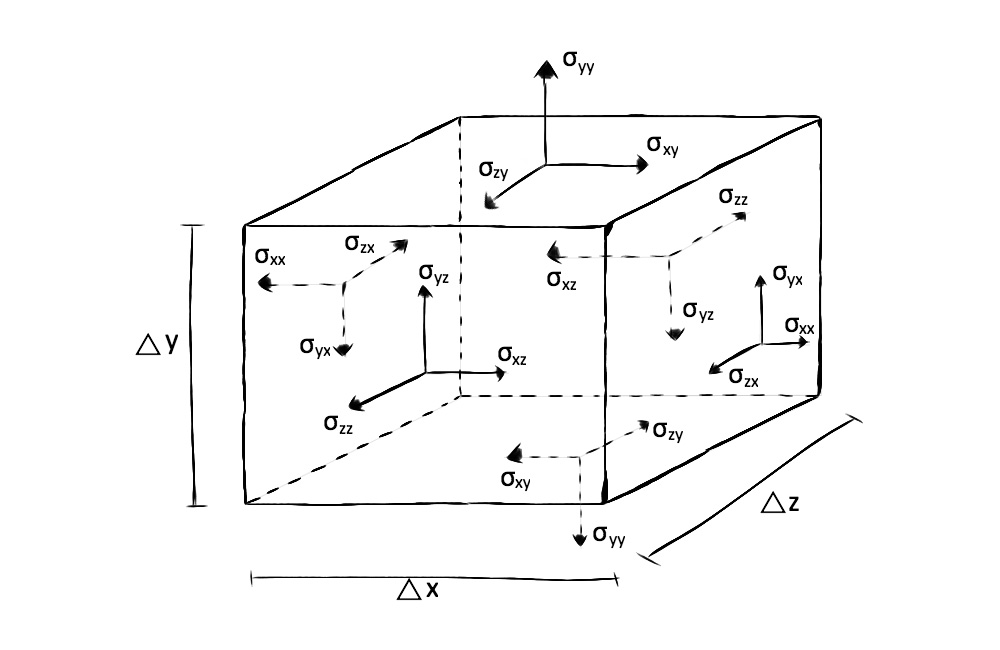
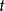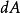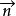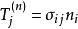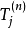研究大變形時用瞬態構形來描述的對稱應力張量。
基本介紹
- 中文名:柯西應力張量
- 外文名:Cauchy’s stress tensor
- 屬性:對稱應力張量
- 情況:在大變形(有限變形)情況下
柯西應力張量(Cauchy’s stress tensor)
在大變形(有限變形)情況下,由於變形前的初始構形和變形後的瞬態構形(見彈一塑性有限元法)差別較大,這樣分別定義在這兩個構形上的應力張量就很必要。所謂物體的一個構形是指由連續介質構成的某一物體某瞬間在空間所占的區域。
在大變形分析中柯西(Cauchy)應力張量是一種採用歐拉描述法(是以質點的瞬時坐標 和時間
和時間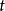 作為自變數描述)定義在
作為自變數描述)定義在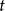 時刻的現時構形上的應力張量
時刻的現時構形上的應力張量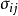 ,又稱歐拉應力張量。
,又稱歐拉應力張量。

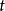
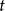
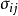
取三維空間笛卡兒坐標系,在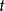 時刻的現時構形中截取一個四面體素,其斜面面元為
時刻的現時構形中截取一個四面體素,其斜面面元為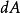 ,法線為
,法線為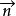 ,另外三個面元
,另外三個面元 取為與所取坐標面平行。由四面體素的平衡條件得出面上的應力為:
取為與所取坐標面平行。由四面體素的平衡條件得出面上的應力為: