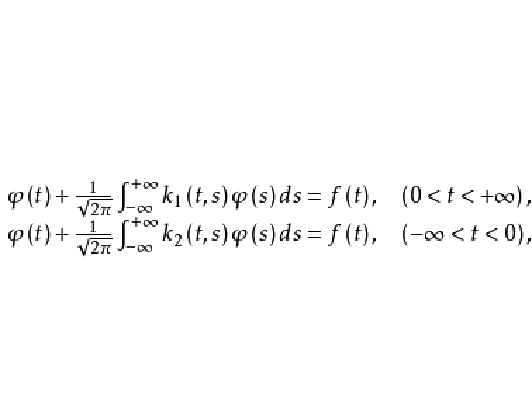基本介紹
其中
是未知函式。對偶積分方程常在
偏微分方程的混合邊界值問題中出現,特別地,當
是卷積核,即
時,它可化為
黎曼邊值問題去解決。為此,在方程中引入新未知函式
以及
其中
分別是
的傅立葉變換,上式消去未知函式
,即得到確定未知函式
的
黎曼問題:
它的離散形式是如下的對偶方程組
其中J是
貝塞爾函式,
。它的解是
蒂奇馬什(Titchmarsh,E,Ch.)用梅林變換得到的,它是
奇異積分方程
1.特徵值集有有限的極限點或有連續的譜。
2.對應一個特徵值可能有無窮多個特徵函式。
3.
齊次方程和轉置齊次方程的線性無關解的個數可能不相等。例如,拉列斯庫-皮卡(Lalescu-Picard)齊次方程
當
時,方程有非零解
,所以所有大於1/2的實數λ都是特徵值,即有連續譜。又如,傅立葉正弦變換產生的積分方程
奇異積分方程與
弗雷德霍姆積分方程的本質差異在於前者出現在方程中的積分運算元是有界運算元甚至是有逆的,而後者只是相應函式空間中的緊運算元,緊運算元除有限維運算元外是沒有有界逆的,這就是
弗雷德霍姆理論不能套用到奇異積分方程的根本原因。奇異積分方程的基本定理是諾特定理,
弗雷德霍姆定理是它當指標為零的特例。也正因為奇異積分方程的積分運算元不是緊運算元,所以奇異積分方程一般不會出現如同第一類弗雷德霍姆方程與第二類那種本質差別。
最重要的三類奇異積分方程是:
1. 柯西核的奇異積分方程(包括希爾伯特核的奇異積分方程),這是研究得最早和最完整的一類方程(其特點是未知函式出現在發散的積分號下,該積分只在柯西主值下有意義),以及和它的特徵方程有密切聯繫的黎曼問題。
3. 對偶積分方程。
人們在相當深入地研究了以上幾類奇異積分方程,以及它們相應的離散形式、方程組、高維的情形和各種各樣的推廣以後就企圖用統一的觀點去處理它們。統一的一個途徑是把它們作為一般的
維納-霍普夫方程。
奇異積分方程的蓬勃發展和它的套用的廣泛性是分不開的,它已被廣泛套用於彈性理論、薄殼理論、斷裂力學、電磁波衍射、大氣層輻射傳輸、中子遷移、控制論、隨機過程的預測和人口理論等領域.套用範圍還在不斷擴大。