弗雷德霍姆定理(Fredholm theorems)積分方程的基本定理.設第二類弗雷德霍姆積分方程是稱為方程(1)的轉置方程。
弗雷德霍姆定理(Fredholm theorems)積分方程的基本定理.設第二類弗雷德霍姆積分方程是稱為方程(1)的轉置方程.弗雷德霍姆定理或者說弗雷德霍姆理論是指以下四個定理:
1.(二者擇一定理)或者是非齊次方程(1)對任意給定的f(x)有惟一解,或者是方程(1)的齊次方程有非零解,二者必居其一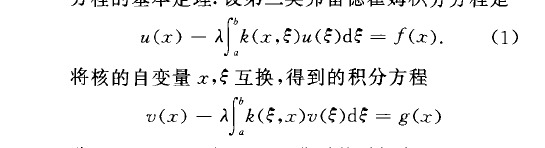
1.(二者擇一定理)或者是非齊次方程(1)對任意給定的f(x)有惟一解,或者是方程(1)的齊次方程有非零解,二者必居其一
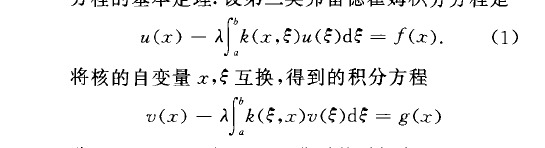
2.方程(1)的齊次方程和它的轉置齊次方程有有限個相同個數的線性無關解.
3 .當幾。是特徵值時,非齊次方程(1)有解的充分必要條件是已知函式f (x)滿足條件f}f(x)v;(x)dx一0(,一‘}2,一’,其中v; ( x)是轉置齊次方程的線性無關解,亦即f(x)與轉置齊次方程關於幾。的一切特徵函式正交.此時方程(1)的解取形式u(x)一uo}x)+藝c;}p(x)其中uo (x)是方程(1)的任一特解,尹是方程(1)的
齊次方程對應幾。的m個線性無關的特徵函式,。,是任意常數.
3 .當幾。是特徵值時,非齊次方程(1)有解的充分必要條件是已知函式f (x)滿足條件f}f(x)v;(x)dx一0(,一‘}2,一’,其中v; ( x)是轉置齊次方程的線性無關解,亦即f(x)與轉置齊次方程關於幾。的一切特徵函式正交.此時方程(1)的解取形式u(x)一uo}x)+藝c;}p(x)其中uo (x)是方程(1)的任一特解,尹是方程(1)的
齊次方程對應幾。的m個線性無關的特徵函式,。,是任意常數.
