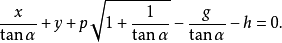圓錐曲線最早是由古希臘學者梅內克謬斯(Menaechmus)進行系統研究的，他用頂角分別為直角、銳角和鈍角，三種直圓錐以不過頂點而垂直一條母線的平面截割這三種圓錐曲面，而分別得到拋物線、橢圓和雙曲線的一支。
基本介紹
- 書名：圓錐曲線論
- 作者：阿波羅尼奧斯
- 類別：數學著作
- 所在地：佩爾格(Perga或Perge)
簡介,發展,性質,橢圓,雙曲線,拋物線,離心率,極坐標方程,焦半徑,切線方程,焦準距,焦點三角形,通徑,對比,中點弦問題,統一方程,
簡介
圓錐曲線亦稱圓錐截線。簡稱錐線。一類重要的二次曲線。它是不過圓錐頂點的平面與圓錐面相交而成的曲線。
設圓錐的半頂角為α，平面與圓錐的軸所成的角為θ：
當θ=α 時，截面和圓錐的一條母線平行，交線是拋物線；
當 α<θ≤π/2 時，截面和所有的母線相交，交線是橢圓，特別當θ=π/2 時，交線時圓；
當 0≤θ<α 時，截面和兩條母線平行，交線時雙曲線。
因此，圓錐曲線包括拋物線、橢圓和雙曲線，統稱圓錐曲線。如果平面過圓錐的頂點，截面與圓錐面的交集有以下幾種情況：
當θ=α 時，平面與圓錐面相切於圓錐的一條母線，可視為退化拋物線；
當α<θ≤π/2 時，平面與圓錐面有惟一公共點（圓錐的頂點），可視為退化的橢圓；
當 0≤θ<α 時，平面與圓錐面相交於兩條母線，可視為退化雙曲線。
這些交集統稱為退化圓錐曲線。一般所謂的圓錐曲線，是指非退化的圓錐曲線。
在平面仿射坐標系中，圓錐曲線的方程都是二元二次方程，因此，圓錐曲線又稱為二次曲線。而且平面與任何二次曲面的交線總是二次曲線。例如，圓柱的斜截口即為橢圓。構想在圓錐的頂點 V 處放一點光源，圓在燈光下的陰影一般時圓錐形的，因此，圓錐曲線是圓在中心投影下，在不同平面上的射影。橢圓、拋物線、雙曲線與圓在中心投影下互變的規律性對於航空測量（高空照片的分析）和透視學研究具有重要意義。
發展
圓錐曲線最早是由古希臘學者梅內克謬斯(Menaechmus)進行系統研究的。
到了亞歷山大里亞時期，阿波羅尼奧斯(Apollonius,(P))在他的《圓錐曲線學》中指出同一圓錐的不同截口曲線可以是拋物線（齊曲線）、橢圓（虧曲線）和雙曲線（超曲線），並且研究了圓錐曲線的共軛直徑、切線和法線及其性質，也研究了圓錐曲線的極點和極線的性質。書中沒有談準線，但圓錐曲線是到定點（焦點）和到定直線（準線）的距離之比為常數（離心率）的點的軌跡，對此歐幾里得(Euclid)是知道的，並由帕普斯(Pappus,(A))述及且給出證明，這些對形成近代圓錐曲線的理論有著深遠的影響。
自從笛卡兒(Descartes,R.)引進坐標系以來，沃利斯(Wallis,J.)在他的《論圓錐曲線》中，為了闡明阿波羅尼奧斯的結果，把幾何條件轉化為代數條件，第一個證明了動點坐標x,y的二元二次方程與幾何里的圓錐曲線對應，並開始用方程的理論來研究曲線的性質。
16 —17 世紀，隨著機械工業的誕生和航海、建築、造船、採礦等事業的發達，推動了天文學和力學的發展。這時在天文學上發現行星的軌道是橢圓，力學上確定了拋射體的軌道是拋物線等。因此，有關圓錐曲線的深人研究也就成為迫切的需要了。
到了18 世紀,由於歐拉(Euler,L.)等多人的努力，圓錐曲線的現代理論才有了最終的結果。
性質
橢圓
文字語言定義：平面內一個動點到一個定點與一條定直線的距離之比是一個小於1的正常數e。平面內一個動點到兩個定點（焦點）的距離和等於定長2a的點的集合（設動點為P，兩個定點為F1和F2，則PF1+PF2=2a）。定點是橢圓的焦點，定直線是橢圓的準線，常數e是橢圓的離心率。
標準方程：
其中
，
。
其中，。
雙曲線
文字語言定義：平面內一個動點到一個定點與一條定直線的距離之比是一個大於1的常數e;平面內一個動點到兩個定點（焦點）的距離差等於定長2a的點的集合（設動點為P，兩個定點為F1和F2，則│PF1-PF2│=2a）定點是雙曲線的焦點，定直線是雙曲線的準線，常數e是雙曲線的離心率。
標準方程：
其中a>0，b>0，c2=a2+b2。
其中a>0，b>0，c2=a2+b2。
參數方程：x=asecθ；y=btanθ （θ為參數）。
拋物線
x=2pt2 ，
y=2pt (t為參數)，
t=1/tanθ（tanθ為曲線上點與坐標原點確定直線的斜率）特別地，t可等於0。
y=ax2+bx+c （開口方向為y軸，a≠0） x=ay2+by+c （開口方向為x軸，a≠0)。
離心率
這裡的參數e就是圓錐曲線的離心率，它不僅可以描述圓錐曲線的類型，也可以描述圓錐曲線的具體形狀，簡言之，離心率相同的圓錐曲線都是相似圖形。一個圓錐曲線，只要確定了離心率，形狀就確定了。特別的，因為拋物線的離心率都等於1，所以所有的拋物線都是相似圖形。
極坐標方程
1、在圓錐中，圓錐曲線極坐標方程可表示為：
其中l表示半徑，e表示離心率；
2、在平面坐標系中，圓錐曲線極坐標方程可表示為：
焦半徑
圓錐曲線上任意一點到焦點的距離稱為焦半徑。
圓錐曲線左右焦點為F1、F2，其上任意一點為P(x,y)，則焦半徑為：
|PF1|=a+ex(PF1>PF2)；
|PF2|=a-ex(PF2<PF1)。
P在左支，|PF1|=-a-ex，|PF2|=a-ex；
P在右支，|PF1|=a+ex，|PF2|=-a+ex；
P在下支，|PF1|= -a-ey，|PF2|=a-ey；
P在上支，|PF1|= a+ey，|PF2|=-a+ey。
|PF|=x+p/2。
切線方程
以
代替
，以
代替
；以
代替
，以
代替
焦準距
橢圓：
；
雙曲線：；
拋物線：p。
焦點三角形
橢圓或雙曲線上的一點與兩焦點所構成的三角形。
設F1、F2分別為橢圓或雙曲線的兩個焦點，P為橢圓或雙曲線上的一點且PF1F2能構成三角形。
若∠F1PF2=θ，則橢圓焦點三角形的面積為
；
雙曲線焦點三角形的面積為
。
通徑
圓錐曲線中，過焦點並垂直於軸的弦稱為通徑。
橢圓的通徑：
雙曲線的通徑：
拋物線的通徑：2p
對比
標準方程 | x2/a2+y2/b2=1 (a>b>0) | x2/a2-y2/b2=1 (a>0,b>0) | y2=2px (p>0) |
範圍 | x∈[-a,a] y∈[-b,b] | x∈(-∞，-a]∪[a,+∞) y∈R | x∈[0,+∞) y∈R |
關於x軸，y軸，原點對稱 | 關於x軸，y軸，原點對稱 | 關於x軸對稱 | |
頂點 | (a,0),(-a,0),(0,b),(0,-b) | (a,0),(-a,0) | (0,0) |
(c,0),(-c,0) 【其中c2=a2-b2】 | (c,0),(-c,0) 【其中c2=a2+b2】 | (p/2,0) | |
x=±a2/c | x=±a2/c | x=-p/2 | |
—————— | y=±(b/a)x | ————— | |
e=c/a,e∈（0,1) | e=c/a,e∈（1,+∞） | e=1 | |
∣PF1∣=a+ex ∣PF2∣=a-ex | ∣PF1∣=∣ex+a∣ ∣PF2∣=∣ex-a∣ | ∣PF∣=x+p/2 | |
p=b2/c | p=b2/c | p | |
2b2/a | 2b2/a | 2p | |
x=a·cosθ y=b·sinθ，θ為參數 | x=a·secθ y=b·tanθ，θ為參數 | x=2pt2 y=2pt,t為參數 | |
過圓錐曲線上一點 (x0,y0）的切線方程 | x0·x/a2+y0·y/b2=1 | x0x/a2-y0·y/b2=1 | y0·y=p(x+x0) |
y=kx±√(a2·k2+b2) | y=kx±√(a2·k2-b2) | y=kx+p/2k |
中點弦問題
已知圓錐曲線內一點為圓錐曲線的一弦中點，求該弦的方程：
用點斜式設出該弦的方程（斜率不存在的情況需要另外考慮），與圓錐曲線方程聯立求得關於x的一元二次方程和關於y的一元二次方程，由韋達定理得到兩根之和的表達式，再由中點坐標公式和兩根之和的具體數值，求出該弦的方程。
2、點差法（代點相減法）
設出弦的兩端點坐標(x1,y1)和(x2,y2)，代入圓錐曲線的方程，將得到的兩個方程相減，運用平方差公式得[(x1+x2)(x1-x2)]/a2+[(y1+y2)(y1-y2)/b2]=0
統一方程
平面直角坐標系內的任意圓錐曲線可用如下方程表示：
其中，α∈[0,2π)，p>0，e≥0。
④e=0時，表示點F(g,h)。
五點法求平面內圓錐曲線可以採用該統一方程。代入五組有序實數對，求出對應參數。
註：此方程不適用於圓錐曲線的其他退化形式，如圓等。
附：當e≠0時，F(g,h)對應準線方程：
