基本介紹
- 中文名:奧雷姆
- 國籍:法國
- 出生地:1320年
- 職業:數學家、自然哲學家
簡介,成長曆程,
簡介
奧雷姆的祖先是諾曼第人(Norman, 10世紀定居在法國塞納河口的諾曼人).他早年可能就學於巴黎大學的著名學者J.比里當(Buridan),受其思想影響頗深.1348年以後在納瓦拉學院(Callée de Navarre)學神學,13555—1356年取得神學碩士學位.奧雷姆曾在學院管理財務,後來成為學院的主要負責人,直到1361年12月辭職. 奧雷姆
奧雷姆
 奧雷姆
奧雷姆成長曆程
他和當時的皇太子[1364年繼承其父約翰二世(John Ⅱ)成為法國國王查理五世(Charles V,1364—1380年在位)]有交往.1356年,約翰二世被英軍俘虜,皇太子攝政.1359年奧雷姆曾以國王秘書的身分簽署檔案.1360年被委派到魯昂(Rouen)去為太子商談一筆貸款.1361年奧雷姆被任命為巴約(Bayeux)的副主教,但沒有赴任.1362年11月23日又被任命為魯昂的牧師,1363年2月10日改任巴黎的聖沙佩勒(Sainte—Chapelle)的牧師.一年後(1364年3月18日)升任魯昂總教堂教長.他居此要職直到1377年成為利雪的主教.不過他在1380年以前並未定居在利雪,而是奔波於魯昂與巴黎之間.
中世紀的學者多半是神職人員,他們有充分的閒暇來研究學問,生活有保障,又有更多的機會接觸各種典籍文獻.奧雷姆就是典型的代表.他還有一個優越的條件,即得到國王的支持.
查理五世於1364年即位,他十分重視學術研究,關心為政府服務的學者.奧雷姆受他委託,從1369年起,把亞里士多德(Aristotle)的多種著作由拉丁文譯為法文,其中有《倫理學》(Lelivre de ethiques d’Aristote, 1372)、《政治學》 (Le livre depolitique d’Aristote,1374)、《經濟學》(Livre de economiqued’Aristote)等.後世對於這些譯本評價很高,認為對法國語言文字的發展作出了重要貢獻.
奧雷姆一生的著作在30種以上,不過大部還是手稿,其中一部分直到近、現代才刊行於世.從這些作品可以看到,他是一個頗有辨別力的經院哲學家,常針對當時流行的學說進行論爭,和一些神學家、占星術家及說教者對立.
在數學方面,奧雷姆有兩項突破性的工作,一是為解析幾何的創立開闢了道路;二是引入非正整指數冪的概念.
解析幾何的先驅解析幾何建立於17世紀,但其中包含的思想則由來已久.它的發展大致經過三個步驟:(1)發明坐標制,用兩個數確定點的位置;(2)認識幾何與代數(或形與數)的對應關係;(3)作出函式y=f(x)的圖形.

第一步起源很早,古代的天文學家如中國的石申、希臘的希帕霍斯(Hipparchus)用經緯度表示恆星在天球上的位置,就是一種坐標制.坐標思想甚至還可以上溯到古埃及人劃分地面區域的辦法(文獻[9],Vol.2,p.316).阿波羅尼奧斯(Apollonius)在《圓錐曲線論》中更進一步引入了一種斜角坐標系.
數與形互相滲透也是古已有之.畢達哥拉斯(Pythagoras)早就注意到兩者的結合.歐幾里得(Euclid)的幾何代數學(用幾何的方法論述代數問題)是眾所周知的.中世紀的L.斐波那契(Fibonacci)也曾在《實用幾何》(Practica geometriae,1220)中用代數方法去解幾何問題.
奧雷姆的貢獻在於向第三步過渡.他的思想已接觸到在直角坐標系中用曲線表示函式的圖象,不過只著重討論了勻加速度物體的運動.
13—14世紀,亞里士多德的學說盛行於歐洲,但其謬誤也漸為人們所察覺.14世紀40年代前後,英國牛津大學默頓學院(Merton College)有一批邏輯及自然哲學家力圖建立正確的理論.其中有T.布雷德沃丁(Bradwardine,英國基督教會中心坎特伯雷的大主教)、R.斯溫內謝德(Swineshead)等.他們研究“形態的幅度” (latitude of forms),相當於現在所說的“質的強度”(intensity of qualities).所謂“質”,指的是具有某種強度(在物體的某一點上或在某一時刻)的性質,如熱、密度、速度等.他們考察物體從某一點到另一點或從某一時刻到另一時刻的質的強度變化.這種變化可能是均勻的,也可能是非均勻的.
他們已得到一些結果,如具有勻加速度的運動物體在給定時間t內所經過的路程,S等於用同樣時間以平均速度所經過的路程.平均速度就是初速v0與末速vt的算術平均值,也就是時間中點的速度,即
這一公式被稱為“默頓法則”(文獻[7],P.88,譯本P.118).
奧雷姆深知這些結果.他在1350—1360年間先後寫了好幾種著作,闡述他的觀點.如《形態的幅度》(Tractatus de latitudi-nibus formarum)、《均勻與非均勻強度》(Tractatus de unifor-mitate et difformitate intensionum)、《質量與運動的構型》(Tractatus de configurationibus qualitatum et motuum)等.
他的中心思想是用圖形來表示一個可變數的值,這個量依賴於另一個量.這可說是函式概念及函式圖示法的萌芽.他詳細分析了勻加速運動,用一條水平直線(相當於現在的橫坐標軸)表示時間(即時間坐標),直線上每一點代表一個時刻.每一個時刻對應著一個速度,該速度可用一條垂直於此點的線段來代表,其長度正比於速度的大小.用線段表示一種量是依照希臘人的習慣,速度隨著時間均勻地增大,因此線段的長度也均勻地增長,它的端點就構成一條直線.這直線和水平直線,再加上表示初速、末速的線段圍成一個梯形.如初速為0,則形成一個三角形OtA(如圖).
奧雷姆指出,三角形的面積等於物體在時間t內經過的路程.在時間中點M處的速度是末速度之半,即平均速度,三角形面積就等於以同樣的時間t為底,以平均速度為高的矩形面積.這個結論和默頓法則是一致的,也可以說是默頓法則的一個幾何說明.猜想他已有粗淺的積分思想,否則就很難理解他實際已使用了瞬時速度這個概念.
試將[0,t]用分點
0<t1<t2<…tk-1<tk<··<t3=t
等分為n個子區間.取出一個甚小的時間段Δt=tk-tk-1來看,它所對應的細長梯形的上、下底vk-1,vk 差不多相等,每一個都可以作為平均速度,再乘以Δt就得到梯形面積Sk的近似值.所有這些Sk的總和等於三角形面積,也就是物體走過的全程.奧雷姆並沒有明顯地表達上面的推理,但可能是他的思路.
他當時是錯用地理經緯度的術語來敘述圖示法的.經度(longitudines)相當於現在的橫坐標,緯度(latitudines)相當於縱坐標(前面意譯為幅度),垂直線段頂點所形成的直線稱為“頂點直線”(linea summitatis),相當於函式的曲線.可見坐標思想直接來自經緯度.
奧雷姆的學說在歐洲產生了廣泛的影響,它不但啟發笛卡兒在此基礎上創立了解析幾何,還給伽利略的力學研究提供了線索.伽利略注意到根據奧雷姆關於勻加速度的圖解可以推出“奇數定律”(law of odd numbers),從而得到他的著名勻加速度運動公式.
同前面一樣,用分點將時間段[0,t]等分為n個子區間,每個子區這就是“奇數定律”.注意到從1起連續n個奇數的和等於n2,即得三角形面積(路程):



這正是伽利略的公式.

奧雷姆也曾討論過非均勻變化的情形,例如圖象不是直線而是一個半圓.若改變比例係數,圖象便是半圓的拉長或壓縮,不過他並不知道這是橢圓.他還把“形態幅度”的思想推廣到三維甚至四維的情形.考慮一個平面區域,在其上每一點都豎立一根垂直線段以表示某種形態的幅度,於是線段端點和平面構成一個立體.他的著眼點是立體而不是端點形成的曲面,因此和二元函式圖象的概念是有差距的.他還進一步推廣到三元函式的情形,不過當時歐洲的數學水平尚未具備發展這種新思想的條件(文獻[8],p.49).
其他貢獻
奧雷姆另一項突破性的貢獻是引入非正整指數的概念及符號.分指數的概念在布雷德沃丁的書中已見端倪.他討論力(F)、阻力(R)與速度(v)間的關係時曾給出指數式(1328):
奧雷姆以此為出發點加以發揮,在《比例的比例》(De proportio-nibus Proportionum,約1360)中給出指數的運算規律,相當於現在的 xm·xn=xm+n,(xm)n=xmn.【註:m,n為指數】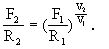
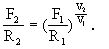
其中m,n可以是分數.在另一本書《比例算法》(Algorismusproportionum)中更創設分指數的符號.把
他也把在無窮級數方面,他已注意到斂散性的問題.並求出若干無窮級數的和.如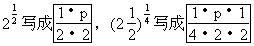


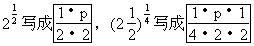


等.

除了數學之外,奧雷姆在別的領域也有不少論著.他的《占卜書》(Livre de divinacions)是為反對巫術和占星術而作.天文學方面,他在《球論》(Traité de la sphère)和《天空與世界認》(Livredu ciel et du monde)中闡發了他自己的宇宙觀.他不接受亞里士多德的靜止地球位於宇宙中心的學說,認為地球是動的,但未提出繞日的觀點.
奧雷姆曾從事財務管理及造幣工作,寫成《貨幣制度》(De moneta,約1360年寫成,1484年出版)一書.查理五世改革他的財政制度,就是以奧雷姆的理論為依據的.因此他又被稱為中世紀最大的經濟學家.
總之,奧雷姆在多方面特別是數學方面有許多創新,在中世紀的歐洲產生了深遠的影響.
