基本介紹
- 中文名:哈密頓函式
- 外文名:Hamiltonian function
- 別名:哈密爾頓運算元
- 學科:科學
- 英文縮寫:H
- 相關名詞:阿諾德函式
- 類型:科學術語
簡介
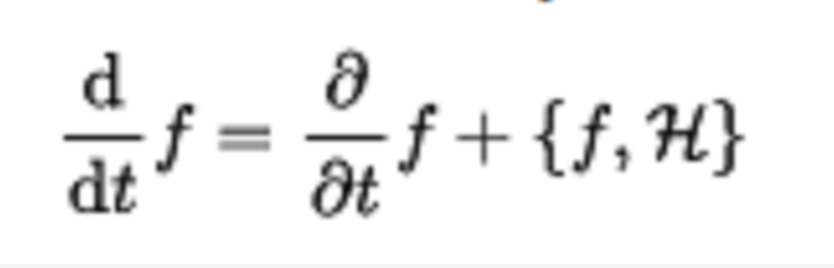
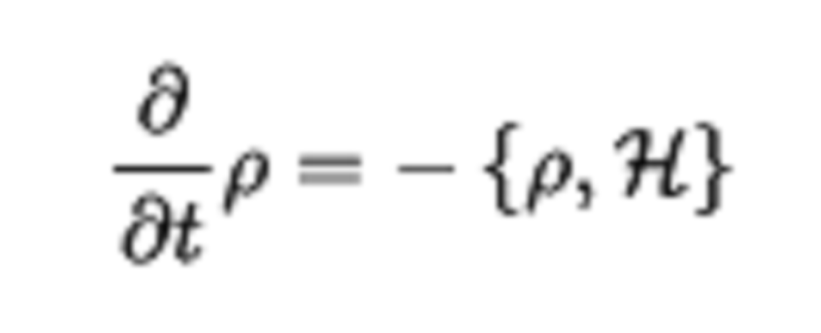
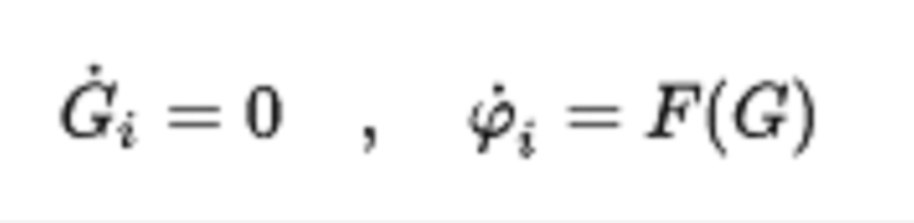
哈密爾頓函式一般指本詞條
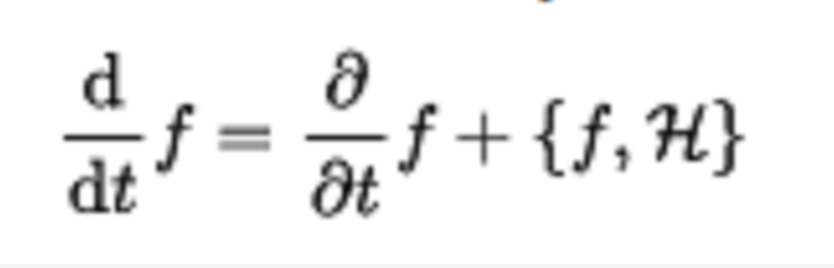
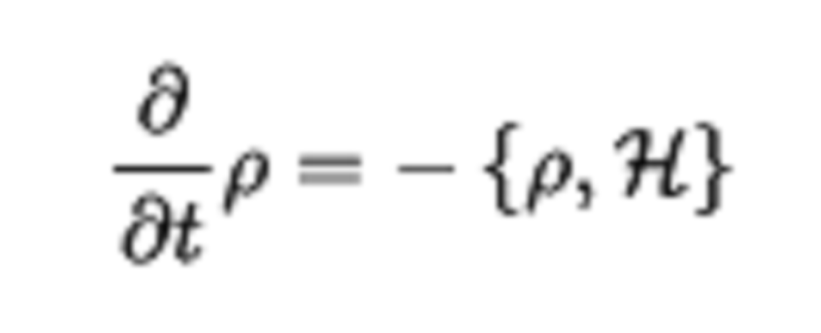
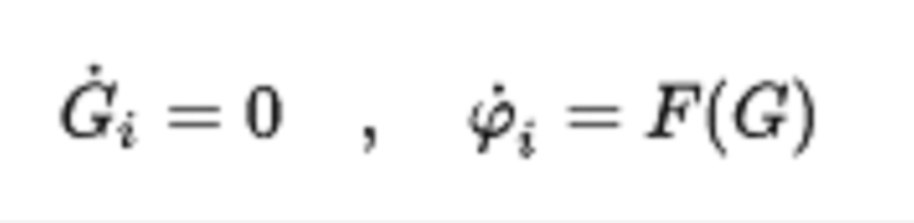
基於此,套用Hamilton函式方法,設計了系統的有限時間H無窮鎮定控制器,並將設計的控制器套用於非線性電路系統的控制設計中;3)將飽和輸入項表示為輸出反饋和死區非線性補償,在系統脈衝能控的條件下,套用嚴格系統等價方法和系統擴維技術...
是哈密頓量,未知函式 稱為哈密頓主函式, 是廣義坐標, 是積分常數,t是時間。假若能夠找到哈密頓主函式S的形式,就可以計算出廣義坐標 與廣義動量 隨時間的演變。這樣,可以完全地解析物理系統隨時間的演化。說明:矢量與標量分別...
哈密頓-雅可比-貝爾曼方程(Hamilton-Jacobi-Bellman equation,簡稱HJB方程)是一個偏微分方程,是最優控制的核心。HJB方程式的解是針對特定動態系統及相關代價函式下,有最小代價的實值函式。簡介 哈密頓-雅可比-貝爾曼方程(Hamilton-...
他還建立了與系統的總能量有關的哈密頓函式,這些工作推動了變分法和微分方程理論的進一步研究,在現代物理中得到廣泛套用。四元數 四元數使用於計算機圖形學、控制理論、信號處理、軌道力學,主要用於表示旋轉與方向。在代數中,二維複數...
其全部根都是其中一個根的有理函式,設x₁是n次阿貝爾方程的一個根,其全部根則為 ,其中Q(i=1,…,n-1)是有理函式,並且對於任意的1≤i≤j≤ n,有Q(Q(x₁))=Q(Q(x₁))。後人發現,阿貝爾方程是具有交換律的...
對於不同的勢函式 V,解這個偏微分方程的即得到定態波函式。哈密頓運算元 首先,“”這個東西具有“雙重性格”,它既是一個矢量,又是一個微分運算元(求導運算),所以哈密頓算符兼具矢量和微分的性質。按照定義:eg:其中 ,,分別為 ,...
一是在解析擾動下或僅勢能擾動下弱KAM解的攝動問題,以期得到預雙曲正定Hamilton系統連線軌道的解析通有性等;二是局部極小軌道與相關生成函式的問題,以期就正定哈密爾頓系統建立基於局部極小軌道而構造大範圍全局連線軌道的方法,從而有...
我們研究的對象為接觸哈密爾頓系統,其相應的接觸哈密爾頓函式為H(x, u, p),它與經典哈密爾頓系統(哈密爾頓函式H(x, u, p))之間的關係類似於辛幾何和接觸幾何之間的關係。接觸哈密爾頓系統是光學和波動問題的基礎,近來被廣泛運用於...
我們研究的對象為接觸哈密爾頓系統,其相應的接觸哈密爾頓函式為H(x, u, p),它與經典哈密爾頓系統(哈密爾頓函式H(x, u, p))之間的關係類似於辛幾何和接觸幾何之間的關係。接觸哈密爾頓系統是光學和波動問題的基礎。 我們的項目主要...
N a mathematical function of the coordinates and momenta of a system of particles used to express their equations of motion 哈密爾頓函式 ADJ denoting or relating to Sir William Rowan Hamilton, or to the theory of ...
哈密頓系統具有結構清晰、能夠提供系統及其控制行為的物理解釋、哈密頓函式為準Lyapunov 函式等優點。直線電機把電能直接轉換成直線運動,而不需要任何中間轉換機構的電磁傳動裝置,高精度直線電機伺服系統已成為伺服系統新的研究方向。本項目...
里茨方法是找到邊界值問題的近似解的直接方法。 該方法以瓦爾特·里茨命名。在量子力學中,粒子系統可以用“能量函式”或哈密爾頓運算元來描述,該能量函式將測量所提出的粒子構型的能量。 事實證明,某些特殊的組態比其他組態更可行,這與這個...
5.4 單機無窮大系統的能量函式的建立 5.5 基於哈密爾頓函式的勵磁控制器設計 5.6 利用能量函式整形設計勵磁控制器 5.7 直接補償機械阻尼係數的勵磁控制器的遞歸設計 5.8 發電機魯棒勵磁控制器的設計 5.8.1 基於哈密爾頓函式的...
可以在餘切叢上定義一組特殊的坐標系;這些被稱為標準坐標系。因為餘切叢可以視為辛流形,任何餘切叢上的實函式總是可以解釋為一個哈密爾頓函式;這樣餘切叢可以理解為哈密爾頓力學討論的相空間。利用切叢和餘切叢,可以得到(p,q)型張量...
可以在餘切叢上定義一組特殊的坐標系;這些被稱為標準坐標系。因為餘切叢可以視為辛流形,任何餘切叢上的實函式總是可以解釋為一個哈密爾頓函式;這樣餘切叢可以理解為哈密爾頓力學討論的相空間。切向量場 切向量場即切叢的截片,也常...
本書共六章,第一章結合實例分析最優控制問題的數學描述、系統性能指標等最優控制問題的相關研究內容並簡要介紹最優控制的發展過程;第二章討論函式的極值問題;第三章講述泛函與變分基本概念以及歐拉方程和橫截條件、哈密爾頓函式法等求解...
