基本介紹
- 中文名：里茨方法
- 外文名：Ritz method
- 學科：數學
- 提出者：瓦爾特·里茨
- 套用：計算哈密頓系統的和特徵值和向量
- 相關名詞：哈米爾頓算法
簡介,討論,與有限元法的關係,
簡介
里茨方法是找到邊界值問題的近似解的直接方法。 該方法以瓦爾特·里茨命名。
在量子力學中，粒子系統可以用“能量函式”或哈密爾頓運算元來描述，該能量函式將測量所提出的粒子構型的能量。 事實證明，某些特殊的組態比其他組態更可行，這與這個哈密頓系統的特徵分析（“特徵分析”）有關。 因為通常不可能分析所有的無限大的粒子組態以找到能量最少的粒子，為了數值計算的目的，能夠以某種方式近似這個哈密爾頓算法變得至關重要。
討論
與其他變分方法一樣，在系統上測試了一種試驗波函式ψ。 選擇此試驗功能以滿足邊界條件（以及任何其他物理限制）。具體功能未知； 試驗功能包含一個或多個可調整的參數，其可以變化以找到最低能量組態。
可以看出，基態能量E0滿足不等式：
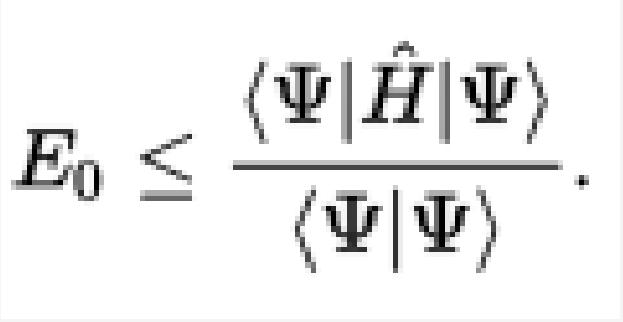
也就是說，基態能量小於該值。 試驗波函式將總是給出大於或等於地能的預期值。
如果已知測試波函式與基態正交，則它將為某些激發態的能量提供邊界。
里茨-ansatz函式是N個已知基函式的線性組合{ψi}，由未知係數參數：
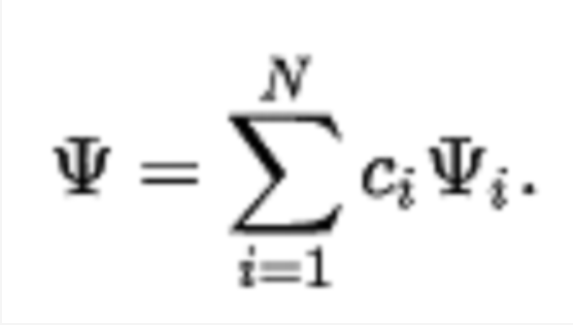
用一個已知的哈密爾頓運算元，我們可以寫出它的預期值
基函式通常不是正交的，因此重疊矩陣S具有非零非對角元素。{Ci}或{C*i}（第一個的共軛）可以用於最小化期望值。 例如，通過在{C*i}上製作
的偏導數，對於每個k = 1,2，...，N，獲得以下等式：
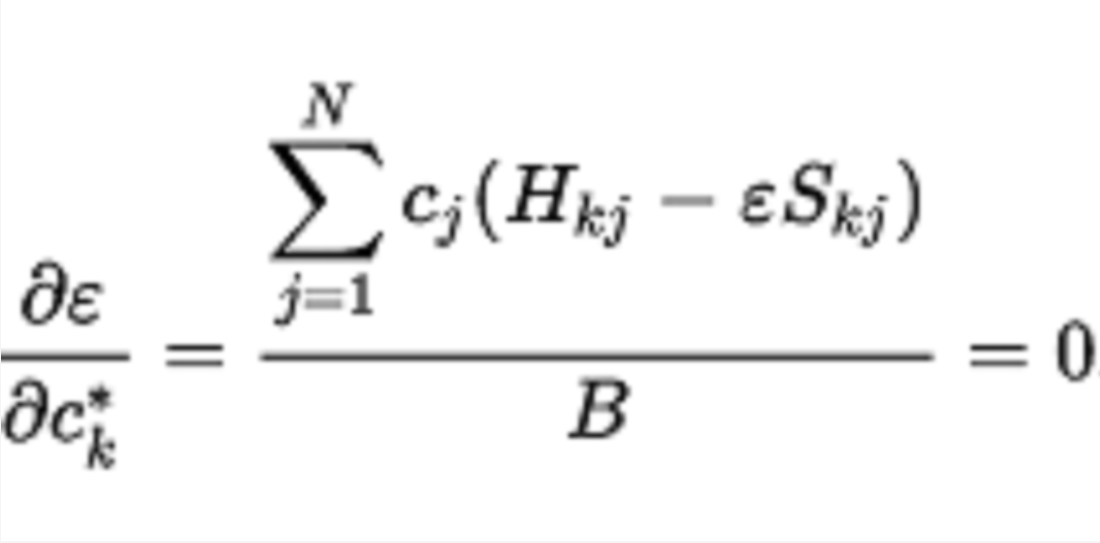
這形成了一組N個方程：
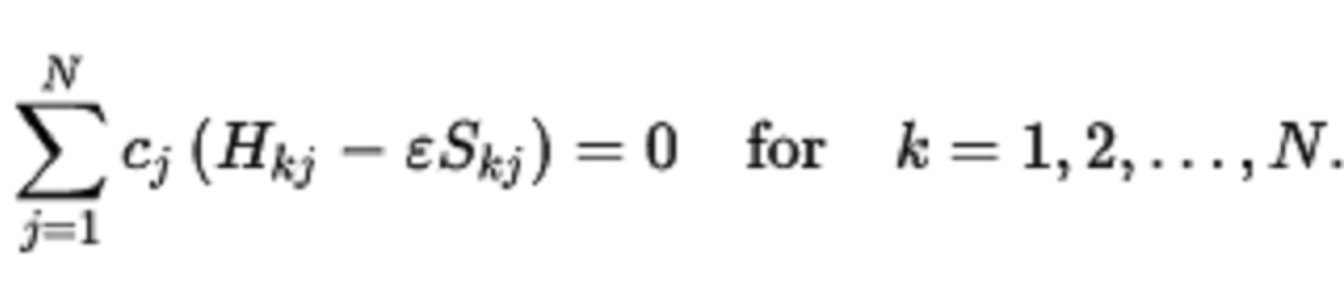
在上述等式中，能量和係數{Cj}是未知的。 關於c，這是一組均勻的線性方程，當這些未知數的係數的行列式為零時，它具有一個解：
而對於的N個值則反過來也是如此。 此外，由於哈密爾頓運算元是一個隱士運算元，因此H矩陣也是隱性的，並且i的值也是真實的。剩餘的N-1能量是激發態能量的估計。 通過從相應的方程中找到係數{Cj}可以獲得狀態i的波函式的近似值。
里茨方法(Rite method)變分問題的一種直接解法。設J<戶是待求函式y(x)的泛函，在C類函式中求使泛函J取得最小值的函式.給一個函式，J就有一值，對應於C類中所有函式，J有無窮多值。設d是這無窮個值所成集合的下確界，由下確界的定義，總能在C類中找到這樣的函式列{y} (x)，當n->}時J(yn)有有限極限d。這樣的函式列{y}(x)}就稱為極小化序列。
與有限元法的關係
