里茨-加廖金方法是求解數學物理方程的近似方法,主要用於橢圓型邊值問題。使方法具有極大的靈活適用性,能很好地處理複雜的幾何形狀、間斷介質以及奇性載荷等情況,在科學與工程的計算中獲得廣泛的使用。
基本介紹
- 中文名:里茨-加廖金方法
- 作用:主要用於橢圓型邊值問題
- 時間:1908年
- 提出者:W.里茨
正文,
正文
求解數學物理方程的近似方法,主要用於橢圓型邊值問題,W.里茨於1908年對此做了開創性的工作。這類方法從變分原理出發,選定有限個試探函式,,…,,用它們的線性組合構造近似解,從而把問題歸結為確定組合中的係數。
極小值原理 表達物理基本定律的一種形式,其表達可概括如下:給出一個依賴於物理狀態(為一函式)的變數()(數學上稱為泛函),同時給出()的容許函式集,即一切容許取的物理狀態,則真實的物理狀態就是中使()達到極小值的函式。例如彈性力學中著名的極小能量原理的表述是:彈性體在外力作用下的平衡位移使總勢能達到極小。這裡,總勢能是位移函式的泛函。現討論小變形的均勻彈性膜,膜在區域上的垂直位移用函式(,)表示,假定在邊界嬠上膜固定在坐標平面上,即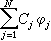 里茨-加廖金方法
里茨-加廖金方法
極小值原理 表達物理基本定律的一種形式,其表達可概括如下:給出一個依賴於物理狀態(為一函式)的變數()(數學上稱為泛函),同時給出()的容許函式集,即一切容許取的物理狀態,則真實的物理狀態就是中使()達到極小值的函式。例如彈性力學中著名的極小能量原理的表述是:彈性體在外力作用下的平衡位移使總勢能達到極小。這裡,總勢能是位移函式的泛函。現討論小變形的均勻彈性膜,膜在區域上的垂直位移用函式(,)表示,假定在邊界嬠上膜固定在坐標平面上,即
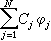 里茨-加廖金方法
里茨-加廖金方法, (1)
在外力(,)作用下彈性膜的總勢能為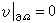 里茨-加廖金方法
里茨-加廖金方法
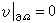 里茨-加廖金方法
里茨-加廖金方法(2)
它的容許函式集是滿足邊界條件(1)並使積分(2)存在的全體函式。由極小能量原理得出:彈性膜的平衡位移是中使總勢能(2)達到極小的函式,即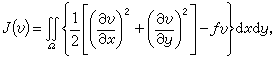 里茨-加廖金方法
里茨-加廖金方法
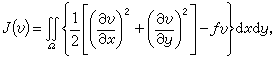 里茨-加廖金方法
里茨-加廖金方法。 (3)
虛功原理 又稱虛位移原理,在力學中與極小能量原理同屬變分原理。它的一般表述是:平衡系的力對虛位移所作的虛功為零。在彈性膜的例子中,如果仍以表示平衡位移,則虛功原理可表達為:對所有 υ∈,使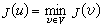 里茨-加廖金方法
里茨-加廖金方法
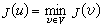 里茨-加廖金方法
里茨-加廖金方法(4)
成立。變分問題(3)或(4)確定的平衡位移,也是泊松方程第一邊值問題的解,即滿足
式中Δ為拉普拉斯運算元。
里茨法 從與微分方程問題等價的極小值原理出發,選擇有限個試探函式,,…,,在它們的線性組合中去找近似解。一般而言,試探函式須屬於容許函式集。把代入(2),得到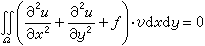 里茨-加廖金方法
里茨-加廖金方法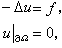 里茨-加廖金方法
里茨-加廖金方法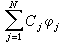 里茨-加廖金方法
里茨-加廖金方法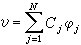 里茨-加廖金方法
里茨-加廖金方法
式中Δ為拉普拉斯運算元。
里茨法 從與微分方程問題等價的極小值原理出發,選擇有限個試探函式,,…,,在它們的線性組合中去找近似解。一般而言,試探函式須屬於容許函式集。把代入(2),得到
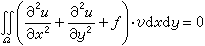 里茨-加廖金方法
里茨-加廖金方法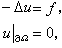 里茨-加廖金方法
里茨-加廖金方法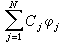 里茨-加廖金方法
里茨-加廖金方法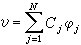 里茨-加廖金方法
里茨-加廖金方法(5)
式中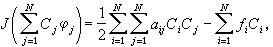 里茨-加廖金方法
里茨-加廖金方法
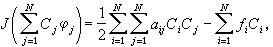 里茨-加廖金方法
里茨-加廖金方法,
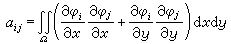 里茨-加廖金方法
里茨-加廖金方法。
由多元微分學可推出極小解的係數壣應滿足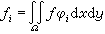 里茨-加廖金方法
里茨-加廖金方法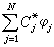 里茨-加廖金方法
里茨-加廖金方法
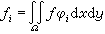 里茨-加廖金方法
里茨-加廖金方法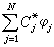 里茨-加廖金方法
里茨-加廖金方法(6)
故問題歸結為求解線代數方程組(6)。
加廖金法 從虛功方程(4)出發,把近似解表為試探函式,,…,的線性組合,另選定函式ψ,ψ,…,ψ作為(4)中的虛位移,ψ也須滿足邊界條件(1),稱為檢驗函式。將線性組合代入虛功方程(4),得到
利用分部積分公式得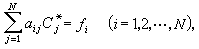 里茨-加廖金方法
里茨-加廖金方法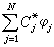 里茨-加廖金方法
里茨-加廖金方法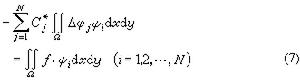 里茨-加廖金方法
里茨-加廖金方法
加廖金法 從虛功方程(4)出發,把近似解表為試探函式,,…,的線性組合,另選定函式ψ,ψ,…,ψ作為(4)中的虛位移,ψ也須滿足邊界條件(1),稱為檢驗函式。將線性組合代入虛功方程(4),得到
利用分部積分公式得
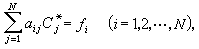 里茨-加廖金方法
里茨-加廖金方法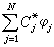 里茨-加廖金方法
里茨-加廖金方法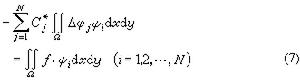 里茨-加廖金方法
里茨-加廖金方法。
若取ψ=,可看出方程組(7)即方程組(6),也就是說這時里茨法與加廖金法一致。由於檢驗函式ψ的選擇可不同於試驗函式,另外,對非自共軛問題=不存在等價的極小值問題,但可建立等價的廣義虛功方程
加廖金法仍可用,所以加廖金法是里茨法的推廣,它比里茨法更靈活和廣泛。
里茨-加廖金法的有效使用依賴於試探函式和檢驗函式的選取,傳統的做法是選取代數或三角多項式之類的解析函式,其優點是,對光滑解只需很少幾個,近似解就能達到很高的精度。在電子計算機出現之前,這種方法比較切合實際。但這樣選取的函式只當區域的形狀很特殊才能滿足給定的邊界條件,故在套用上受到很大限制。隨著電子計算機的出現,產生了有限元方法,它繼承了里茨-加廖金法從變分原理出發的基本特點,但不用多項式之類的解析函式,而是用剖分插值的方法構造試探函式和檢驗函式,從而使方法具有極大的靈活適用性,能很好地處理複雜的幾何形狀、間斷介質以及奇性載荷等情況,在科學與工程的計算中獲得廣泛的使用。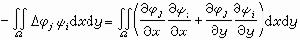 里茨-加廖金方法
里茨-加廖金方法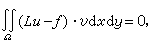 里茨-加廖金方法
里茨-加廖金方法
加廖金法仍可用,所以加廖金法是里茨法的推廣,它比里茨法更靈活和廣泛。
里茨-加廖金法的有效使用依賴於試探函式和檢驗函式的選取,傳統的做法是選取代數或三角多項式之類的解析函式,其優點是,對光滑解只需很少幾個,近似解就能達到很高的精度。在電子計算機出現之前,這種方法比較切合實際。但這樣選取的函式只當區域的形狀很特殊才能滿足給定的邊界條件,故在套用上受到很大限制。隨著電子計算機的出現,產生了有限元方法,它繼承了里茨-加廖金法從變分原理出發的基本特點,但不用多項式之類的解析函式,而是用剖分插值的方法構造試探函式和檢驗函式,從而使方法具有極大的靈活適用性,能很好地處理複雜的幾何形狀、間斷介質以及奇性載荷等情況,在科學與工程的計算中獲得廣泛的使用。
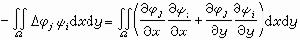 里茨-加廖金方法
里茨-加廖金方法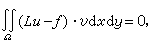 里茨-加廖金方法
里茨-加廖金方法