歷史,結構,輸入層,隱含層,輸出層,理論,學習範式,最佳化,加速,算法,一維算法,二維算法,性質,連線性,表征學習,生物學相似性,套用,計算機視覺,自然語言處理,其它,
歷史 對卷積神經網路的研究可追溯至日本學者福島邦彥(Kunihiko Fukushima)提出的neocognitron模型。在其1979和1980年發表的論文中,福島仿造生物的
視覺皮層 (visual cortex)設計了以“neocognitron”命名的神經網路。neocognitron是一個具有深度結構的神經網路,並且是最早被提出的深度學習算法之一,其隱含層由S層(Simple-layer)和C層(Complex-layer)交替構成。其中S層單元在
感受野 (receptive field)內對圖像特徵進行提取,C層單元接收和回響不同感受野返回的相同特徵。neocognitron的S層-C層組合能夠進行特徵提取和篩選,部分實現了卷積神經網路中
卷積層 (convolution layer)和池化層(pooling layer)的功能,被認為是啟發了卷積神經網路的開創性研究。
neocognition的構築與特徵可視化 第一個卷積神經網路是1987年由Alexander Waibel等提出的時間延遲網路(Time Delay Neural Network, TDNN)。TDNN是一個套用於語音識別問題的卷積神經網路,使用
FFT 預處理的語音信號作為輸入,其隱含層由2個一維卷積核組成,以提取頻率域上的平移不變特徵。由於在TDNN出現之前,人工智慧領域在
反向傳播算法 (Back-Propagation, BP)的研究中取得了突破性進展,因此TDNN得以使用BP框架內進行學習。在原作者的比較試驗中,TDNN的表現超過了同等條件下的
隱馬爾可夫模型 (Hidden Markov Model, HMM),而後者是二十世紀80年代語音識別的主流算法。
1988年,Wei Zhang提出了第一個二維卷積神經網路:平移不變人工神經網路(SIANN),並將其套用於檢測
醫學影像 。獨立於Zhang (1988),Yann LeCun在1989年同樣構建了套用於圖像分類的卷積神經網路,即LeNet的最初版本。LeNet包含兩個卷積層,2個全連線層,總計6萬個學習參數,規模遠超TDNN和SIANN,且在結構上與現代的卷積神經網路十分接近。LeCun (1989)對權重進行隨機初始化後使用了隨機梯度下降(Stochastic Gradient Descent, SGD)進行學習,這一策略被其後的深度學習研究廣泛採用。此外,LeCun (1989)在論述其網路結構時首次使用了“卷積”一詞,“卷積神經網路”也因此得名。
LeCun (1989)的工作在1993年由
貝爾實驗室 (AT&T Bell Laboratories)完成代碼開發並被大量部署於NCR(National Cash Register Coporation)的支票讀取系統。但總體而言,由於數值計算能力有限、學習樣本不足,加上同一時期以
支持向量機 (Support Vector Machine, SVM)為代表的核學習(kernel learning)方法的興起,這一時期為各類圖像處理問題設計的卷積神經網路停留在了研究階段,沒有得到廣泛套用。
在LeNet的基礎上,1998年Yann LeCun及其合作者構建了更加完備的卷積神經網路LeNet-5並在手寫數字的識別問題中取得成功。LeNet-5沿用了LeCun (1989) 的學習策略並在原有設計中加入了池化層對輸入特徵進行篩選。LeNet-5及其後產生的變體定義了現代卷積神經網路的基本結構,其構築中交替出現的卷積層-池化層被認為有效提取了輸入圖像的平移不變特徵。LeNet-5的成功使卷積神經網路的套用得到關注,微軟在2003年使用卷積神經網路開發了光學字元讀取(Optical Character Recognition, OCR)系統。其它基於卷積神經網路的套用研究也得到展開,包括
人像識別18 、
手勢識別19 等。
在2006年
深度學習 理論被正式提出後,卷積神經網路的表征學習能力得到了關注,並隨著數值計算設備的更新開始快速發展。自2012年的AlexNet開始,卷積神經網路多次成為
ImageNet 大規模視覺識別競賽(ImageNet Large Scale Visual Recognition Challenge, ILSVRC)的優勝算法,包括2013年的ZFNet、2014年的VGGNet、GoogLeNet和2015年的ResNet。
結構 輸入層 卷積神經網路的輸入層可以處理多維數據,常見地,一維卷積神經網路的輸入層接收一維或二維數組,其中一維數組通常為時間或頻譜採樣;二維數組可能包含多個通道;二維卷積神經網路的輸入層接收二維或三維數組;三維卷積神經網路的輸入層接收四維數組。由於卷積神經網路在
計算機視覺 領域有廣泛套用,因此許多研究在介紹其結構時預先假設了三維輸入數據,即平面上的二維像素點和
RGB 通道。
與其它神經網路算法類似,由於使用
梯度下降 進行學習,卷積神經網路的輸入特徵需要進行標準化處理。具體地,在將學習數據輸入卷積神經網路前,需在通道或時間/頻率維對輸入數據進行歸一化,若輸入數據為像素,也可將分布於
的原始像素值歸一化至
區間。輸入特徵的標準化有利於提升算法的運行效率和學習表現。
隱含層 卷積神經網路的隱含層包含
卷積層 、池化層和全連線層3類常見構築,在一些更為現代的算法中可能有Inception模組、殘差塊(residual block)等複雜構築。在常見構築中,卷積層和池化層為卷積神經網路特有。卷積層中的卷積核包含權重係數,而池化層不包含權重係數,因此在文獻中,池化層可能不被認為是獨立的層。以LeNet-5為例,3類常見構築在隱含層中的順序通常為:輸入-卷積層-池化層-卷積層-池化層-全連線層-輸出。
卷積層(convolutional layer)
1. 卷積核 (convolutional kernel) 卷積層的功能是對輸入數據進行特徵提取,其內部包含多個卷積核,組成卷積核的每個元素都對應一個權重係數和一個偏差量(bias vector),類似於一個前饋神經網路的神經元(neuron)。卷積層內每個神經元都與前一層中位置接近的區域的多個神經元相連,區域的大小取決於卷積核的大小,在文獻中被稱為“
感受野 (receptive field)”,其含義可類比
視覺皮層 細胞的感受野。卷積核在工作時,會有規律地掃過輸入特徵,在感受野內對輸入特徵做矩陣元素乘法求和併疊加偏差量:
式中的求和部分等價於求解一次
交叉相關 (cross-correlation)。
為偏差量,
和
表示第
層的卷積輸入和輸出,也被稱為特徵圖(feature map),
為
的尺寸,這裡假設特徵圖長寬相同。
對應特徵圖的像素,
為特徵圖的通道數,
、
和
是卷積層參數,對應卷積核大小、卷積步長(stride)和填充(padding)層數。
一維和二維卷積運算示例 上式以二維卷積核作為例子,一維或三維卷積核的工作方式與之類似。理論上卷積核也可以先翻轉180度,再求解交叉相關,其結果等價於滿足交換律的
線性卷積 (linear convolution),但這樣做在增加求解步驟的同時並不能為求解參數取得便利,因此線性卷積核使用交叉相關代替了卷積。
特殊地,當卷積核是大小
,步長
且不包含填充的單位卷積核時,卷積層內的交叉相關計算等價於矩陣乘法,並由此在卷積層間構建了全連線網路:
由單位卷積核組成的卷積層也被稱為網中網(Network-In-Network, NIN)或多層感知器卷積層(multilayer perceptron convolution layer, mlpconv)。單位卷積核可以在保持特徵圖尺寸的同時減少圖的通道數從而降低卷積層的計算量。完全由單位卷積核構建的卷積神經網路是一個包含參數共享的
多層感知器 (Muti-Layer Perceptron, MLP)。
線上性卷積的基礎上,一些卷積神經網路使用了更為複雜的卷積,包括平鋪卷積(tiled convolution)、
反卷積 (deconvolution)和擴張卷積(dilated convolution)。平鋪卷積的卷積核只掃過特徵圖的一部份,剩餘部分由同層的其它卷積核處理,因此卷積層間的參數僅被部分共享,有利於神經網路捕捉輸入圖像的旋轉不變(shift-invariant)特徵。
反卷積 或轉置卷積(transposed convolution)將單個的輸入激勵與多個輸出激勵相連線,對輸入圖像進行放大。由反卷積和向上池化層(up-pooling layer)構成的卷積神經網路在圖像語義分割(semantic segmentation)領域有重要套用,也被用於構建卷積自編碼器(Convolutional AutoEncoder, CAE)。擴張卷積線上性卷積的基礎上引入擴張率以提高卷積核的感受野,從而獲得特徵圖的更多信息,在面向序列數據使用時有利於捕捉學習目標的長距離依賴(long-range dependency)。使用擴張卷積的卷積神經網路主要被用於
自然語言處理 (Natrual Language Processing, NLP)領域,例如
機器翻譯31 、
語音識別32 等。
2. 卷積層參數
卷積層參數包括卷積核大小、步長和填充,三者共同決定了卷積層輸出特徵圖的尺寸,是卷積神經網路的超參數。其中卷積核大小可以指定為小於輸入圖像尺寸的任意值,卷積核越大,可提取的輸入特徵越複雜。
卷積核中RGB圖像的按0填充 卷積步長定義了卷積核相鄰兩次掃過特徵圖時位置的距離,卷積步長為1時,卷積核會逐個掃過特徵圖的元素,步長為n時會在下一次掃描跳過n-1個像素。
由卷積核的交叉相關計算可知,隨著卷積層的堆疊,特徵圖的尺寸會逐步減小,例如16×16的輸入圖像在經過單位步長、無填充的5×5的卷積核後,會輸出12×12的特徵圖。為此,填充是在特徵圖通過卷積核之前人為增大其尺寸以抵消計算中尺寸收縮影響的方法。常見的填充方法為按0填充和重複邊界值填充(replication padding)。填充依據其層數和目的可分為四類:
有效填充(valid padding):即完全不使用填充,卷積核只允許訪問特徵圖中包含完整感受野的位置。輸出的所有像素都是輸入中相同數量像素的函式。使用有效填充的卷積被稱為“窄卷積(narrow convolution)”,窄卷積輸出的特徵圖尺寸為(L-f)/s+1。
相同填充/半填充(same/half padding):只進行足夠的填充來保持輸出和輸入的特徵圖尺寸相同。相同填充下特徵圖的尺寸不會縮減但輸入像素中靠近邊界的部分相比於中間部分對於特徵圖的影響更小,即存在邊界像素的欠表達。使用相同填充的卷積被稱為“等長卷積(equal-width convolution)”。
全填充(full padding):進行足夠多的填充使得每個像素在每個方向上被訪問的次數相同。步長為1時,全填充輸出的特徵圖尺寸為L+f-1,大於輸入值。使用全填充的卷積被稱為“寬卷積(wide convolution)”
任意填充(arbitrary padding):介於有效填充和全填充之間,人為設定的填充,較少使用。
帶入先前的例子,若16×16的輸入圖像在經過單位步長的5×5的卷積核之前先進行相同填充,則會在水平和垂直方向填充兩層,即兩側各增加2個像素(
)變為20×20大小的圖像,通過卷積核後,輸出的特徵圖尺寸為16×16,保持了原本的尺寸。
3. 激勵函式 (activation function) 卷積層中包含激勵函式以協助表達複雜特徵,其表示形式如下:
類似於其它深度學習算法,卷積神經網路通常使用線性整流單元(Rectified Linear Unit, ReLU),其它類似ReLU的變體包括有斜率的ReLU(Leaky ReLU, LReLU)、參數化的ReLU(Parametric ReLU, PReLU)、隨機化的ReLU(Randomized ReLU, RReLU)、指數線性單元(Exponential Linear Unit, ELU)等。在ReLU出現以前,
Sigmoid函式 和
雙曲正切函式 (hyperbolic tangent)是常用的激勵函式。
激勵函式操作通常在卷積核之後,一些使用預激活(preactivation)技術的算法將激勵函式置於卷積核之前。在一些早期的卷積神經網路研究,例如LeNet-5中,激勵函式在池化層之後。
池化層(pooling layer)
在卷積層進行特徵提取後,輸出的特徵圖會被傳遞至池化層進行特徵選擇和信息過濾。池化層包含預設定的池化函式,其功能是將特徵圖中單個點的結果替換為其相鄰區域的特徵圖統計量。池化層選取池化區域與卷積核掃描特徵圖步驟相同,由池化大小、步長和填充控制。
1. Lp 池化( Lp pooling )
Lp 池化是一類受視覺皮層內階層結構啟發而建立的池化模型,其一般表示形式為:
式中步長
、像素
的含義與卷積層相同,
是預指定參數。當
時,L
p 池化在池化區域內取均值,被稱為均值池化(average pooling);當
時,L
p 池化在區域內取極大值,被稱為極大池化(max pooling)。均值池化和極大池化是最常見的池化方法,二者以損失特徵圖尺寸為代價保留圖像的背景和紋理信息。此外
時的L
2 池化在一些工作中也有使用。
2. 隨機/混合池化
混合池化(mixed pooling)和隨機池化(stochastic pooling)是L
p 池化概念的延伸。隨機池化會在其池化區域內按特定的機率分布隨機選取一值,以確保部分非極大的激勵信號能夠進入下一個構築。混合池化可以表示為均值池化和極大池化的
線性組合 :
有研究表明,混合池化和隨機池化有利於防止卷積神經網路的過度擬合,比均值和極大池化有更好的表現。
3. 譜池化(spectral pooling)
譜池化是基於FFT的池化方法,可以和FFT卷積一起被用於構建基於FFT的卷積神經網路。在給定特徵圖尺寸
,和池化層輸出尺寸時
,譜池化對特徵圖的每個通道分別進行DFT變換,並從頻譜中心截取n×n大小的序列進行DFT逆變換得到池化結果。譜池化有濾波功能,可以最大限度地保存低頻變化信息,並能有效控制特徵圖的大小。此外,基於成熟的FFT算法,譜池化能夠以很小的計算量完成。
Inception模組(Inception module)
Inception模組是對多個卷積層和池化層進行堆疊所得的特殊隱含層構築。具體而言,一個Inception模組會同時包含多個不同類型的卷積和池化操作,並使用相同填充使上述操作得到相同尺寸的特徵圖,隨後在數組中將這些特徵圖的通道進行疊加並通過激勵函式。由於上述做法在一個構築中引入了多個卷積計算,其計算量會顯著增大,因此為簡化計算量,Inception模組通常設計了瓶頸層,首先使用單位卷積核,即NIN結構減少特徵圖的通道數,再進行其它卷積操作。Inception模組最早被套用於GoogLeNet並取得了顯著的成功,也啟發了Xception算法中的深度可分卷積(depthwise separable convolution)思想。
Inception模組:原始版本(a),GoogLeNet使用的版本(b-d) 全連線層(fully-connected layer)
卷積神經網路中的全連線層等價於傳統前饋神經網路中的隱含層。全連線層通常搭建在卷積神經網路隱含層的最後部分,並只向其它全連線層傳遞信號。特徵圖在全連線層中會失去3維結構,被展開為向量並通過激勵函式傳遞至下一層。
在一些卷積神經網路中,全連線層的功能可部分由全局均值池化(global average pooling)取代,全局均值池化會將特徵圖每個通道的所有值取平均,即若有7×7×256的特徵圖,全局均值池化將返回一個256的向量,其中每個元素都是7×7,步長為7,無填充的均值池化。
輸出層 卷積神經網路中輸出層的上游通常是全連線層,因此其結構和工作原理與傳統前饋神經網路中的輸出層相同。對於圖像分類問題,輸出層使用邏輯函式或歸一化指數函式(softmax function)輸出分類標籤。在物體識別(object detection)問題中,輸出層可設計為輸出物體的中心坐標、大小和分類。在圖像語義分割中,輸出層直接輸出每個像素的分類結果。
理論 學習範式 監督學習(supervised learning)
卷積神經網路在監督學習中使用BP框架進行學習,其計算流程在LeCun (1989) 中就已經確定,是最早在BP框架進行學習的深度算法之一。卷積神經網路中的BP分為三部分,即全連線層與卷積核的反向傳播和池化層的反向通路(backward pass)。全連線層的BP計算與傳統的前饋神經網路相同,卷積層的反向傳播是一個與前向傳播類似的
交叉相關 計算:
式中
為
代價函式 (cost function)計算的誤差、
為
激勵函式 的
導數 、
是學習速率(learning rate),若卷積核的前向傳播使用卷積計算,則反向傳播也對卷積核翻轉以進行卷積運算。卷積神經網路的誤差函式可以有多種選擇,常見的包括Softmax損失函式(softmax loss)、鉸鏈損失函式(hinge loss)、三重損失函式(triplet loss)等。
池化層在反向傳播中沒有參數更新,因此只需要根據池化方法將誤差分配到特徵圖的合適位置即可,對極大池化,所有誤差會被賦予到極大值所在位置;對均值池化,誤差會平均分配到整個池化區域。
卷積神經網路通常使用BP框架內的隨機梯度下降(Stochastic Gradient Descent, SGD)和其變體,例如Adam算法(Adaptive moment estimation)。SGD在每次疊代中隨機選擇樣本計算
梯度 ,在大量學習樣本的情形下有利於信息篩選,在疊代初期能快速
收斂 ,且計算複雜度更小。
非監督學習(unsupervised learning)
卷積神經網路在監督學習問題下有廣泛套用,但也可以使用無標籤數據進行非監督學習。可用的方法包括卷積自編碼器(Convolutional AutoEncoders, CAE)、卷積受限玻爾茲曼機(Convolutional Restricted Boltzmann Machines, CRBM)/卷積深度置信網路(Convolutional Deep Belief Networks, CDBN)和深度卷積生成對抗網路(Deep Convolutional Generative Adversarial Networks, DCGAN)。這些算法也可以視為在非監督學習算法的原始版本中引入卷積神經網路構築的混合算法。
CAE的構建邏輯與傳統AE類似,首先使用卷積層和池化層建立常規的卷積神經網路作為編碼器,隨後使用反卷積和向上池化(up-pooling)作為解碼器,以樣本編碼前後的誤差進行學習,並輸出編碼器的編碼結果實現對樣本的維度消減(dimentionality reduction)和
聚類 (clustering)。在圖像識別問題,例如MNIST中,CAE與其編碼器同樣結構的卷積神經網路在大樣本時表現相當,但在小樣本問題中具有更好的識別效果。
CRBM是以卷積層作為隱含層的
受限玻爾茲曼機 (Boltzmann Machines, RBM),在傳統RBMs的基礎上將隱含層分為多個“組(group)”,每個組包含一個卷積核,卷積核參數由該組對應的所有二元節點共享。CDBN是以CRBM作為構築進行堆疊得到的階層式生成模型,為了在結構中提取高階特徵,CDBN加入了機率極大池化層( probabilistic max-pooling layer),和其對應的能量函式。CRBMs和CDBMs使用逐層貪婪算法(greedy layer-wise training)進行學習,並可以使用稀疏正則化(sparsity regularization)技術。在Caltech-101數據的物體識別問題中,一個24-100的兩層CDBN識別準確率持平或超過了很多包含高度特化特徵的分類和聚類算法。
生成對抗網路 ( Generative Adversarial Networks, GAN)可被用於卷積神經網路的非監督學習,DCGAN從一組機率分布,即潛空間(latent space)中隨機採樣,並將信號輸入一組完全由轉置卷積核組成的生成器;生成器生成圖像後輸入以卷積神經網路構成的判別模型,判別模型判斷生成圖像是否是真實的學習樣本。當生成模型能夠使判別模型無法判斷其生成圖像與學習樣本的區別時學習結束。研究表明DCGANs能夠在圖像處理問題中提取輸入圖像的重要特徵,在CIFAR-10數據的試驗中,對DCGAN判別模型的特徵進行處理後做為其它算法的輸入,能以很高的準確率對圖像進行分類。
最佳化 正則化 (regularization)
在神經網路算法的各類正則化方法都可以用於卷積神經網路以防止過度擬合,常見的正則化方法包括L
p 正則化(L
p -norm regularization)、
隨機失活 (spatial dropout)和隨機連線失活(drop connect)。
Lp 正則化在定義損失函式時加入隱含層參數以約束神經網路的複雜度:
式中
為損失函式,包含弗羅貝尼烏斯範數(Frobenius norm)的求和項被稱為正則化項,其中
是正則化參數,用以確定正則化項的約束力。可證明,當
時,正則化項是
凸函式 (convex function);特別地,當
時,L
2 正則化又被成為Tikhonov正則化(Tikhonov regularization)。
時的L
p 正則化有利於卷積核權重的稀疏化,但此時的正則化向不是凸函式。
卷積神經網路中的空間隨機失活(spatial dropout)是
前饋神經網路 中隨機失活理論的推廣。在全連線網路的學習中,隨機失活會隨機將神經元的輸出歸零,而空間隨機失活在疊代中會隨機選取特徵圖的通道使其歸零。進一步地,隨機連線失活直接作用於卷積核,在疊代中使卷積核的部分權重歸零。研究表明空間隨機失活和隨機連線失活提升了卷積神經網路的泛化能力,在
學習樣本 不足時效果顯著。
分批歸一化(Batch Normalization, BN)
數據的
標準化 是神經網路輸入管道中預處理的重要步驟。在深度網路中,隨著特徵在隱含層內的逐級傳遞,其均值和標準差會隨之改變,產生協變漂移(covariate shift)現象。協變漂移是深度網路發生梯度消失(vanishing gradient)的重要原因。BN以引入額外學習參數為代價部分解決了此類問題,其策略是在隱含層中首先將特徵標準化,然後使用兩個線性參數將標準化的特徵放大作為新的輸入,神經網路會在學習過程中更新其BN參數。卷積神經網路中的BN參數與卷積核參數具有相同的性質,即特徵圖中同一個通道的像素共享一組BN參數。此外使用BN時卷積層不需要偏差項,其功能由BN參數代替。
跳躍連線(skip connection) 包含跳躍連線的殘差塊 跳躍連線或短路連線(shortcut connection)來源於
循環神經網路 (Recurrent Neural Network, RNN)中的跳躍連線和各類門控算法,是解決深度網路中梯度消失問題的重要技術。卷積神經網路中的跳躍連線可以跨越任意數量的隱含層,這裡以相鄰隱含層間的跳躍進行說明:
式中
是特徵圖的轉換係數,當
和
的尺寸不同時,轉換係數將尺寸更小的特徵圖,通常是
轉換為
的尺寸,確保矩陣元素運算成立。當
的輸出值小而
的輸出值大時,卷積層
的輸出近似於
等值函式 ,對該層的特徵傳遞沒有負面影響,因此設定了
層的學習基線,使該層在疊代中至少不會退化。在BP框架內,部分誤差在反向傳播時可以跳過
層直接作用於
層,補償了其在深度結構中逐級傳播造成的梯度損失,因此有利於深度結構的誤差傳播。包含跳躍連線的多個卷積層的組合被稱為殘差塊(residual block),是現代卷積神經網路的重要構築技術。
加速 通用加速技術
卷積神經網路可以使用和其它深度學習算法類似的加速技術以提升運行效率,包括
量化 (quantization)、
遷移學習 (transfer learning)等。量化即在計算中使用低數值精度以提升計算速度,該技術在各類深度算法中被廣泛使用。對於卷積神經網路,一個極端的例子是XNOR-Net,即僅由
異或門 (XNOR)搭建的卷積神經網路。遷移學習一般性的策略是將非標籤數據遷移至標籤數據以提升神經網路的表現,卷積神經網路中遷移學習通常為使用在標籤數據下完成學習的卷積核權重初始化新的卷積神經網路,對非標籤數據進行遷移,或套用於其它標籤數據以縮短學習過程。
FFT 卷積
卷積神經網路的卷積和池化計算都可以通過
FFT 轉換至
頻率域 內進行,此時卷積核權重與BP算法中梯度的FFT能夠被重複利用,逆FFT也只需在輸出結果時使用,降低了計算複雜度。同時作為被廣泛使用的
數值計算 方法,一些數值計算庫包含了
GPU 設備的FFT,能提供進一步加速。FFT卷積在處理小尺寸的卷積核時可使用Winograd算法降低記憶體開銷。
權重稀疏化
在卷積神經網路中對權重進行稀疏化,能夠減少卷積核的冗餘,降低計算複雜度,使用該技術的構築被稱為稀疏卷積神經網路(Sparse Convolutional Neural Networks)。在對
ImageNet 數據的學習中,一個以90%比率稀疏化的卷積神經網路的運行速度是同結構傳統卷積神經網路的2至10倍,而輸出的分類精度僅損失了2%。
算法 一維算法 時間延遲網路(Time Delay Neural Network, TDNN)
TDNN是一類套用於語音識別問題的一維卷積神經網路,也是歷史上最早被提出的卷積神經網路算法之一。這裡以TDNN的原始版本Waibel et al. (1987)為例進行介紹。
TDNN構築示意圖 TDNN的學習目標為對FFT變換的3個語音音節/b,d,g/進行分類,其隱含層完全由單位步長,無填充的卷積層組成。在文獻中,TDNN的卷積核尺寸使用“延遲(delay)”表述,由尺寸為3的一維卷積核構成的隱含層被定義為“時間延遲為2的隱含層”,即感受野包含無延遲輸入和2個延遲輸入。在此基礎上,TDNN有兩個卷積層,時間延遲分別為2和4,神經網路中每個輸入信號與8個隱含層神經元相連。TDNN沒有全連線層,而是將尾端卷積層的輸出直接相加通過激勵函式得到分類結果。按原作,輸入TDNN的預處理數據為15個10毫秒採樣的樣本(frame),每個樣本包含16個通道參數(filterbank coefficients),此時TDNN的結構如下:
(3)×16×8的卷積層(步長為1,無填充,Sigmoid函式)
(5)×8×3的卷積層(步長為1,無填充,Sigmoid函式)
對9×3的特徵圖求和輸出
列表中數字的含義為:(卷積核尺寸)×卷積核通道(與輸入數據通道數相同)×卷積核個數。TDNN的輸出層和兩個卷積層均使用Sigmoid函式作為激勵函式。除上述原始版本外,TDNN的後續研究中出現了套用於字元識別和物體識別的算法,其工作方式是將空間在通道維度展開並使用時間上的一維卷積核,即時間延遲進行學習。
WaveNet
WaveNet是被用於語音建模的一維卷積神經網路,其特點是採用擴張卷積和跳躍連線提升了神經網路對長距離依賴的學習能力。WaveNet面向序列數據設計,其結構和常見的卷積神經網路有較大差異,這裡按Van Den Oord et al. (2016)做簡單介紹:
WaveNet構築示意圖 WaveNet以經過量化和獨熱編碼(one-hot encoding)的音頻作為輸入特徵,具體為一個包含採樣和通道的二維數組。輸入特徵在WaveNet中首先進入線性卷積核,得到的特徵圖會通過多個擴張卷積塊(dilated stack),每個擴張卷積塊包含一個過濾器(filter)和一個門(gate),兩者都是步長為1,相同填充的線性卷積核,但前者使用
雙曲正切函式 作為激勵函式,後者使用
Sigmoid函式 。特徵圖從過濾器和門輸出後會做矩陣元素乘法並通過由NIN構建的瓶頸層,所得結果的一部分會由跳躍連線直接輸出,另一部分與進入該擴張卷積塊前的特徵圖進行線性組合進入下一個構築。WaveNet的末端部分將跳躍連線和擴張卷積塊的所有輸出相加並通過兩個ReLU-NIN結構,最後由歸一化指數函式輸出結果並使用
交叉熵 作為損失函式進行
監督學習 。WaveNet是一個生成模型(generative model),其輸出為每個序列元素相對於其之前所有元素的條件機率,與輸入序列具有相同的維度:
WaveNet被證實能夠生成接近真實的英文、中文和德文語音。在經過算法和運行效率的改進後,自2017年11月起,WaveNet開始為谷歌的商業套用“谷歌助手(Google Assistant)”提供語音合成。
二維算法 LeNet-5
LeNet-5是一個套用於圖像分類問題的卷積神經網路,其學習目標是從一系列由32×32×1灰度圖像表示的手寫數字中,識別和區分0-9。LeNet-5的隱含層由2個卷積層、2個池化層構築和2個全連線層組成,按如下方式構建:
LeNet-5的構築與特徵可視化 (3×3)×1×6的卷積層(步長為1,無填充),2×2均值池化(步長為2,無填充),tanh激勵函式
(5×5)×6×16的卷積層(步長為1,無填充),2×2均值池化(步長為2,無填充),tanh激勵函式
2個全連線層,神經元數量為120和84
從現代
深度學習 的觀點來看,LeNet-5規模很小,但考慮LeCun et al. (1998)的數值計算條件,LeNet-5在該時期仍具有相當的複雜度。LeNet-5使用
雙曲正切函式 作為激勵函式,使用
均方差 (Mean Squared Error, MSE)作為
誤差函式 並對卷積操作進行了修改以減少計算開銷,這些設定在隨後的卷積神經網路算法中已被更最佳化的方法取代。在現代機器學習庫的範式下,LeNet-5是一個易於實現的算法,這裡提供一個使用
TensorFlow 和
Keras 的計算例子:
# 導入模組import numpy as npimport tensorflow as tffrom tensorflow import kerasimport matplotlib.pyplot as plt# 讀取MNIST數據mnist = keras.datasets.mnist(x_train, y_train),(x_test, y_test) = mnist.load_data()# 重構數據至4維(樣本,像素X,像素Y,通道)x_train=x_train.reshape(x_train.shape+(1,))x_test=x_test.reshape(x_test.shape+(1,))x_train, x_test = x_train/255.0, x_test/255.0# 數據標籤label_train = keras.utils.to_categorical(y_train, 10)label_test = keras.utils.to_categorical(y_test, 10)# LeNet-5構築model = keras.Sequential([ keras.layers.Conv2D(6, kernel_size=(3, 3), strides=(1, 1), activation='tanh', padding='valid'), keras.layers.AveragePooling2D(pool_size=(2, 2), strides=(2, 2), padding='valid'), keras.layers.Conv2D(16, kernel_size=(5, 5), strides=(1, 1), activation='tanh', padding='valid'), keras.layers.AveragePooling2D(pool_size=(2, 2), strides=(2, 2), padding='valid'), keras.layers.Flatten(), keras.layers.Dense(120, activation='tanh'), keras.layers.Dense(84, activation='tanh'), keras.layers.Dense(10, activation='softmax'), ])# 使用SGD編譯模型model.compile(loss=keras.losses.categorical_crossentropy, optimizer='SGD')# 學習30個紀元(可依據CPU計算力調整),使用20%數據交叉驗證records = model.fit(x_train, label_train, epochs=20, validation_split=0.2)# 預測y_pred = np.argmax(model.predict(x_test), axis=1)print("prediction accuracy: {}".format(sum(y_pred==y_test)/len(y_test)))# 繪製結果plt.plot(records.history['loss'],label='training set loss')plt.plot(records.history['val_loss'],label='validation set loss')plt.ylabel('categorical cross-entropy'); plt.xlabel('epoch')plt.legend() 該例子使用MNIST數據代替LeCun et al. (1998)的原始數據,使用
交叉熵 (categorical cross-entropy)作為損失函式。
ILSVRC中的優勝算法
ILSVRC為各類套用於計算機視覺的人工智慧算法提供了比較的平台,其中有多個卷積神經網路算法在圖像分類和物體識別任務中獲得優勝,包括AlexNet、ZFNet、VGGNet、GoogLeNet和ResNet,這些算法在ImageNet數據中展現了良好的學習性能,也是卷積神經網路發展中具有代表意義的算法。
對AlexNet、ZFNet的編程實現與LeNet-5類似,對VGGNet、GoogLeNet和ResNet的編程實現較為繁瑣,一些機器學習庫提供了完整的封裝模型和完成學習的權重,這裡提供一些使用
TensorFlow 和
Keras 的例子:
from tensorflow import kerasfrom keras import applications# load model and pre-trained weightsmodel_vgg16 = applications.VGG16(weights='imagenet', include_top=False)model_vgg19 = applications.VGG19(weights='imagenet', include_top=False)model_resnet = applications.ResNet50(weights='imagenet', include_top=False)model_googlenet = applications.InceptionV3(weights='imagenet', include_top=False) 1. AlexNet
AlexNet是2012年ILSVRC圖像分類和物體識別算法的優勝者,也是LetNet-5之後受到人工智慧領域關注的現代卷積神經網路算法。AlexNet的隱含層由5個卷積層、3個池化層和3個全連線層組成,按如下方式構建:
AlexNet構築示意圖 (11×11)×3×96的卷積層(步長為4,無填充,ReLU),3×3極大池化(步長為2、無填充),LRN
(5×5)×96×256的卷積層(步長為1,相同填充,ReLU),3×3極大池化(步長為2、無填充),LRN
(3×3)×256×384的卷積層(步長為1,相同填充,ReLU)
(3×3)×384×384的卷積層(步長為1,相同填充,ReLU)
(3×3)×384×256的卷積層(步長為1,相同填充,ReLU),3×3極大池化(步長為2、無填充)
3個全連線層,神經元數量為4096、4096和1000
AlexNet在卷積層中選擇ReLU作為
激勵函式 ,使用了隨機失活,和數據增強(data data augmentation)技術,這些策略在其後的卷積神經網路中被廣泛使用。AlexNet也是首個基於
GPU 進行學習的卷積神經網路,Krizhevsky (2012) 將AlexNet按結構分為兩部分,分別在兩塊GPU設備上運行。此外AlexNet的1-2部分使用了局部回響歸一化(local response normalization, LRN),在2014年後出現的卷積神經網路中,LRN已由分批歸一化取代。
2. ZFNet
ZFNet是2013年ILSVRC圖像分類算法的優勝者,其結構與AlexNet相近,僅將第一個卷積層的卷積核大小調整為7×7、步長減半:
(7×7)×3×96的卷積層(步長為2,無填充,ReLU),3×3極大池化(步長為2、無填充),LRN
(5×5)×96×256的卷積層(步長為1,相同填充,ReLU),3×3極大池化(步長為2、無填充),LRN
(3×3)×256×384的卷積層(步長為1,相同填充,ReLU)
(3×3)×384×384的卷積層(步長為1,相同填充,ReLU)
(3×3)×384×256的卷積層(步長為1,相同填充,ReLU),3×3極大池化(步長為2、無填充)
3個全連線層,神經元數量為4096、4096和1000
ZFNet對卷積神經網路的貢獻不在其構築本身,而在於其原作者通過
反卷積 考察了ZFNet內部的特徵提取細節,解釋了卷積神經網路的特徵傳遞規律,即由簡單的邊緣、夾角過渡至更為複雜的全局特徵。
3. VGGNet
VGGNet是
牛津大學 視覺幾何團隊(Visual Geometry Group, VGG)開發的一組卷積神經網路算法,包括VGG-11、VGG-11-LRN、VGG-13、VGG-16和VGG-19。其中VGG-16是2014年ILSVRC物體識別算法的優勝者,其規模是AlexNet的2倍以上並擁有規律的結構,這裡以VGG-16為例介紹其構築。VGG-16的隱含層由13個卷積層、3個全連線層和5個池化層組成,按如下方式構建:
VGGNet構築示意圖 (3×3)×3×64的卷積層(步長為1,相同填充,ReLU),(3×3)×64×64的卷積層(步長為1,相同填充,ReLU),2×2極大池化(步長為2、無填充)
(3×3)×64×128的卷積層(步長為1,相同填充,ReLU),(3×3)×128×128的卷積層(步長為1,相同填充,ReLU),2×2極大池化(步長為2、無填充)
(3×3)×128×256的卷積層(步長為1,相同填充,ReLU),(3×3)×256×256的卷積層(步長為1,相同填充,ReLU),(3×3)×256×256的卷積層(步長為1,相同填充,ReLU),2×2極大池化(步長為2、無填充)
(3×3)×256×512的卷積層(步長為1,相同填充,ReLU),(3×3)×512×512的卷積層(步長為1,相同填充,ReLU),(3×3)×512×512的卷積層(步長為1,相同填充,ReLU),2×2極大池化(步長為2、無填充)
(3×3)×512×512的卷積層(步長為1,相同填充,ReLU),(3×3)×512×512的卷積層(步長為1,相同填充,ReLU),(3×3)×512×512的卷積層(步長為1,相同填充,ReLU),2×2極大池化(步長為2、無填充)
3個全連線層,神經元數量為4096、4096和1000
VGGNet構築中僅使用3×3的卷積核並保持卷積層中輸出特徵圖尺寸不變,通道數加倍,池化層中輸出的特徵圖尺寸減半,簡化了神經網路的拓撲結構並取得了良好效果。
4. GoogLeNet
GoogLeNet是2014年ILSVRC圖像分類算法的優勝者,是首個以Inception模組進行堆疊形成的大規模卷積神經網路。GoogLeNet共有四個版本:Inception v1、Inception v2、Inception v3、Inception v4,這裡以Inception v1為例介紹。首先,Inception v1的Inception模組被分為四部分:
Inception v1構築示意圖 N1個(1×1)×C的卷積核
B3個(1×1)×C的卷積核(BN,ReLU),N3個(3×3)×96的卷積核(步長為1,相同填充,BN,ReLU)
B5個(1×1)×C的卷積核(BN,ReLU),N5個(5×5)×16的卷積核(步長為1,相同填充,BN,ReLU)
3×3的極大池化(步長為1,相同填充),Np個(1×1)×C的卷積核(BN,ReLU)
在此基礎上,對3通道的RGB圖像輸入,Inception v1按如下方式構建:
Inception v1中的Iception模組 (7×7)×3×64的卷積層(步長為2,無填充,BN,ReLU),3×3的極大池化(步長為2,相同填充),LRN
(3×3)×64×192的卷積層(步長為1,相同填充,BN,ReLU),LRN,3×3極大池化(步長為2,相同填充)
Inception模組(N1=64,B3=96,N3=128,B5=16,N5=32,Np=32)
Inception模組(N1=128,B3=128,N3=192,B5=32,N5=96,Np=64)
3×3極大池化(步長為2,相同填充)
Inception模組(N1=192,B3=96,N3=208,B5=16,N5=48,Np=64)
旁枝:5×5均值池化(步長為3,無填充)
Inception模組(N1=160,B3=112,N3=224,B5=24,N5=64,Np=64)
Inception模組(N1=128,B3=128,N3=256,B5=24,N5=64,Np=64)
Inception模組(N1=112,B3=144,N3=288,B5=32,N5=64,Np=64)
旁枝:5×5均值池化(步長為3,無填充)
Inception模組(N1=256,B3=160,N3=320,B5=32,N5=128,Np=128)
Inception模組(N1=384,B3=192,N3=384,B5=48,N5=128,Np=128)
全局均值池化,1個全連線層,神經元數量為1000,權重40%隨機失活
GoogLeNet中的Inception模組啟發了一些更為現代的算法,例如2017年提出的Xception。Inception v1的另一特色是其隱含層中的兩個旁枝輸出,旁枝和主幹的所有輸出會通過指數歸一化函式得到結果,對神經網路起正則化的作用。
5. 殘差神經網路(Residual Network, ResNet)
ResNet來自微軟的人工智慧團隊Microsoft Research,是2015年ILSVRC圖像分類和物體識別算法的優勝者,其表現超過了GoogLeNet的第三代版本Inception v3。ResNet是使用殘差塊建立的大規模卷積神經網路,其規模是AlexNet的20倍、VGG-16的8倍,在ResNet的原始版本中,其殘差塊由2個卷積層、1個跳躍連線、BN和激勵函式組成,ResNet的隱含層共包含16個殘差塊,按如下方式構建:
ResNet(上),同規模的普通CNN(中)和VGG-19(下)構築的比較 (7×7)×3×64的卷積層(步長為2,無填充,ReLU,BN),3×3的極大池化(步長為2,相同填充)
3個殘差塊:3×3×64×64卷積層(步長為1,無填充,ReLU,BN),3×3×64×64卷積層(步長為1,無填充)
1個殘差塊:3×3×64×128(步長為2,無填充,ReLU,BN),3×3×128×128(步長為1,無填充,ReLU,BN)
3個殘差塊:3×3×128×128(步長為1,無填充,ReLU,BN),3×3×128×128(步長為1,無填充,ReLU,BN)
1個殘差塊:3×3×128×256(步長為2,無填充,ReLU,BN),3×3×256×256(步長為1,無填充,ReLU,BN)
5個殘差塊:3×3×256×256(步長為1,無填充,ReLU,BN),3×3×256×256(步長為1,無填充,ReLU,BN)
1個殘差塊:3×3×256×512(步長為2,無填充,ReLU,BN),3×3×512×512(步長為1,無填充,ReLU,BN)
2個殘差塊:3×3×512×512(步長為1,無填充,ReLU,BN),3×3×512×512(步長為1,無填充,ReLU,BN)
全局均值池化,1個全連線層,神經元數量為1000
ResNet受到關注的原因是其在隱含層中通過跳躍連線構建的殘差塊。殘差塊的堆疊緩解了深度神經網路普遍出現的梯度消失(gradient vanishing)問題,被其後的諸多算法使用,包括GoogLeNet中的Inception v4。
在ResNet的基礎上諸多研究嘗試了改進算法,包括預激活ResNet(preactivation ResNet)、寬ResNet(wide ResNet)、隨機深度ResNets(Stochastic Depth ResNets, SDR)和RiR(ResNet in ResNet)等。預激活ResNet將激勵函式和BN計算置於卷積核之前以提升學習表現和更快的學習速度;寬ResNet使用更多通道的卷積核以提升原ResNet的“寬度”,並嘗試在構築中引入隨機失活等最佳化技術;SDR在學習中隨機使卷積層失活並用等值函式取代以達到正則化的效果;RiR使用包含跳躍連線和傳統卷積層的並行結構建立廣義殘差塊,對ResNet進行了推廣。上述改進算法都報告了比傳統ResNet更好的學習表現,但尚未在使用標準數據的大規模比較,例如ILSVRC中得到驗證。
性質 連線性 卷積神經網路中卷積層間的連線被稱為
稀疏連線 (sparse connection),即相比於
前饋神經網路 中的全連線,卷積層中的神經元僅與其相鄰層的部分,而非全部神經元相連。具體地,卷積神經網路第l層特徵圖中的任意一個像素(神經元)都僅是l-1層中卷積核所定義的
感受野 內的像素的線性組合。卷積神經網路的稀疏連線具有正則化的效果,提高了網路結構的穩定性和
泛化能力 ,避免過度擬合,同時,稀疏連線減少了權重參數的總量,有利於神經網路的快速學習,和在計算時減少記憶體開銷。
卷積神經網路中特徵圖同一通道內的所有像素共享一組卷積核權重係數,該性質被稱為權重共享(weight sharing)。權重共享將卷積神經網路和其它包含局部連線結構的神經網路相區分,後者雖然使用了稀疏連線,但不同連線的權重是不同的。權重共享和稀疏連線一樣,減少了卷積神經網路的參數總量,並具有正則化的效果。
在全連線網路視角下,卷積神經網路的稀疏連線和權重共享可以被視為兩個無限強的
先驗 (pirior),即一個隱含層神經元在其感受野之外的所有權重係數恆為0(但感受野可以在空間移動);且在一個通道內,所有神經元的權重係數相同。
表征學習 作為
深度學習 的代表算法,卷積神經網路具有
表征學習 能力,即能夠從輸入信息中提取高階特徵。具體地,卷積神經網路中的卷積層和池化層能夠回響輸入特徵的平移不變性,即能夠識別位於空間不同位置的相近特徵。能夠提取平移不變特徵是卷積神經網路在計算機視覺問題中得到套用的原因之一。
基於反卷積和向上池化的卷積神經網路特徵重構 平移不變特徵在卷積神經網路內部的傳遞具有一般性的規律。在圖像處理問題中,卷積神經網路前部的特徵圖通常會提取圖像中顯著的高頻和低頻特徵;隨後經過池化的特徵圖會顯示出輸入圖像的邊緣特徵(aliasing artifacts);當信號進入更深的隱含層後,其更一般、更完整的特徵會被提取。
反卷積 和反池化(un-pooling)可以對卷積神經網路的隱含層特徵進行可視化。一個成功的卷積神經網路中,傳遞至全連線層的特徵圖會包含與學習目標相同的特徵,例如圖像分類中各個類別的完整圖像。
生物學相似性 卷積神經網路中基於感受野設定的稀疏連線有明確對應的神經科學過程——視覺神經系統中
視覺皮層 (visual cortex)對
視覺空間 (visual space)的組織。視覺皮層細胞從視網膜上的光感受器接收信號,但單個視覺皮層細胞不會接收光感受器的所有信號,而是只接受其所支配的刺激區域,即感受野內的信號。只有感受野內的刺激才能夠激活該神經元。大量視覺皮層細胞通過系統地將感受野疊加完整接收視網膜傳遞的信號並建立視覺空間。事實上機器學習的“感受野”一詞即來自其對應的生物學研究。卷積神經網路中的權重共享的性質在生物學中沒有明確證據,但在對與大腦學習密切相關的目標傳播(target-propagation, TP)和反饋調整(feedback alignment, FA) 機制的研究中,權重共享顯著提升了學習效果。
套用 計算機視覺 圖像識別 (image classification)
卷積神經網路長期以來是
圖像識別 領域的核心算法之一,並在大量學習數據時有穩定的表現。對於一般的大規模圖像分類問題,卷積神經網路可用於構建階層分類器(hierarchical classifier),也可以在精細分類識別(fine-grained recognition)中用於提取圖像的判別特徵以供其它分類器進行學習。對於後者,特徵提取可以人為地將圖像的不同部分分別輸入卷積神經網路,也可以由卷積神經網路通過
非監督學習 自行提取。
基於卷積神經網路的鳥類識別 對於
字元檢測 (text detection)和
字元識別 (text recognition)/光學字元讀取,卷積神經網路被用於判斷輸入的圖像是否包含字元,並從中剪取有效的字元片斷。其中使用多個
歸一化指數函式 直接分類的卷積神經網路被用於谷歌街景圖像的門牌號識別、包含
條件隨機場 (Conditional Random Fields, CRF)圖模型的卷積神經網路可以識別圖像中的單詞,卷積神經網路與
循環神經網路 (Recurrent Neural Network, RNN)相結合可以分別從圖像中提取字元特徵和進行序列標註(sequence labelling)。
CNN-RNN的字元識別和序列標註 物體識別(object recognition)
卷積神經網路可以通過三類方法進行物體識別:滑動視窗(sliding window)、選擇性搜尋(selective search)和YOLO(You Only Look Once)。滑動視窗出現最早,並被用於手勢識別等問題,但由於計算量大,已經被後兩者淘汰。選擇性搜尋對應區域卷積神經網路(Region-based CNN),該算法首先通過一般性步驟判斷一個視窗是否可能有目標物體,並進一步將其輸入複雜的識別器中。YOLO算法將物體識別定義為對圖像中分割框內各目標出現機率的回歸問題,並對所有分割框使用同一個卷積神經網路輸出各個目標的機率,中心坐標和框的尺寸。基於卷積神經網路的物體識別已被套用於自動駕駛和交通實時監測系統。
此外,卷積神經網在圖像語義分割(semantic segmentation)、場景分類(scene labeling)和圖像顯著度檢測(Visual Saliency Detection)等問題中也有套用,其表現被證實超過了很多使用特徵工程的分類系統。
行為認知(action recognition)
在針對圖像的行為認知研究中,卷積神經網路提取的圖像特徵被廣泛套用於行為分類(action classification)。在視頻的行為認知問題中,卷積神經網路可以保持其二維結構並通過堆疊連續時間片段的特徵進行學習、建立沿時間軸變化的3D卷積神經網路、或者逐幀提取特徵並輸入
循環神經網路 ,三者在特定問題下都可以表現出良好的效果。
姿態估計 (pose estimation)
姿態估計 在圖像中將人的姿態用坐標的形式輸出,最早在姿態估計中使用的卷積神經網路是DeepPose,DeepPose的結構類似於AlexNet,以完整的圖片作為輸出,按
監督學習 的方式訓練並輸出坐標點。此外也有關於局部姿態估計的卷積神經網路套用研究。對於視頻數據,有研究使用滑動視窗的卷積神經網路進行逐幀的姿態估計。
神經風格轉換(neural style transfer) 神經風格轉換:內容(左下)、風格(左上)、輸出(右) 神經風格轉換是卷積神經網路的一項特殊套用,其功能是在給定的兩份圖像的基礎上創作第三份圖像,並使其內容和風格與給定的圖像儘可能地接近。神經風格轉換在本質上利用了圖像特徵在卷積神經網路內的傳播規律,並定義內容(content loss)和風格(style loss)的誤差函式進行學習。神經風格轉換除進行藝術創作外,也被用於照片的後處理。
自然語言處理 總體而言,由於受到視窗或卷積核尺寸的限制,無法很好地學習自然語言數據的長距離依賴和結構化語法特徵,卷積神經網路在
自然語言處理 (Natural Language Processing, NLP)中的套用要少於
循環神經網路 ,且在很多問題中會在循環神經網路的構架上進行設計,但也有一些卷積神經網路算法在多個NLP主題中取得成功。
在
語音處理 (speech processing)領域,卷積神經網路的表現被證實優於
隱馬爾可夫模型 (Hidden Markov Model, HMM)、
高斯混合模型 (Gaussian Mixture Model, GMM )和其它一些深度算法。有研究使用卷積神經網路和HMM的混合模型進行語音處理,模型使用了小的卷積核並將替池化層用全連線層代替以提升其學習能力。卷積神經網路也可用於
語音合成 (speech synthesis)和語言建模(language modeling),例如WaveNet使用卷積神經網路構建的生成模型輸出語音的條件機率,並採樣合成語音。卷積神經網路與長短記憶模型(Long Short Term Memory model, LSTM)相結合可以很好地對輸入句子進行補全。其它有關的工作包括genCNN、ByteNet等。
其它 物理學
卷積神經網路在包含
大數據 問題的
物理學 研究中有重要套用。在
高能物理學 中,卷積神經網路被用於
粒子對撞機 (particle colliders)輸出的噴流圖(jet image)的分析和特徵學習,有關研究包括
夸克 (quark)/
膠子 (gluon)分類、
W玻色子 (W boson)識別和中微子相互作用(neutrino interaction)研究等。卷積神經網路在
天體物理學 中也有套用,有研究使用卷積神經網路對
天文望遠鏡 圖像進行星系形態學(galaxy morphology)分析和提取星系模型(galactic model)參數。利用遷移學習技術,預訓練的卷積神經網路可以對
LIGO (Laser Interferometer Gravitational-wave Observatory)數據中的噪聲(glitch)進行檢測,為數據的預處理提供幫助。
使用CNN提取噴流圖特徵 遙感科學
卷積神經網路在
遙感科學 ,尤其是
衛星遙感 中有廣泛套用。在解析遙感圖像的幾何、紋理和空間分布特徵時,卷積神經網路在計算效率和分類準確度方面均有明顯優勢。依據遙感圖像的來源和目的,卷積神經網路被用於下墊面使用和類型改變(land use/land cover change) 研究以及物理量,例如海冰覆蓋率(sea-ice concentration)的遙感反演。此外卷積神經網路被廣泛用於遙感圖像的物體識別和圖像語義分割,後兩者是直接的計算機視覺問題,這裡不再贅述。
大氣科學
在
大氣科學 中,卷積神經網路被用於數值模式的
統計降尺度 (Statistical Downscaling, SD)和格點氣候數據的
極端天氣 檢測。在統計降尺度方面,由超解析度卷積神經網路( Super-Resolution CNN, SRCNN)堆疊的多層級的降尺度系統可以將插值到高解析度的原始氣象數據和高解析度的
數字高程模型 (Degital Elevation Model, DEM)作為輸入,並輸出高解析度的氣象數據,其準確率超過了傳統的空間分解誤差訂正(Bias Corrected Spatial Disaggregation, BCSD)方法。在極端天氣檢測方面,仿AlexNet結構的卷積神經網路在
監督學習 和
半監督學習 中被證實能以很高的準確度識別
氣候模式 輸出和再分析數據(reanalysis data)中的
熱帶氣旋 (tropical cyclones)、
大氣層河流 (atmospheric rivers)和
鋒面 (weather fronts)現象。
基於堆疊SRCNN的降尺度研究 包含卷積神經網路的編程模組
現代主流的機器學習庫和界面,包括
TensorFlow 、
Keras 、Thenao、Microsoft-CNTK等都可以運行卷積神經網路算法。此外一些商用數值計算軟體,例如MATLAB也有卷積神經網路的構建工具可用。
 neocognition的構築與特徵可視化
neocognition的構築與特徵可視化














 一維和二維卷積運算示例
一維和二維卷積運算示例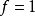


 卷積核中RGB圖像的按0填充
卷積核中RGB圖像的按0填充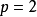
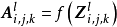
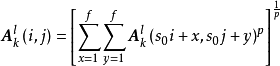






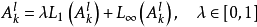


 Inception模組:原始版本(a),GoogLeNet使用的版本(b-d)
Inception模組:原始版本(a),GoogLeNet使用的版本(b-d)

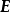





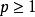
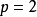

 包含跳躍連線的殘差塊
包含跳躍連線的殘差塊











 TDNN構築示意圖
TDNN構築示意圖 WaveNet構築示意圖
WaveNet構築示意圖
 LeNet-5的構築與特徵可視化
LeNet-5的構築與特徵可視化 AlexNet構築示意圖
AlexNet構築示意圖 VGGNet構築示意圖
VGGNet構築示意圖 Inception v1構築示意圖
Inception v1構築示意圖 Inception v1中的Iception模組
Inception v1中的Iception模組 ResNet(上),同規模的普通CNN(中)和VGG-19(下)構築的比較
ResNet(上),同規模的普通CNN(中)和VGG-19(下)構築的比較 基於反卷積和向上池化的卷積神經網路特徵重構
基於反卷積和向上池化的卷積神經網路特徵重構 基於卷積神經網路的鳥類識別
基於卷積神經網路的鳥類識別 CNN-RNN的字元識別和序列標註
CNN-RNN的字元識別和序列標註 神經風格轉換:內容(左下)、風格(左上)、輸出(右)
神經風格轉換:內容(左下)、風格(左上)、輸出(右) 使用CNN提取噴流圖特徵
使用CNN提取噴流圖特徵 基於堆疊SRCNN的降尺度研究
基於堆疊SRCNN的降尺度研究
