FFT(Fast Fourier Transformation)是離散傅氏變換(DFT)的快速算法。即為快速傅氏變換。它是根據離散傅氏變換的奇、偶、虛、實等特性,對離散傅立葉變換的算法進行改進獲得的。
基本介紹
- 中文名:快速傅氏變換
- 外文名:Fast Fourier Transformation
- 表達式:FFT
- 套用學科:數學
- 適用領域範圍:數位訊號處理
算法



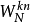
公式


源碼含義
//快速傅立葉變換// 入口參數:// l: l=0, 傅立葉變換;l=1, 逆傅立葉變換// il: il=0,不計算傅立葉變換或逆變換模和幅角;il=1,計算模和幅角// n: 輸入的點數,為偶數,一般為32,64,128,...,1024等// k: 滿足n=2^k(k>0),實質上k是n個採樣數據可以分解為偶次冪和奇次冪的次數// pr[]: l=0時,存放N點採樣數據的實部// l=1時, 存放傅立葉變換的N個實部// pi[]: l=0時,存放N點採樣數據的虛部// l=1時, 存放傅立葉變換的N個虛部//// 出口參數:// fr[]: l=0, 返回傅立葉變換的實部// l=1, 返回逆傅立葉變換的實部// fi[]: l=0, 返回傅立葉變換的虛部// l=1, 返回逆傅立葉變換的虛部// pr[]: il=1,i=0 時,返回傅立葉變換的模// il=1,i=1 時,返回逆傅立葉變換的模// pi[]: il=1,i=0 時,返回傅立葉變換的輻角// il=1,i=1 時,返回逆傅立葉變換的輻角void fft(double pr[], double pi[], int n, int k, double fr[], double fi[], int l, int il) { int it,m,is,i,j,nv,l0; double p,q,s,vr,vi,poddr,poddi; for(it=0; it<=n-1; m=it++) { is=0; for(i=0; i<=k-1; i++) { j=m/2; is=2*is+(m-2*j); m=j; } fr[it]=pr[is]; fi[it]=pi[is]; }//---------------------------- pr[0]=1.0; pi[0]=0.0; p=6.283185306/n; pr[1]=cos(p); pi[1]=-sin(p); if (l) pi[1]=-pi[1]; for(i=2; i<=n-1; i++) { p=pr[i-1]*pr[1]; q=pi[i-1]*pi[1]; s=(pr[i-1]+pi[i-1])*(pr[1]+pi[1]); pr=p-q; pi=s-p-q; } for(it=0; it<=n-2; it+=2) { vr=fr[it]; vi=fi[it]; fr[it]=vr+fr[it+1]; fi[it]=vi+fi[it+1]; fr[it+1]=vr-fr[it+1]; fi[it+1]=vi-fi[it+1]; } m=n/2; nv=2; for(l0=k-2; l0>=0; l0--) { m/=2; nv<<=1; for(it=0; it<=(m-1)*nv; it+=nv) for(j=0; j<=(nv/2)-1; j++) { p=pr[m*j]*fr[it+j+nv/2]; q=pi[m*j]*fi[it+j+nv/2]; s=pr[m*j]+pi[m*j]; s*=(fr[it+j+nv/2]+fi[it+j+nv/2]); poddr=p-q; poddi=s-p-q; fr[it+j+nv/2]=fr[it+j]-poddr; fi[it+j+nv/2]=fi[it+j]-poddi; fr[it+j]+=poddr; fi[it+j]+=poddi; } } if(l) for(i=0; i<=n-1; fr/=n,fi[i++]/=n); if(il) for(i=0; i<=n-1; i++) { pr=sqrt(fr*fr+fi*fi); if(fabs(fr)<0.000001*fabs(fi)) pi=fi*fr>0?90.0-90.0; else pi=atan(fi/fr)*360.0/6.283185306; } return;}// The following line must be defined before including math.h to correctly define M_PI#define _USE_MATH_DEFINES#include <math.h>#include <stdio.h>#include <stdlib.h>#define PI M_PI /* pi to machine precision, defined in math.h */#define TWOPI (2.0*PI)/*FFT/IFFT routine. (see pages 507-508 of Numerical Recipes in C)Inputs:data[] : array of complex* data points of size 2*NFFT+1.data[0] is unused,* the n'th complex number x(n), for 0 <= n <= length(x)-1, is stored as:data[2*n+1] = real(x(n))data[2*n+2] = imag(x(n))if length(Nx) < NFFT, the remainder of the array must be padded with zerosnn : FFT order NFFT. This MUST be a power of 2 and >= length(x).isign: if set to 1,computes the forward FFTif set to -1,computes Inverse FFT - in this case the output values haveto be manually normalized by multiplying with 1/NFFT.Outputs:data[] : The FFT or IFFT results are stored in data, overwriting the input.*/void four1(double data[], int nn, int isign) { int n, mmax, m, j, istep, i; double wtemp, wr, wpr, wpi, wi, theta; double tempr, tempi; n = nn << 1; j = 1; for (i = 1; i < n; i += 2) { if (j > i) { tempr = data[j]; data[j] = data[i]; data[i] = tempr; tempr = data[j+1]; data[j+1] = data[i+1]; data[i+1] = tempr; } m = n >> 1; while (m >= 2 && j > m) { j -= m; m >>= 1; } j += m; } mmax = 2; while (n > mmax) { istep = 2*mmax; theta = TWOPI/(isign*mmax); wtemp = sin(0.5*theta); wpr = -2.0*wtemp*wtemp; wpi = sin(theta); wr = 1.0; wi = 0.0; for (m = 1; m < mmax; m += 2) { for (i = m; i <= n; i += istep) { j =i + mmax; tempr = wr*data[j] - wi*data[j+1]; tempi = wr*data[j+1] + wi*data[j]; data[j] = data[i] - tempr; data[j+1] = data[i+1] - tempi; data[i] += tempr; data[i+1] += tempi; } wr = (wtemp = wr)*wpr - wi*wpi + wr; wi = wi*wpr + wtemp*wpi + wi; } mmax = istep; }}bool FFT(complex<double> * TD, complex<double> * FD, int r) {//一維快速Fourier變換。//complex<double> * TD ——指向時域數組的指針; complex<double> * FD ——指向頻域數組的指針; r ——2的冪數,即疊代次數 LONG count; // Fourier變換點數 int i,j,k; // 循環變數 int bfsize,p; // 中間變數 double angle; // 角度 complex<double> *W,*X1,*X2,*X; count = 1 << r; // 計算Fourier變換點數為1左移r位 W = new complex<double>[count / 2]; X1 = new complex<double>[count]; X2 = new complex<double>[count]; // 分配運算所需存儲器// 計算加權係數(旋轉因子w的i次冪表) for(i = 0; i < count / 2; i++) { angle = -i * PI * 2 / count; W[ i ] = complex<double> (cos(angle), sin(angle)); }// 將時域點寫入X1 memcpy(X1, TD, sizeof(complex<double>) * count);// 採用蝶形算法進行快速Fourier變換 for(k = 0; k < r; k++) { for(j = 0; j < 1 << k; j++) { bfsize = 1 << (r-k); for(i = 0; i < bfsize / 2; i++) { p = j * bfsize; X2[i + p] = X1[i + p] + X1[i + p + bfsize / 2] * W[i * (1<<k)]; X2[i + p + bfsize / 2] = X1[i + p] - X1[i + p + bfsize / 2] * W[i * (1<<k)]; } } X = X1; X1 = X2; X2 = X; }// 重新排序for(j = 0; j < count; j++) { p = 0; for(i = 0; i < r; i++) { if (j&(1<<i)) { p+=1<<(r-i-1); } } FD[j]=X1[p];}// 釋放記憶體delete W;delete X1;delete X2;return true;}使用方法
X=FFT(x);
X=FFT(x,N);
x=IFFT(X,N)
用MATLAB進行譜分析時注意:
(1)函式FFT返回值的數據結構具有對稱性。
例:
N=8;
n=0:N-1;
xn=[4 3 2 6 7 8 9 0];
Xk=fft(xn)
→
Xk =
Xk與xn的維數相同,共有8個元素。Xk的第一個數對應於直流分量,即頻率值為0。
(2)做FFT分析時,幅值大小與FFT選擇的點數有關,但不影響分析結果。在IFFT時已經做了處理。要得到真實的振幅值的大小,只要將得到的變換後結果乘以2除以N即可。
二.FFT套用舉例
例1:x=0.5*sin(2*pi*15*t)+2*sin(2*pi*40*t)。採樣頻率fs=100Hz,分別繪製N=128、1024點幅頻圖。
clf;
fs=100;N=128; %採樣頻率和數據點數
n=0:N-1;t=n/fs; %時間序列
x=0.5*sin(2*pi*15*t)+2*sin(2*pi*40*t); %信號
y=fft(x,N); %對信號進行快速Fourier變換
mag=abs(y); %求得Fourier變換後的振幅
f=n*fs/N; %頻率序列
subplot(2,2,1),plot(f,mag); %繪出隨頻率變化的振幅
xlabel('頻率/Hz');
ylabel('振幅');title('N=128');grid on;
subplot(2,2,2),plot(f(1:N/2),mag(1:N/2)); %繪出Nyquist頻率之前隨頻率變化的振幅
xlabel('頻率/Hz');
ylabel('振幅');title('N=128');grid on;
%對信號採樣數據為1024點的處理
fs=100;N=1024;n=0:N-1;t=n/fs;
x=0.5*sin(2*pi*15*t)+2*sin(2*pi*40*t); %信號
y=fft(x,N); %對信號進行快速Fourier變換
mag=abs(y); %求取Fourier變換的振幅
f=n*fs/N;
subplot(2,2,3),plot(f,mag); %繪出隨頻率變化的振幅
xlabel('頻率/Hz');
ylabel('振幅');title('N=1024');grid on;
subplot(2,2,4)
plot(f(1:N/2),mag(1:N/2)); %繪出Nyquist頻率之前隨頻率變化的振幅
xlabel('頻率/Hz');
ylabel('振幅');title('N=1024');grid on;
運行結果:
例2:x=0.5*sin(2*pi*15*t)+2*sin(2*pi*40*t),fs=100Hz,繪製:
(1)數據個數N=32,FFT所用的採樣點數NFFT=32;
(2)N=32,NFFT=128;
(3)N=136,NFFT=128;
(4)N=136,NFFT=512。
clf;fs=100; %採樣頻率
Ndata=32; %數據長度
N=32; %FFT的數據長度
n=0:Ndata-1;t=n/fs; %數據對應的時間序列
x=0.5*sin(2*pi*15*t)+2*sin(2*pi*40*t); %時間域信號
y=fft(x,N); %信號的Fourier變換
mag=abs(y); %求取振幅
f=(0:N-1)*fs/N; %真實頻率
subplot(2,2,1),plot(f(1:N/2),mag(1:N/2)*2/N); %繪出Nyquist頻率之前的振幅
xlabel('頻率/Hz');ylabel('振幅');
title('Ndata=32 Nfft=32');grid on;
N=128; %FFT採用的數據長度
n=0:Ndata-1;t=n/fs; %時間序列
x=0.5*sin(2*pi*15*t)+2*sin(2*pi*40*t);
y=fft(x,N);
mag=abs(y);
f=(0:N-1)*fs/N; %真實頻率
subplot(2,2,2),plot(f(1:N/2),mag(1:N/2)*2/N); %繪出Nyquist頻率之前的振幅
xlabel('頻率/Hz');ylabel('振幅');
title('Ndata=32 Nfft=128');grid on;
N=128; %FFT採用的數據個數
n=0:Ndata-1;t=n/fs; %時間序列
x=0.5*sin(2*pi*15*t)+2*sin(2*pi*40*t);
y=fft(x,N);
mag=abs(y);
f=(0:N-1)*fs/N; %真實頻率
subplot(2,2,3),plot(f(1:N/2),mag(1:N/2)*2/N); %繪出Nyquist頻率之前的振幅
xlabel('頻率/Hz');ylabel('振幅');
title('Ndata=136 Nfft=128');grid on;
N=512; %FFT所用的數據個數
n=0:Ndata-1;t=n/fs; %時間序列
x=0.5*sin(2*pi*15*t)+2*sin(2*pi*40*t);
y=fft(x,N);
mag=abs(y);
f=(0:N-1)*fs/N; %真實頻率
subplot(2,2,4),plot(f(1:N/2),mag(1:N/2)*2/N); %繪出Nyquist頻率之前的振幅
xlabel('頻率/Hz');ylabel('振幅');
title('Ndata=136 Nfft=512');grid on;
(1)當數據個數和FFT採用的數據個數均為32時,頻率解析度較低,但沒有由於添零而導致的其他頻率成分。
(2)由於在時間域內信號加零,致使振幅譜中出現很多其他成分,這是加零造成的。其振幅由於加了多個零而明顯減小。
(3)FFT程式將數據截斷,這時解析度較高。
(4)也是在數據的末尾補零,但由於含有信號的數據個數足夠多,FFT振幅譜也基本不受影響。
對信號進行頻譜分析時,數據樣本應有足夠的長度,一般FFT程式中所用數據點數與原含有信號數據點數相同,這樣的頻譜圖具有較高的質量,可減小因補零或截斷而產生的影響。
(2)中間的圖是將x(n)補90個零,幅度頻譜的數據相當密,稱為高密度頻譜圖。但從圖中很難看出信號的頻譜成分。
(3)信號的有效數據很長,可以清楚地看出信號的頻率成分,一個是0.24Hz,一個是0.26Hz,稱為高解析度頻譜。
可見,採樣數據過少,運用FFT變換不能分辨出其中的頻率成分。添加零後可增加頻譜中的數據個數,譜的密度增高了,但仍不能分辨其中的頻率成分,即譜的解析度沒有提高。只有數據點數足夠多時才能分辨其中的頻率成分。
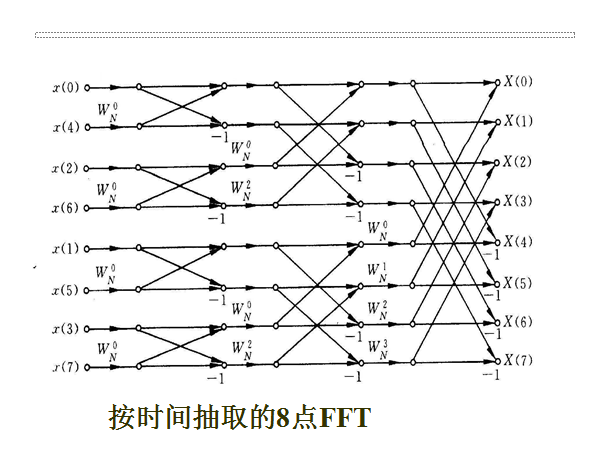
 FFT算法圖(Butterfly算法)
FFT算法圖(Butterfly算法)