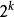威諾格拉德快速傅立葉算法（英語：Winograd FFT）是由美國計算機科學家Shmuel Winograd在1978年提出。此算法可以找出最少的乘法運算量。
基本介紹
- 中文名：威諾格拉德快速傅立葉變換
- 外文名：Winograd FFT
- 提出者：Shmuel Winograd
- 提出時間：1978
定義,使用方法,缺點,其他運用,
定義
當把DFT的公式：
用矩陣方式來表示：
如果n是質數，則可以無視第一行與第一列，把n點的DFT用n-1點的迴旋折積來取代。
使用方法
使用此算法，可分為以下幾個步驟，此處以n=5的DFT為例：
Step 1：消去第一行與第一列，式子可以改寫如下：
Step 2：找出列與行的順序：
a)找出一個原根a，使得
.
b)用p[n]表示列與行的順序：
在這例子中，N=5有兩個原根：2與3。取2作為其原根，可得其順序為：1,2,4,3。
故要將此矩陣
如此第一行與第一列都跟所求得的順序：1,2,4,3一樣，此為circular correlation的形式。
Step 3：為了要符合迴旋折積的定義(矩陣的對角線的項數相同)，故必須再將第二列與第四列交換，第二行與第四行交換，矩陣如下：
如此就可把N點DFT用N-1點的DFT來簡化，表示如下：
缺點
雖然此算法有著可以大幅減少乘法量的優點，但相對於此，也有一些缺點：
- N不同，那硬體的架構也會跟著改變。
- Time Cycle較多（因為要做兩次N-1點的DFT）。
- 加法量會增加很多。
其他運用
任意長度的DFT都可以用長度為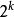
點的DFT來簡化，舉例來說：
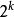
7點的DFT：先將7點DFT用Winograd簡化成6點DFT，再利用6=2x3，故6點DFT可用2點DFT與3點的DFT來表示，再把3點的DFT用Winograd簡化成2點的DFT，即可把7點的DFT用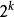
點的DFT來簡化。
