對於函式f(x)與g(x),若存在區間[m,n](m<n),使得f(x)與g(x)在區間[m,n]上的值域相等,則稱f(x)與g(x)為等值函式。
基本介紹
- 中文名:等值函式
- 外文名:Equivalent function
定義
等值函式的法向量
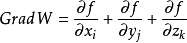

實例
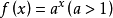

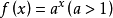

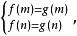

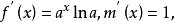
 f(x)、g(x)函式圖
f(x)、g(x)函式圖

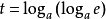
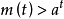
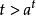



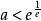

對於函式f(x)與g(x),若存在區間[m,n](m<n),使得f(x)與g(x)在區間[m,n]上的值域相等,則稱f(x)與g(x)為等值函式。
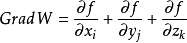

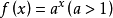

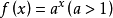

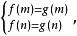

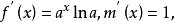
 f(x)、g(x)函式圖
f(x)、g(x)函式圖

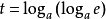
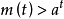
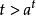



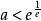

對於函式f(x)與g(x),若存在區間[m,n](m<n),使得f(x)與g(x)在區間[m,n]上的值域相等,則稱f(x)與g(x)為等值函式。...
目標函式f(x)就是用設計變數來表示的所追求的目標形式,所以目標函式就是設計變數的函式,是一個標量。從工程意義講,目標函式是系統的性能標準,比如,一個結構的最...
所謂等值面是指空間中的一個曲面,在該曲面上函式F(x, y, z)的值等於某一給定值Ft,即等值面是由所有點S = {(x, y, z):F(x, y, z) = Ft}組成...
等值集(level set)亦稱水平集,是等高線、等高面的數學抽象,設函式f:A→R,A⊆Rn,對於常數c,集合{x∈A|f(x)=c}稱為f的c等值集,簡稱等值集,當n=2或3...
位置函式等值線(isopleth of position function)海洋測繪中確定動點位置的一種方法.是指平面上位置函式為常數時動點的軌跡.在海洋測繪中,通常要求至少以兩條位置函式...
期望效用函式理論(Expected Utility Theory), 期望效用函式理論是20世紀50年代,馮·諾依曼和摩根斯坦(Von Neumann and Morgenstern)在公理化假設的基礎上,運用邏輯和...
一種擴展的新型數學函式。函式是數學中最難的,套用廣泛... 由於變值函式與基值函式同源共生,而等值函式只是變值函式和基值函式的一種特例,故三種函式具有本質上...
流體力學中的其中一個比較重要的函式叫流函式。流函式的等值線即是等流函式線。... 流體力學中的其中一個比較重要的函式叫流函式。流函式的等值線即是等流函式...
設函式f(x)的定義域為D,值域為B,如果存在函式x=g(t),使得函式y=f(g(t))的值域仍然是B,那么,稱函式x=g(t)是函式f(x)的一個等值域變換. ...
標量場是指一個僅用其大小就可以完整表征的場。一個標量場u 可以用一個標量函式u(x,y,z)來表示。標量場分為實標量場和復標量場,其中實標量場是最簡單的場...
變值係數可為首項為一任意非0常數的連續型初等函式(CS法常取首項為1的整式多項式),其中,首項(KA)對應於方箱體或等值部分,餘項(R)對應於變值部分。當變值...
