等值集

等值集(level set)亦稱水平集，是等高線、等高面的數學抽象，設函式f：A→R，A⊆Rⁿ，對於常數c，集合{x∈A|f(x)=c}稱為f的c等值集，簡稱等值集，當n=2或3時，等值集常常是曲線或曲面，稱為等值線(又稱等高線)或等值面(又稱等高面)，例如，構想f(x)為R³中的溫度場，則等值面就是等溫面，等值集常用於研究多元特別是二元實值函式的圖象。

基本介紹

• 中文名：等值集
• 外文名：level set
• 所屬學科：數學
• 別稱：水平集，c等值集
• 套用：研究多元特別是二元函式的圖象
• 簡介：等高線、等高面的數學抽象

基本介紹

設f(P)為一函式，c為其值域內的一個數，集合{P|f(P)=c}稱為此函式的c等值集。對不同的c，相應有不同的c等值集。

若P是二維的，則c等值集為{(x,y)|f(x,y)=c)，一般說來，它是一條曲線。

若P是三維的，則c等值集為{(x,y,z)|f(x,y,z)=c)，一般說來，它是一個曲面。

若P是更高維的，則c等值集就沒有直觀意義。

c等值集可以幫助我們了解f(P)隨P而變的情況。

例題解析

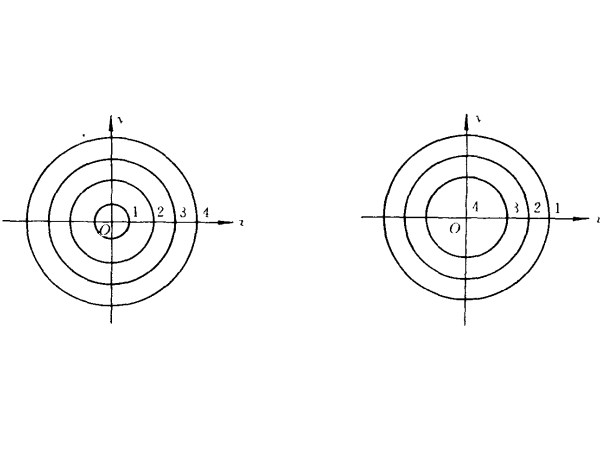
【例1】設為已給函式f(P)。

為其4—等值集，它是個圓；

為其3—等值集，它是個圓；

為其2—等值集，它是個圓；

為其1—等值集，它是個圓。

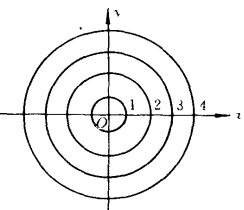從這些等值集可見當增加時，f(P)也增加f(P)之圖像一個茶杯(圖1)。

圖1

【例2】設為已給函式。

為其1—等值集，它是個圓；

為其2—等值集，它是個圓；

為其3—等值集，它是個圓；

為其4—等值集，它是個點圓。

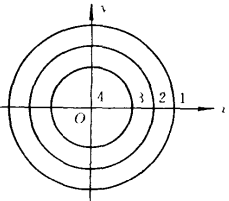從這些等值集可見當減小時f(P)增加，f(P)的圖象像一頂草帽(圖2)。

圖2

【例3】 的k等值集是=k。它是一個以(a，b，c)為球心，為半徑的球面。球越大，函式值也越大。

從這個例子可見，即使我們不能畫出函式的圖象，但還是可以通過等值集大致地看出函式值的改變情況。

f(x,y,z)的k等值集是{(x,y,z)|f(x,y,z)=k}。如記f(x,y,z)-k為F(x,y,z)，則此等值集即{(x,y,z)|F(x,y,z)=0}不管什麼F(x,y,z)=0，這種集合也叫做F(x,y,z)=0的圖象而F(x,y,z)=0則叫這圖象的方程。