在數學中,勒讓德函式Pλ,Qλ和相關的勒讓德函式Pλ,Qλ是勒讓德多項式與非整數度的泛化。
基本介紹
- 中文名:勒讓德函式
- 外文名:Legendre function
- 所屬學科:數學
- 實質:勒讓德多項式與非整數度的泛化
- 字母表示:Pλ,Qλ
- 相關名詞:伽馬函式
簡介
微分方程
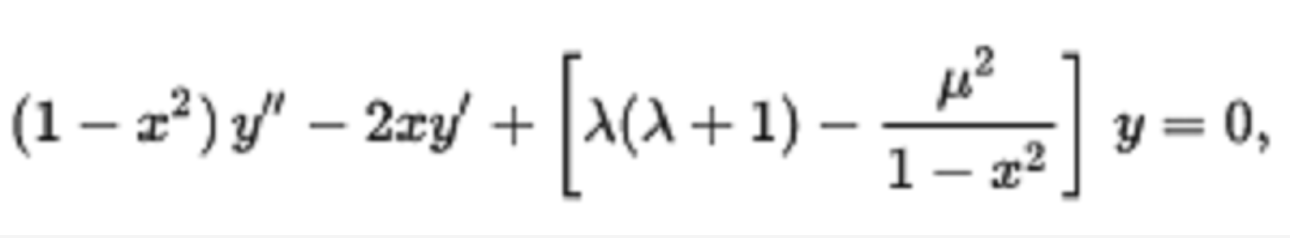
公式

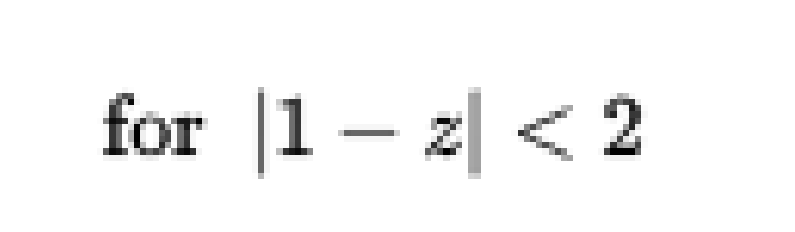
積分表示
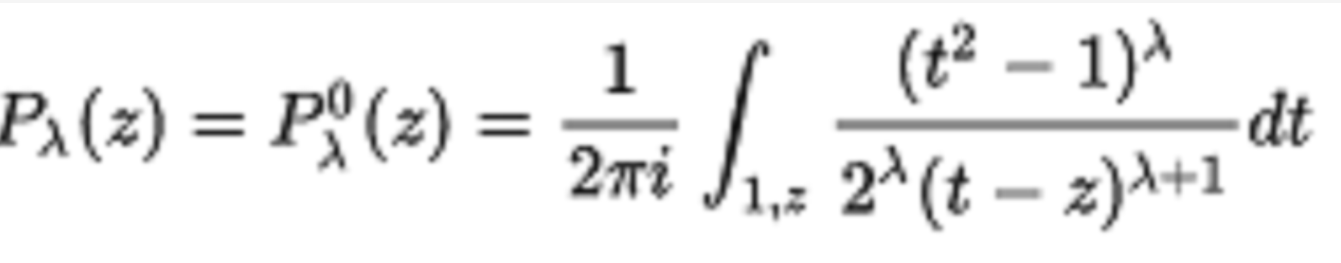
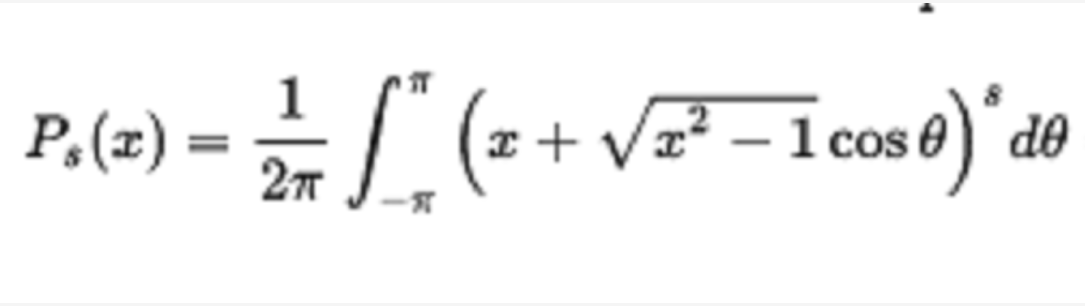
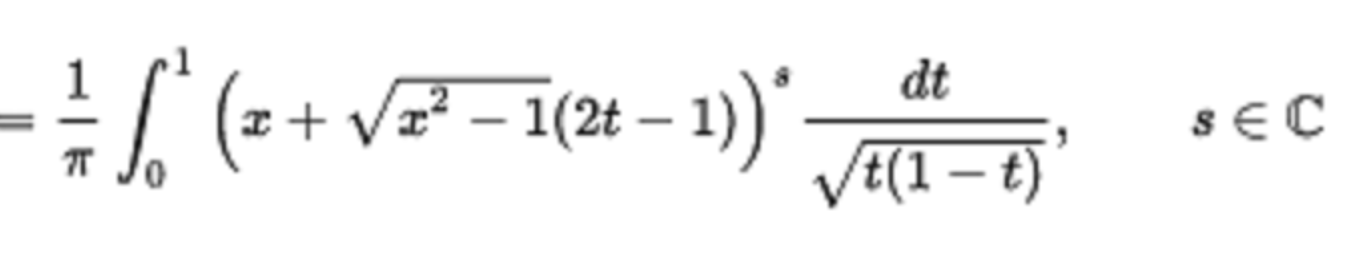
勒讓德功能為字元
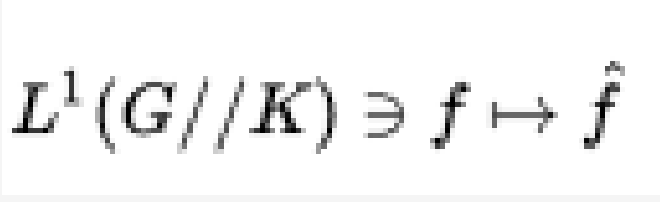
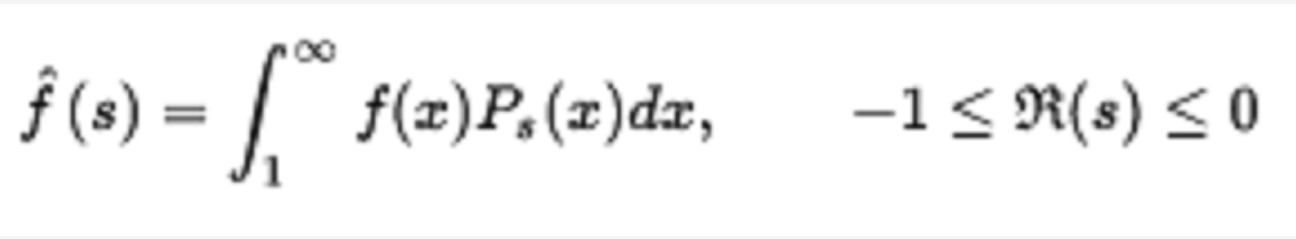
勒讓德多項式
生成函式
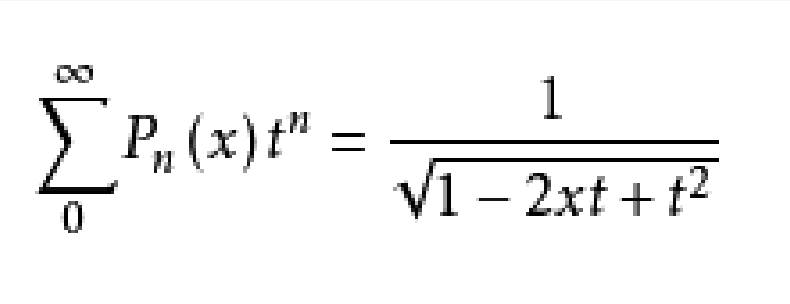
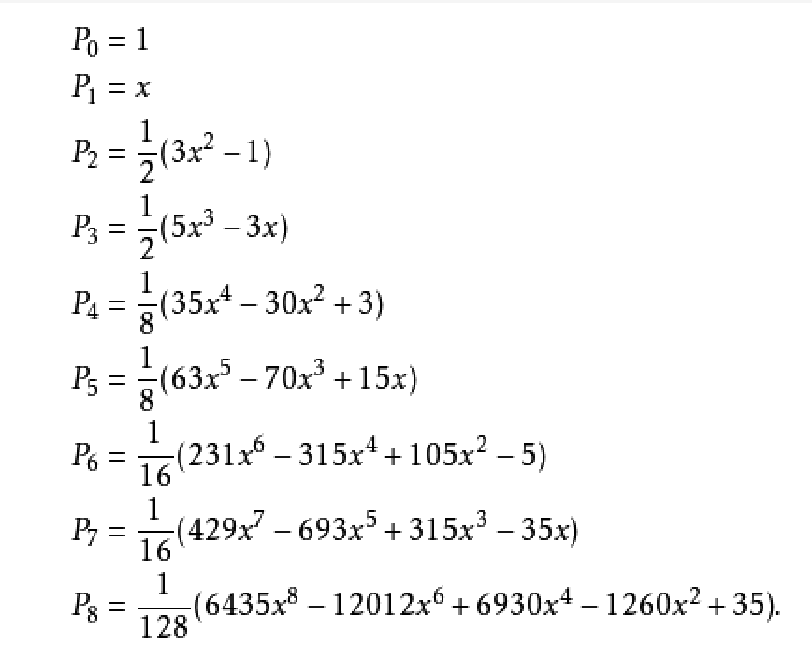
正交關係
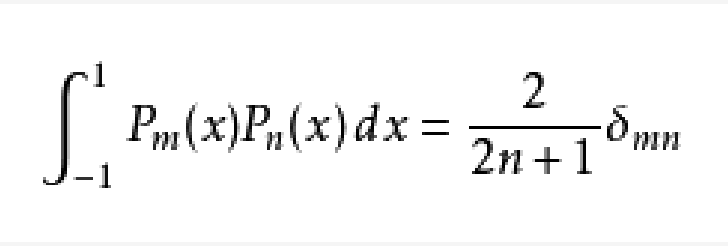
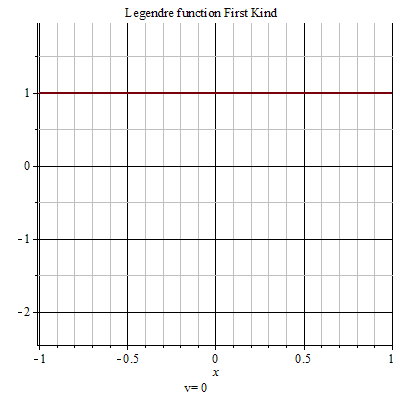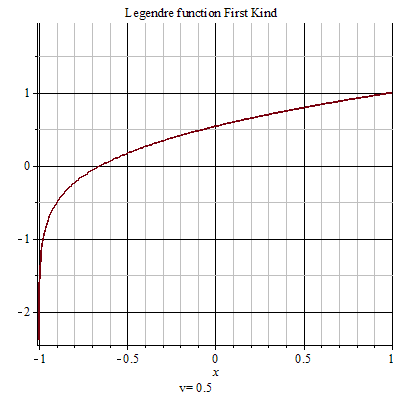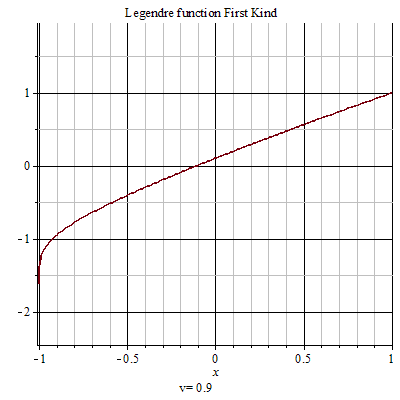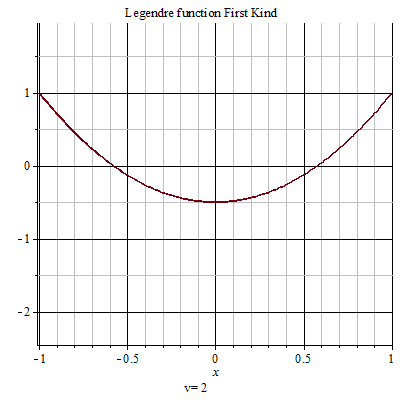
第一類勒讓德函式


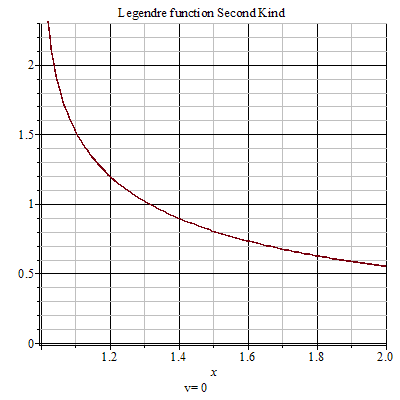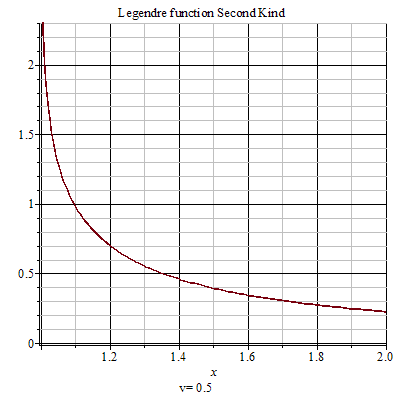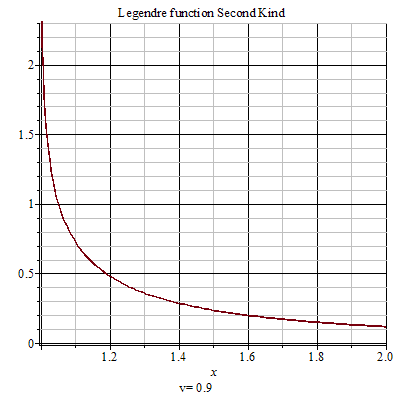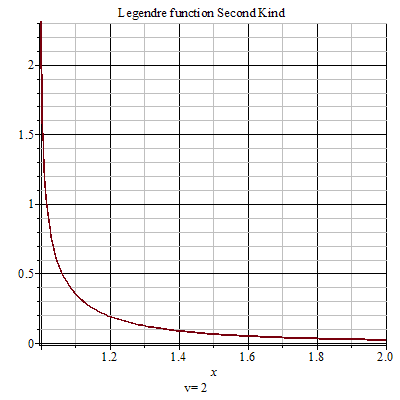
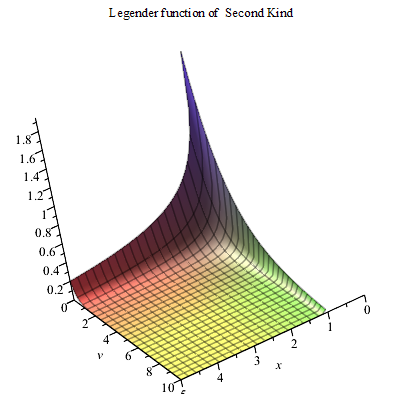
第二類勒讓德函式

在數學中,勒讓德函式Pλ,Qλ和相關的勒讓德函式Pλ,Qλ是勒讓德多項式與非整數度的泛化。
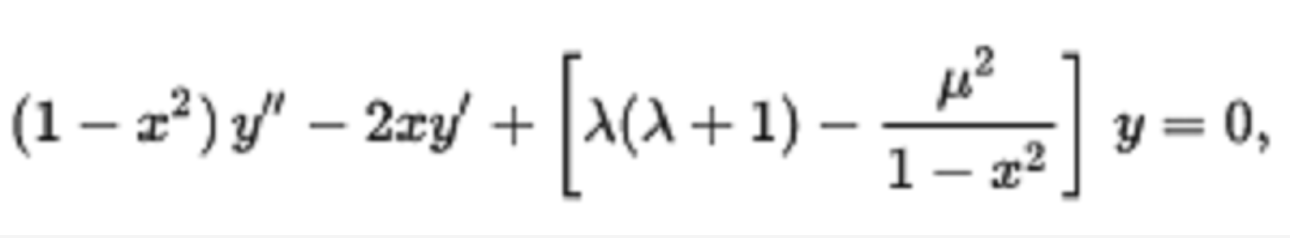

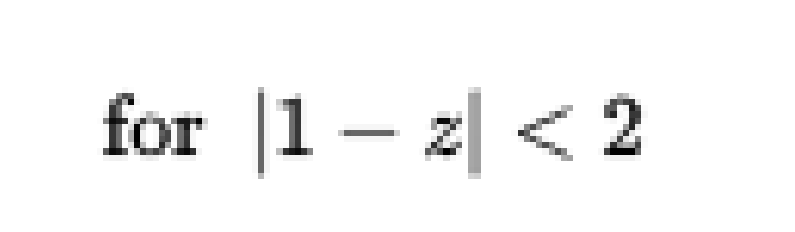
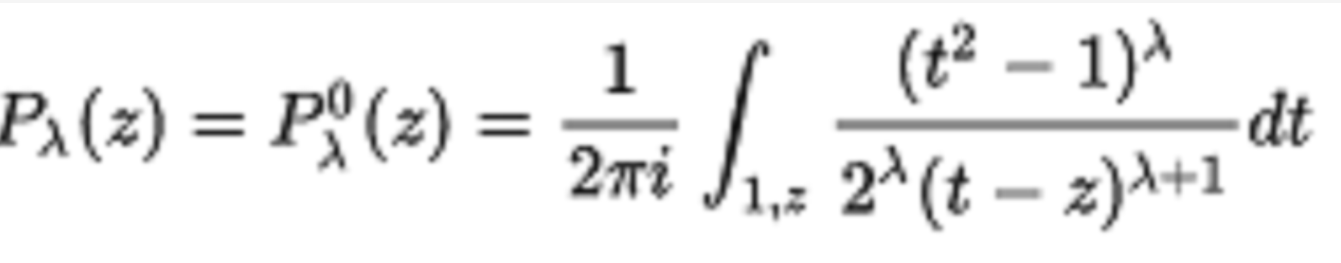
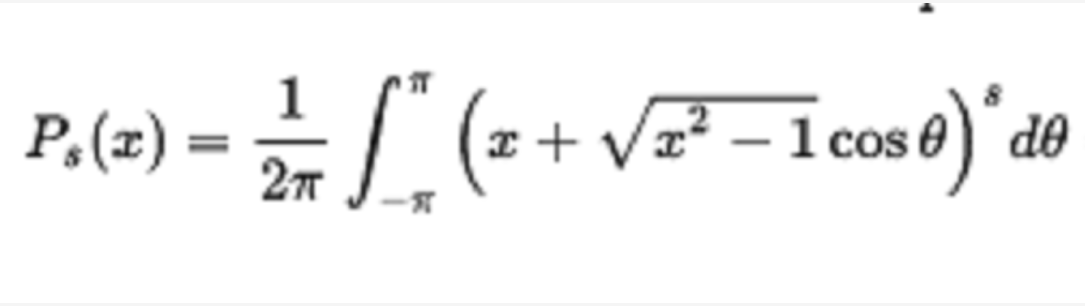
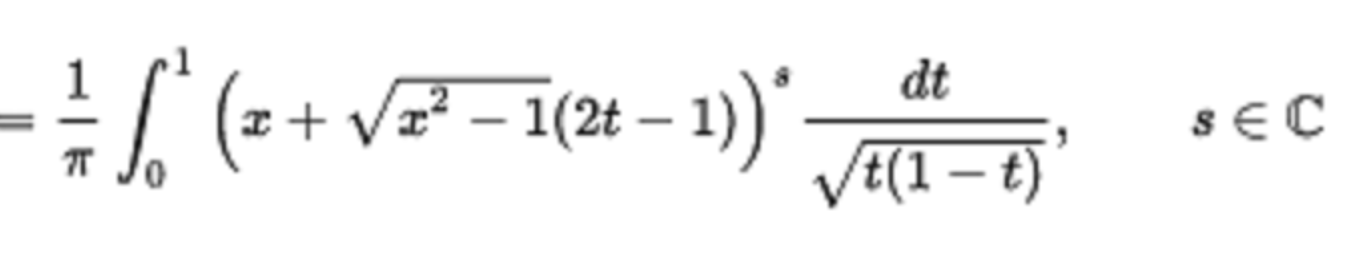
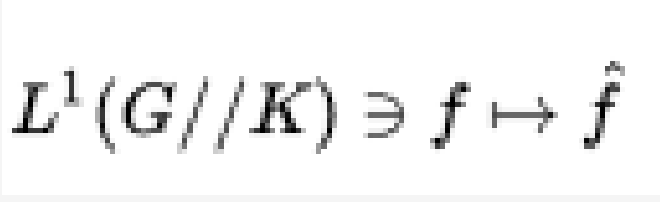
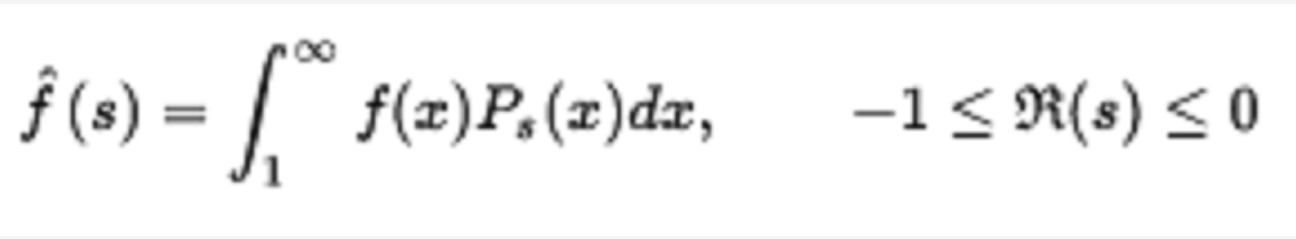
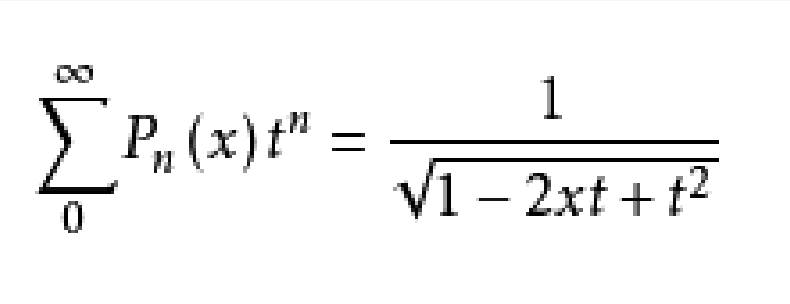
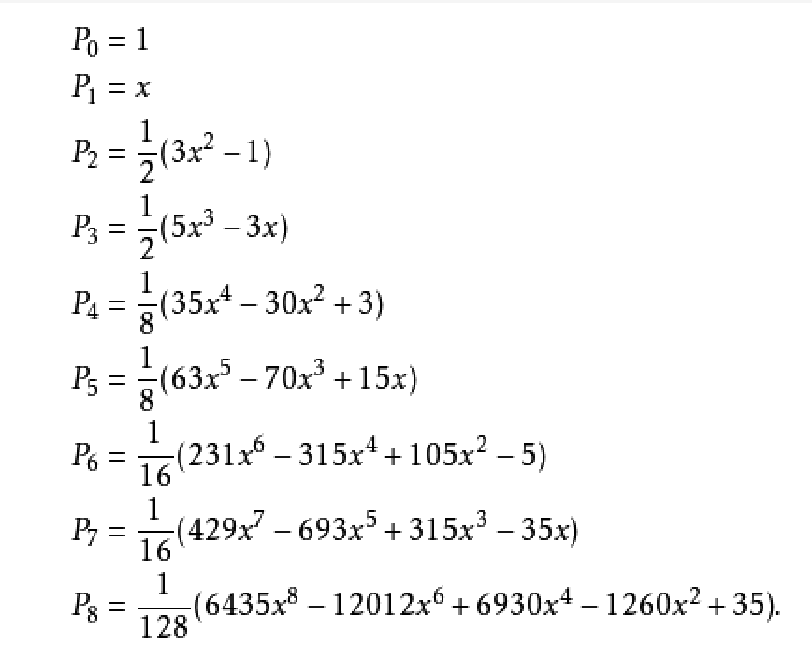
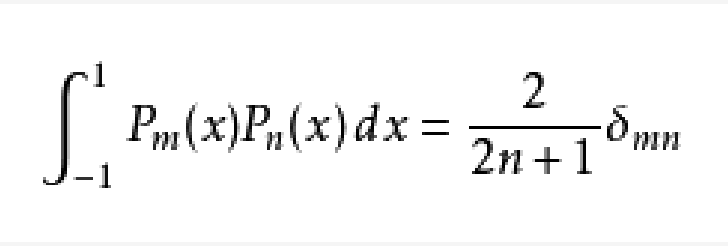






在數學中,勒讓德函式Pλ,Qλ和相關的勒讓德函式Pλμ,Qλμ是勒讓德多項式與非整數度的泛化。簡介在數學中,勒讓德函式Pλ,Qλ和相關的勒讓德函式Pλ,Qλ是勒讓德多項式與非整數度的泛化。微分方程相關的勒讓德函式是勒讓德...
勒讓德是橢圓積分理論奠基人之一。從1786年起,他就這一課題寫了大量論著,包括《積分學演習》(3卷),但證明不夠完整。《橢圓函式論》(2卷)。他已概述了這一定理及其套用,他在這方面的主要貢獻是提出三類基本的橢圓積分;證明每個橢圓積分可以表示為這三類積分的組合;編制詳盡的橢圓積分數值表。在L.歐拉提出...
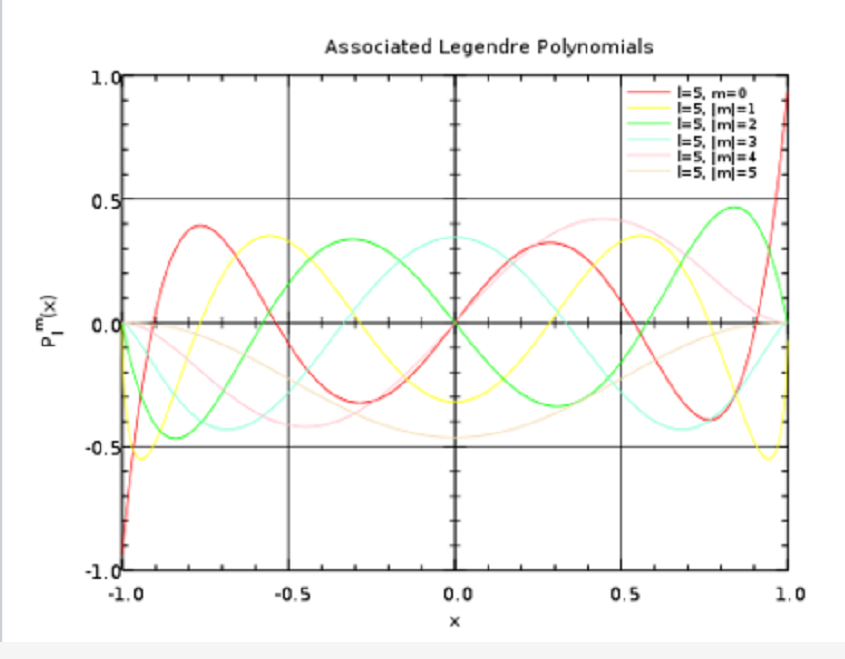
第一類連帶勒讓德函式 第二類連帶勒讓德函式 連帶勒讓德函式的母函式 由勒讓德多項式的母函式公式 兩次對x微分m次,得 .兩端同乘以 ,得 .因此, 即為連帶勒讓德函式 的母函式。連帶勒讓德函式的遞推公式 (1) .(2) .(3) .(4) .連帶勒讓德函式的正交歸一性 連帶勒讓德函式的正交歸一性是指...
球體波函式亦稱球體函式。在一定區域內,球體波函式可用連帶勒讓德函式及貝塞爾函式的級數表示。簡介 球體波函式是亥姆霍茲方程的解,通過將方程寫在球狀坐標中並套用分離變數的技術,就像使用球面坐標導致球諧函式一樣。 如果使用扁球狀坐標,則稱為扁圓球形波函式,如果使用長橢球坐標,則為橢球形波函式。如果不使用...
勒讓德符號有許多有用的性質,可以用來加速計算。它們包括: (它是一個完全積性函式。這個性質可以理解為:兩個剩餘或非剩餘的乘積是剩餘,一個剩餘與一個非剩餘的乘積是非剩餘。)如果a≡b(modp),則 這個性質稱為二次互反律的第一補充。這個性質稱為二次互反律的第二補充。一般的二次互反律為:如果p和...
圓錐函式(英文名:conical function)是在錐形區域中解某些邊值問題時出現的一類特殊函式。概念 圓錐函式(conical function)是在錐形區域中解某些邊值問題時出現的一類特殊函式。即微分方程:的解:它們是連帶勒讓德函式P(z)和Q(z)的特殊情形。連帶勒讓德函式 連帶勒讓德函式有兩類:第一類連帶勒讓德函式、第二類...
球函式(spherical function)通常指連帶勒讓德方程的解,亦即連帶勒讓德函式。有時也把面調和函式稱為球函式。在球坐標系中用分離變數法解拉普拉斯方程或亥姆霍茲方程時可出現這些函式。在現代數學中,球函式及其推廣已被廣泛套用於拓撲群的酉表示。知識要點 在函式u可能與φ角有關的一般情況下,方程▽²u=0的分離...
通常指連帶勒讓德方程的解,亦即連帶勒讓德函式。有時也把面調和函式稱為球函式。在球坐標系中用分離變數法解拉普拉斯方程或亥姆霍茲方程時可出現這些函式。在現代數學中,球函式及其推廣已被廣泛套用於拓撲群的酉表示。連帶勒讓德方程 連帶勒讓德方程(Associated Legender equation) 是一個二階常微分方程。 如果 ...
勒讓德型橢圓積分(elliptic integral in Lege-ndre's form)亦稱不完全橢圓積分.橢圓積分的一種常用的標準形式.根據被積函式的解析性質,可分為 分別稱為第一類、第二類和第三類(不完全)橢圓積分,對應於被積函式除根式型枝點外沒有奇點、或只有留數為。的極點、或具有留數不為。的極點這三種情形.k稱為...
勒讓德條件是弱極值的一個必要條件,平穩函式 使泛函 取極小值(或極大值)的必要條件是 稱其為勒讓德條件。此外,若沿著場的平穩曲線滿足條件 ,則稱為嚴格勒讓德條件。若 則稱為強勒讓德條件。對一般的 ,勒讓德條件是 對強勒讓德條件,“≥”改為“>”。相關介紹 對於一個給定的最簡泛函,...
連帶勒日德函式 微分方程 連帶勒讓德函式(Associated Legendre functions)德方程的解 連帶勒讓德函式有兩類:第一類連帶勒讓德函式、第二類連帶勒讓德函式 第一類連帶勒讓德函式 第二類連帶勒讓德函式
超球函式(hyperspherical function)是超球微分方程的兩個基本解。即函式:其中P(z)和Q(z)分別是第一類和第二類連帶勒讓德函式。顯然,μ=0時,P(z)和Q(z)就是P(z)和Q(z)。而當Pₙ(z)為正整數n時,Pₙ(z)成為多項式,即格根鮑爾多項式Cₙ(z)。超球微分方程 超球微分方程是數學物理中常見的常...
勒讓德多項式的數學描述如下:式中,下圖為幾個低階的勒讓德多項式:定義二 在區間[一1,1]帶權函式ρ(x)=1的正交多項式為 它稱為勒讓德(Legendre)多項式。由於(x²-1)ⁿ是2n次多項式,求n階導數後.得到 於是,得到首項(最高次項)xⁿ的係數 顯然.首項係數為1的勒讓德多項式為 性質 正交性 ...
圓環函式(ring function or toroidal function)是圓環坐標系下求解拉普拉斯方程時出現的一類特殊函式,即微分方程: 的解: 它們是連帶勒讓德函式P(z)和Q(z)的特殊情形。圓環坐標系(η,θ,φ)和直角坐標系之間的關係是:拉普拉斯方程 拉普拉斯方程是以法國數學家、天文學家P.S.拉普拉斯(Pierre SimonLaplace)命名...
第二類勒讓德函式 第二類勒讓德函式(Legendre function of the second kind)是1993年公布的數學名詞。公布時間 1993年,經全國科學技術名詞審定委員會審定發布。出處 《數學名詞》第一版。
勒讓德微分方程 勒讓德微分方程(Legendre differential equation)是1993年公布的數學名詞,出自《數學名詞》第一版。公布時間 1993年,經全國科學技術名詞審定委員會審定發布。出處 《數學名詞》第一版。
第一類勒讓德函式 第一類勒讓德函式(Legendre function of the first kind)是1993年公布的數學名詞。公布時間 1993年,經全國科學技術名詞審定委員會審定發布。出處 《數學名詞》第一版。
均為整數時方程的解稱為伴隨勒讓德多項式;把 和 為一般實數或複數時方程的解稱為廣義勒讓德函式(generalized Legendre functions)。當 為整數時,方程的解即為一般的勒讓德多項式。注意當 m 為奇數時,連帶勒讓德多項式並不是多項式。正交性 與勒讓德多項式一樣,伴隨勒讓德多項式在區間 [-1,1] 上也...
6特殊函式 6.1貝塞爾函式的推導 6.1.1冪級數解法 6.1.2貝塞爾函式 習題6.1 6.2貝塞爾函式的性質 6.2.1貝塞爾函式的遞推公式 6.2.2貝塞爾函式的零點與正交模 6.2.3函式按貝塞爾函式系展開 習題6.2 6.3貝塞爾函式的套用 習題6.3 6.4勒讓德函式 6.4.1勒讓德方程的求解 6.4.2勒讓德多項式 習題...
4.2 勒讓德多項式 4.2.1 勒讓德多項式 4.2.2 勒讓德多項式的微分和積分表示 4.3 勒讓德多項式的性質 4.3.1 勒讓德函式的母函式 4.3.2 勒讓德多項式的遞推公式 4.3.3 勒讓德多項式的正交歸一性 4.3.4 廣義傅立葉級數展開 4.4 勒讓德多項式在解數理方程中的套用 4.5 連帶勒讓德函式 4....
3.1.3 脈衝函式δ(t)3.1.4 單位階躍函式h(t)3.1.5 δ(c)和h(t)的matlab算法 3.2 常微分方程在常點鄰域內的級數解 3.2.1 常微分方程的常點、奇點和正則奇點 3.2.2 埃爾米特方程的冪級數解 3.2.3 計算機軟體maple的調用 3.2.4 用計算機軟體求算埃爾米特多項式 3.3 勒讓德函式 3.3.1 ...
