雙軸球面函式

雙軸球面函式(biaxial spherical surface function)是在坐標系中改變極軸方向時出現的球函式。

基本介紹

• 中文名：雙軸球面函式
• 外文名：biaxial spherical surface function
• 領域：數學
• 學科：函式
• 性質：球函式
• 定義：在坐標系中改變極軸方向

概念

雙軸球面函式(biaxial spherical surface function)是在坐標系中改變極軸方向時出現的球函式。設空間兩點的直角坐標為(x，y，z)和(x′，y′，z′)，相應的球坐標為(r，θ，φ，)和(r′，θ′，φ′).(θ，φ)方向與(θ′，φ′)方向的夾角為γ(如圖1)，

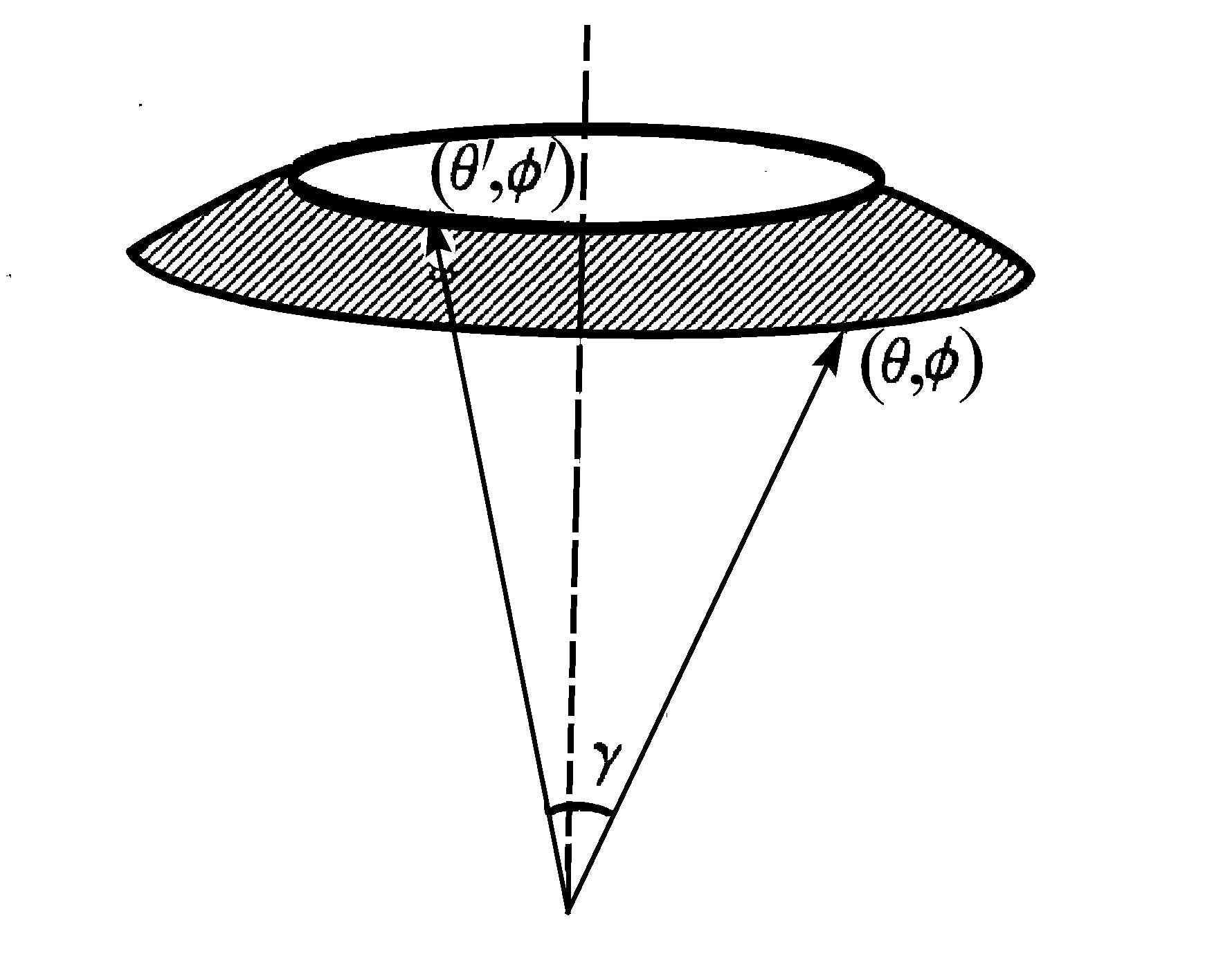
圖1 (θ，φ)，(θ′，φ′)方向及其夾角γ

則：

為雙軸球面函式，即以(θ′，φ′)方向為極軸時(θ，φ)方向的球面函式。它可以用兩各別方向的球面函式表示：

這個公式又稱為勒讓德多項式的加法定理。

球函式

通常指連帶勒讓德方程的解，亦即連帶勒讓德函式。有時也把面調和函式稱為球函式。在球坐標系中用分離變數法解拉普拉斯方程或亥姆霍茲方程時可出現這些函式。

在現代數學中，球函式及其推廣已被廣泛套用於拓撲群的酉表示。

連帶勒讓德方程

連帶勒讓德方程（Associated Legender equation） 是一個二階常微分方程。

如果 ，連帶勒讓德方程化為勒讓德方程：

連帶勒讓德方程的解為：

微分方程

微分方程指含有未知函式及其導數的關係式。解微分方程就是找出未知函式。

微分方程是伴隨著微積分學一起發展起來的。微積分學的奠基人Newton和Leibniz的著作中都處理過與微分方程有關的問題。微分方程的套用十分廣泛，可以解決許多與導數有關的問題。物理中許多涉及變力的運動學、動力學問題，如空氣的阻力為速度函式的落體運動等問題，很多可以用微分方程求解。此外，微分方程在化學、工程學、經濟學和人口統計等領域都有套用。

數學領域對微分方程的研究著重在幾個不同的面向，但大多數都是關心微分方程的解。只有少數簡單的微分方程可以求得解析解。不過即使沒有找到其解析解，仍然可以確認其解的部分性質。在無法求得解析解時，可以利用數值分析的方式，利用電腦來找到其數值解。動力系統理論強調對於微分方程系統的量化分析，而許多數值方法可以計算微分方程的數值解，且有一定的準確度。

含有未知函式的導數，如的方程是微分方程。 一般的凡是表示未知函式、未知函式的導數與自變數之間的關係的方程，叫做微分方程。未知函式是一元函式的，叫常微分方程；未知函式是多元函式的叫做偏微分方程。微分方程有時也簡稱方程。

球坐標系

球坐標系是三維坐標系的一種，用以確定三維空間中點、線、面以及體的位置，它以坐標原點為參考點，由方位角、仰角和距離構成。球坐標系在地理學、天文學中都有著廣泛套用。

在學術界內，關於球坐標系的標記有好幾個不同的約定。按照國際標準化組織建立的約定（ISO 31-11），徑向距離、天頂角、方位角，分別標記為。這種標記在世界各地有許多使用者。通常，物理界的學者也採用這種標記。而在數學界，天頂角與方位角的標記正好相反：被用來代表天頂角，被用來代表方位角。數學界的球坐標標記是。這種標記的優點是較廣的相容性；在二維極坐標系與三維圓柱坐標系里，都同樣地代表徑向距離，也都同樣地代表方位角。本條目採用的是物理標記約定。

在數學裡，球坐標系（英語：Spherical coordinate system）是一種利用球坐標表示一個點 p 在三維空間的位置的三維正交坐標系。圖2顯示了球坐標的幾何意義：原點與點 P 之間的徑向距離 r ，原點到點 P 的連線與正 z-軸之間的天頂角以及原點到點 P 的連線，在 xy-平面的投影線，與正 x-軸之間的方位角。

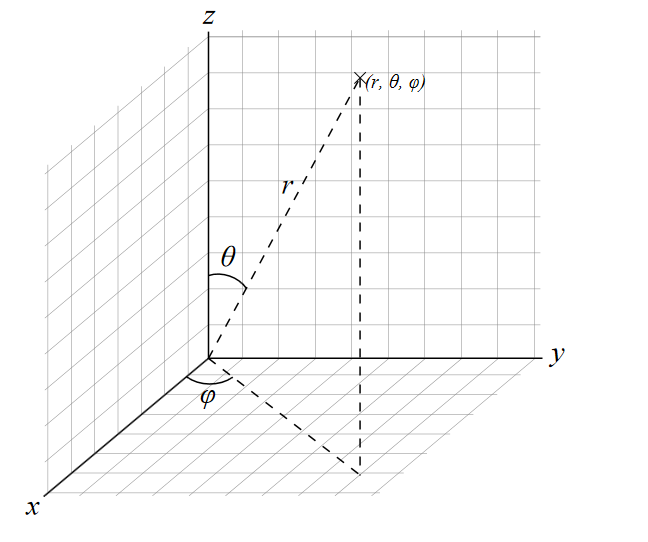
圖2 平面坐標系