基本介紹
- 中文名:伴隨勒讓德多項式
- 外文名:Associated Legendre polynomials
- 分類:數學物理、微分方程
- 領域:數理科學
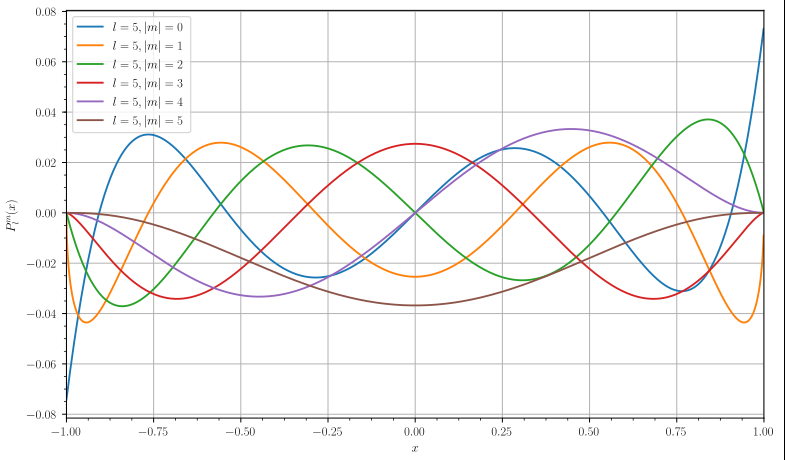
定義









正交性


與勒讓德多項式的關係

與超幾何函式的關係

負數階連帶勒讓德多項式


與球諧函式的關係




















伴隨勒讓德多項式(Associated Legendre polynomials,又譯締合勒讓德多項式、連帶勒讓德多項式、關聯勒讓德多項式)是數學上對常微分方程解函式序列的稱呼,在數學和理論物理學中有重要的意義。定義數學...
它稱為勒讓德(Legendre)多項式。由於(x²-1)ⁿ是2n次多項式,求n階導數後.得到 於是,得到首項(最高次項)xⁿ的係數 顯然.首項係數為1的勒讓德多項式為 性質 正交性 2.奇偶性 Pₙ(-x)=(-1)ⁿPₙ(x)事實上,(x²—1)ⁿ是偶函式,經過偶數次求導仍為偶函式,經過奇數次求導仍為奇...
大Q勒讓德多項式 大Q勒讓德多項式,術語。'''大q-勒讓德多項式'''是一個以[[基本超幾何函式]]定義的正交多項式Roelofp443::==正交性==
連帶勒讓德函式是連帶勒讓德方程 的解,當 為任意整數的情形時,連帶勒讓德方程為 的一個解 記作 .另一個解為 記作 ,即 .( ) , 分別稱為m階n次第一類連帶勒讓德和第二類連帶勒讓德函式。第一類連帶勒讓德函式 第二類連帶勒讓德函式 連帶勒讓德函式的母函式 由勒讓德多項式的母函式公式...
是伴隨勒讓德多項式,用方程式定義為 而 是 l階勒讓德多項式,可用羅德里格公式表示為 徑向部分解答 徑向函式滿足一維薛丁格方程式:方程式左邊的第二項可以視為離心力位勢,其效應是將徑向距離拉遠一點。除了量子數 ℓ 與 m以外,還有一個主量子數 n。為了滿足 R(r) 的邊界條件,n必須是正值整數,能量也離...
這個公式又稱為勒讓德多項式的加法定理。球函式 通常指連帶勒讓德方程的解,亦即連帶勒讓德函式。有時也把面調和函式稱為球函式。在球坐標系中用分離變數法解拉普拉斯方程或亥姆霍茲方程時可出現這些函式。在現代數學中,球函式及其推廣已被廣泛套用於拓撲群的酉表示。連帶勒讓德方程 連帶勒讓德方程(Associated Lege...
,這兩個微分方程可以簡化成滿足伴隨勒讓德多項式的式子。當給定 ,角波函式可被展開成勒讓德級數。注意,如果我們將角波函式寫成 ,函式 將滿足以下線性微分方程:此函式為球波函式。發展 現存不少不同的球函式標準化的方法,在Abramowitz and Stegun。的文章中有整理的表格。Abramowitz跟Stegun(以及現在的相關文章)...
2.8 勒讓德多項式 69 2.8.1 從冪函式1,x,x2,...的正變化作出勒讓德多項式 69 2.8.2 母函式 71 2.8.3 勒讓德多項式的其他性質 72 2.9 其他正交組的例子 73 2.9.1 導致勒讓德多項式的問題的推廣 73 2.9.2 切比雪夫多項式 74 2.9.3 雅可比多項式 76 2.9.4 埃爾米特多項式 77 2.9....
伴隨(締合)勒讓德多項式;為地球引力位的位係數。地球自轉的影響 地球自轉是地球的一種重要運動形式,由於受到外部天體(主要是月球和太陽)的影響,同時由於地球本身(包括大氣、海洋和固體地球)各種複雜的物態和運動形式的影響,地球自轉呈現出極其複雜的規律。對地球自轉規律的研究一直是天文學和地球科學相互交叉滲透...
球諧函式表是一個數理科學術語。定義 這裡列出球諧函式,以方程式表示為 其中, 為正值整數, 為小於或等於 的正值整數, 是伴隨勒讓德多項式,以方程式表示為 表內有些方程式也給出直角坐標版本。球坐標與直角坐標之間的變換關係是 函式表 l=0 l=1 l=2 l=3 l=4 l=5 l=6 l=7 l=8 l=9 l=10 ...
是伴隨勒讓德多項式,用方程定義為 而 是 階勒讓德多項式,可用羅德里格公式表示為 徑向部分解答 將角部分解答代入薛丁格方程,則可得到一個一維的二階微分方程:設定函式 。代入方程(1)。經過一番繁雜的運算,可以得到 徑向方程變為 其中,有效位勢 。這正是函式為 ,有效位勢為 的薛丁格方程。徑向距離r的...
