基本介紹
- 中文名:分母有理化
- 外文名:Rationalize the denominator
- 作用:分母有理化,會使根式的運算簡便
- 方法:分解約簡法
- 適用人群:國中、高中階段
- 學科:數理科學
定義
單項式
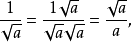
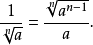
二項式
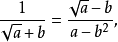
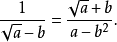
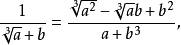
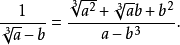
多項式
逐項有理化
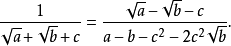
輾轉相除法
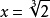
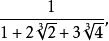
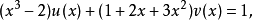
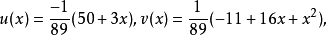
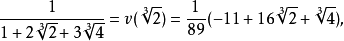
待定係數法
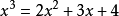
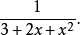
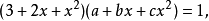
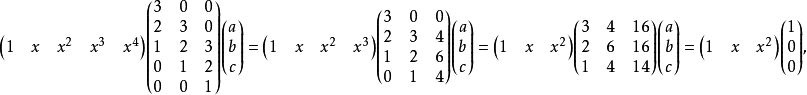
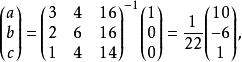
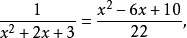
常規方法
分母是一個單項式
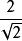
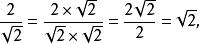
分母是一個多項式
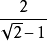
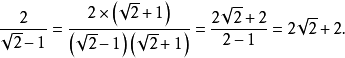
特殊方法
分解約簡法
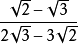
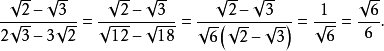
配方約簡法
注意事項

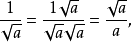
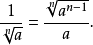
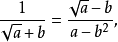
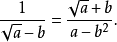
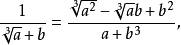
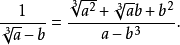
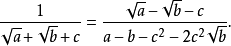
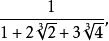
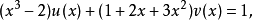
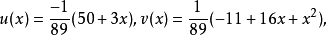
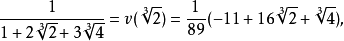
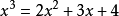
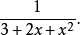
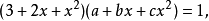
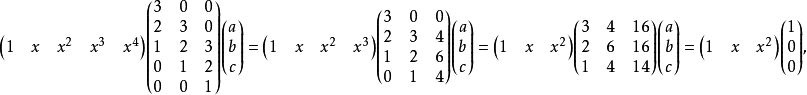
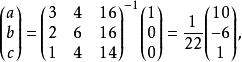
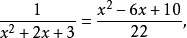
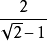
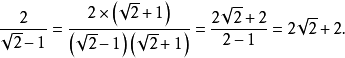
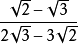
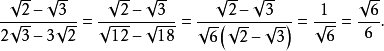
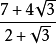
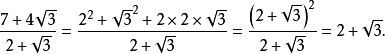
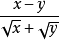
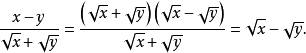
分母有理化(fēn mǔ yǒu lǐ huà)(Rationalize the denominator),又稱"有理化分母",指的是在二次根式中分母原為無理數,而將該分母化為有理數的過程,也...
分母有理化(fēn mǔ yǒu lǐ huà)(Rationalize the denominator),又稱"有理化分母",指的是在二次根式中分母原為無理數,而將該分母化為有理數的過程,也...
常用有理化因式有:與 , 與 , 與 , 與 , 與 。 [1] 二次根式分母有理化 在分母含有根號的式子中,把分母的根號化去,叫做分母有理化。...
10.根式運算法則:⑴加法法則(合併同類二次根式);⑵乘、除法法則;⑶分母有理化:A. ;B. ;C. .三、 套用舉例(略)四、 數式綜合運算(略)...
又稱“有理化分母”,是指通過適當的變形划去代數式分母中根號的運算。一般情況下,在進行根式運算及把一個根式化成最簡根式時,都要將分母有理化,兩個含有根式的...
第一步是使分數的分母有理化。[1] 參考資料 1. rationalize是什麼意思 .海詞詞典[引用日期2016-08-6] 詞條標籤: 文化 V百科往期回顧 詞條統計 瀏覽次數:次...
122 1992年第11期 《學生之友》 分母有理化的若干技巧123 1992年第11期 《高中生語數外》(月刊) 巧求定點坐標124 1992年第11期 《中學生數理化》 判別式...
分析:為了使分母有理化,嘗試將分子化為含有因式(1+√2-√3)的多項式。注意到√6=√2·√3,即可設3+2√2-√3-√6=(1+√2-√3)(a√2+b√3+c),...
(a+√b)+(a-√b)=2a, (a+√b)(a-√b)=a^2-b.共軛根式可以用來分母有理化,(c+√d)/(a+√b)=(c+√d)(a-√b)/(a+√b)(a-√b)=(ac+...
1 定義 2 常用的共軛根式 3 套用 ▪ 有理化分母 ▪ 有理化分子 共軛根式定義 編輯 所謂共軛根式,是指兩個不等於零的根式A、B,若它們的積AB不含根...
②利用共軛複數將分母實數化得(見右圖):點評:①是常規方法;②是利用國中我們學習的化簡無理分式時,都是採用的分母有理化思想方法,而複數c+di與複數c-di,相當於...
(2)分母有理化(368―377) (3)根式的加減法(378-382) (4)根式的乘除法(383-386) (5)根式的乘方與開方(387―397) (6)根式的化簡與求值(398―418) (7...
07 5、把分母有理化的題目分類(例題3道)B028 初二 幾何 ①01 一、三角形的直線與線段02 二、三角形內角和定理的證明03 三、性質、判定和定義...
38.三項式的分母有理化 39.分式型根式的化簡 四 方程與方程組 40.解二元一次方程組五法 41.解三元一次方程組三法 42.輪換方程組的解法 43.二元一次方程組中...
16.3(3) 二次根式的分母有理化 16.3(4) 二次根式的混合運算 階段訓練2 本章複習題 第17章 一元二次方程 17.1 一元二次方程的概念 17.2(1) 特殊的...
進而得出方程的解。如果分母上有無理數,則需要先將分母有理化。一元一次方程求根公式法 基本公式對於關於 的一元一次方程 ,其求根公式為:推導過程解:移項,得:...
(2)當一個式子的分母中含有二次根式時,一般應把它化簡成分母中不含二次根式的式子,也就是把它 的分母有理化. 最簡二次根式 根據最新人教版教材、浙教版等教...
結尾相同:事化 表面化 分母有理化 窮神觀化 造化 千變萬化 修短隨化 比較文化 規範化 默化 簡化 委化 翊化 同化 執而不化 馬家浜文化 公式化 淨化。 [1]...
第五節 二次根式的分母有理化 第六節 實數的整數部分和小數部分 第四章 三角形 第一節 求線段長或證明線段相等 第二節 求角的大小或證明角相等 第三節 證明...
分母有理化、最簡二次根式、同類二次根式、二次根式的加減法、二次根式的混合運算、有理化因式、二次根式的化簡、分數指數冪 12.代數方程 12.1 一元二次方程 ...
