設y1=x1+x2,y2=x1^2+x2^2,y3=x1*x2,這三個函式之間有下述關係:y1^2-y2-2y3=0。像這樣三個函式被稱為函式相關的。但若只考慮y1、y2,那就不可能找到y1和y2之間的一個恆等式,於是這兩個函式之間被稱為函式無關的。
基本介紹
- 中文名:函式的相關性
- 外文名:dependence of functions
- 相關:函式相關定理是隱函式定理的最好運用
- 分類:數學
- 套用學科:數學分析
- 相關名詞:函式
定義















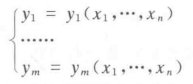 圖1
圖1
判斷定理
















 圖2
圖2 圖3
圖3 圖4
圖4特殊情況


 圖5
圖5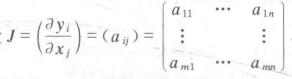 圖6
圖6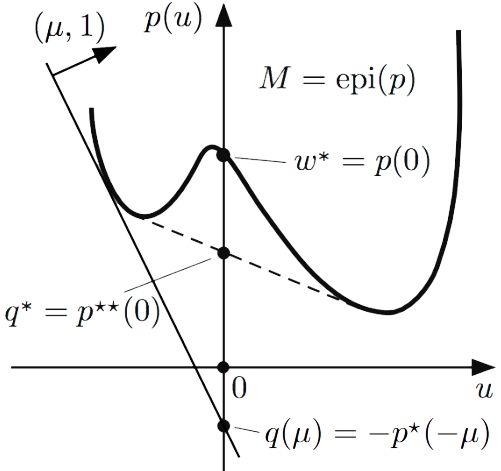
設y1=x1+x2,y2=x1^2+x2^2,y3=x1*x2,這三個函式之間有下述關係:y1^2-y2-2y3=0。像這樣三個函式被稱為函式相關的。但若只考慮y1、y2,那就不可能找到y1和y2之間的一個恆等式,於是這兩個函式之間被稱為函式無關的。















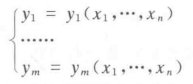 圖1
圖1
















 圖2
圖2 圖3
圖3 圖4
圖4

 圖5
圖5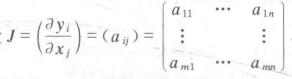 圖6
圖6中處處函式相關。(3)=>(1),明顯成立。套用 數據依賴,是指一個關係內部屬性與屬性之間的一種約束關係。數據依賴主要包括函式依賴(Functional Dependency,簡記為FD)和多值依賴,而函式依賴也就是函式的相關性,它描述了一個關係框...
相關函式是描述信號X(s),Y(t)(這兩個信號可以是隨機的,也可以是確定的)在任意兩個不同時刻s、t的取值之間的相關程度。...
,就稱這個二元關係是從集合A到集合B的一個函式或者映射。記作 或者 也可改寫為 ,其中y稱為x的象,而x則稱為y的原象。稱集合A是函式的定義域,集合A中所有元素在函式 的作用下得到的所有象的集合稱為函式 的象或函式...
復相關係數:又叫多重相關係數。復相關是指因變數與多個自變數之間的相關關係。例如,某種商品的季節性需求量與其價格水平、職工收入水平等現象之間呈現復相關關係。典型相關係數:是先對原來各組變數進行主成分分析,得到新的線性關係的...
非線性回歸分析必須著重解決以下兩個問題:第一,如何確定非線性函式的具體形式。與線性回歸分析的場合不同,非線性回歸函式有多種多樣的具體形式,需要根據所要研究的問題的性質並結合實際的樣本觀測值做出恰當的選擇。第二。如何估計函式中...
特別是對於實函式f(x)和h(x)而言,其相關運算相當於求兩函式的曲線相對平移 1個參變數x後形成的重疊部分與橫軸所圍區域的面積。定義 兩個函式f(x)和h(x)的互相關,由含參變數x的無窮積分定義,即 或 類似於卷積,這裡,參變數...
在統計學中,皮爾遜相關係數( Pearson correlation coefficient),又稱皮爾遜積矩相關係數(Pearson product-moment correlation coefficient,簡稱 PPMCC或PCCs),是用於度量兩個變數X和Y之間的相關(線性相關),其值介於-1與1之間。函式...
正比,有一個確定的比例係數,如正比例函式:y=2x,比例係數是2,那么,可見,這樣,每當x增加1時,相應的y值就會增加2。這樣,每當x減少1時,相應的y值就會減少2。更準確地說,每當x增加1時,相應的y值就會增加1的2倍。這樣,...
例如,在消費函式中,t期的消費不僅取決於t期的收人,還取決於前一期的收入水平,如果查明自相關性是由於略去的前一期收入水平 引起的,則只要將前一期收入 作為解釋變數加入模型,模型中的自相關就會消除。即 其中, 表示t期的...
例如,在時序n=a~b的數位訊號x(n)與另一個數位訊號y(n)逐段比較,其相關函式寫為 式中a和b都是整數,符號“*”表示複數共軛。相關函式的絕對值|r(n)|沒有最大值,但它可通過數字之間的相對大小提供隱藏在被比較信號中的信息...
互相關函式是信號分析里的概念,表示的是兩個時間序列之間的相關程度,即描述信號x(t),y(t)在任意兩個不同時刻t1,t2的取值之間的相關程度。描述兩個不同的信號之間的相關性時,這兩個信號可以是隨機信號,也可以是確知信號。互...
多項式相關性 多項式相關性(polynomial relatedness)複雜性測度間的一種特殊相關性.它是兩種複雜測度在多項式意義下的等價性.設}_ {}; };E},,'1}'= {tl}'; };E},為兩個複雜性測度.對任何一元函式t,令Pol ...
正比,有一個確定的比例係數,如正比例函式:y=2x,比例係數是2,那么,可見,這樣,每當x增加1時,相應的y值就會增加2。這樣,每當x減少1時,相應的y值就會減少2。更準確地說,每當x增加1時,相應的y值就會增加1的2倍。這樣,...
對稱性:從定義顯然可以看出R(i) = R(−i)。連續型自相關函式為偶函式。當f為實函式時,有:當f是複函數時,該自相關函式是厄米函式,滿足:其中星號表示共軛。連續型實自相關函式的峰值在原點取得,即對於任何延時 τ,均有 |...
相關係數函式 corrcoef 格式 corrcoef(X,Y) %返回列向量X,Y的相關係數,等同於corrcoef([X Y]).corrcoef (A) %返回矩陣A的列向量的相關係數矩陣 >> A=[1 2 3;4 0 -1;1 3 9]A = 1 2 3 4 0 -1 1 3 9 >> C1=...
在時間序列分析分析中[1],對於時間序列{X,x∈T},任取t,s∈T,定義γ(t,s)為序列{X}的自協方差函式:γ(t,s)=E(X-μ)(X-μ)定義ρ(t,s)為時間序列{X}的自相關係數,簡記為ACF:ρ(t,s)= γ(t,s)/sqrt(DX...
因自相關函式中每一個回歸係數Φ恰好表示x與x在排除了其中間變數x,x,...,x影響後的自相關係數,即x-Φx-Φx-...-Φx=Φx+u中的Φ,所以偏自相關函式由此得名。偏自相關函式的定義 用Φx+Φx+...+Φx+u,表示k階...
相關分析法建模,通過對系統輸入和輸出的相關函式之間的關係進行分析建立系統的數學模型。介紹 通過對系統輸入和輸出的相關函式之間的關係進行分析建立系統的數學模型。這種方法可以比較有效地克服系統輸出中含有的隨機噪聲給建模帶來的困難。適...
以澳大利亞的兩個相鄰風電場實測出力為例,在含多風電場的 IEEE30節點系統中對所提方法進行驗證,算例結果表明採用所提方法確定的最優場景機率模型能準確描述多風電場輸出功率之間的相關性。Copula函式 Copula函式能夠將多維隨機變數的聯合...
在工業生產和科學研究中,經常遇到兩個之間的關係問題: 一種是兩個量之間是完全確定的函式關係;另一 種是兩個量之間是不完全確定的對應關係。對於這種既相關又不完全確定的關係,就稱為相關關係。人們套用畫相關圖,求出相關係數的...
在數學最最佳化中,Rosenbrock函式是一個用來測試最最佳化算法性能的非凸函式,由Howard Harry Rosenbrock在1960年提出 [1] 。也稱為Rosenbrock山谷或Rosenbrock香蕉函式,也簡稱為香蕉函式。Rosenbrock函式的定義如下:...
例如,δ函式δ(x,y)僅當x=y時其值為1,其他情形均為0;ζ函式ζ(x,y)僅當x≤y時其值為1,而其他情形均為0。接合代數 若A(p)為如前所述所有接合函式組成的集合,並在其上定義接合函式的加法運算、數乘運算以及卷積...
為其值域(值域是Y的子集),x叫做自變數,y叫做因變數,習慣上也說y是x的函式。對應法則和定義域是函式的兩個要素。函式相關概念 自變數,函式一個與他量有關聯的變數,這一量中的任何一值都能在他量中找到對應的固定值。因變數(...
的函式,而函式值是離散的。這個函式即為取整函式。為了方便,用 表示不超過 的最大整數,所以函式 又可記為 一般的,有 函式圖形見右。相關概念 【階梯曲線】即取整函式的在定義域 ,值域 的圖形,在為整數值處,圖形發生跳躍,...
隨著計算機套用的發展,目前頭相關傳輸函式的測量過程完全可以採用軟體控制。測量中,揚聲器產生測量信號,而位於雙耳處的傳聲器撿拾雙耳聲壓信號。雖然可直接按式(1)計算頻域的HRTF,但由於需要測量2次聲壓並涉及頻域相除,所以比較繁瑣。目前...
對勾函式是一種類似於反比例函式的一般雙曲函式,是形如f(x)=ax+b/x(ab>0)的函式。由圖像得名,又被稱為“雙勾函式”、“勾函式”、"對號函式"、“雙飛燕函式”等。常見a=b=1。函式定義 對勾函式是指形如 (ab>0)的...
