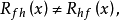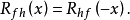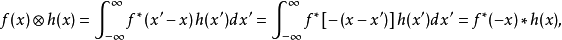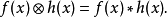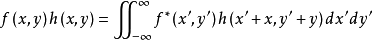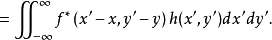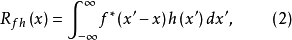兩個函式互相關的含義是:對兩個函式分別作複數共軛和反向平移並使其相乘的無窮積分,或者說:第一個函式依次作復共軛和平移後與第二個函式相乘的無窮積分。可以證明,兩個定義完全等價(可以互相導出)。從物理上看,互相關運算的結果反映了兩個信號之間相似性的量度。特別是對於實函式f(x)和h(x)而言,其相關運算相當於求兩函式的曲線相對平移 1個參變數x後形成的重疊部分與橫軸所圍區域的面積。
基本介紹
- 中文名:互相關
- 外文名:Cross correlation
- 所屬學科:數學、物理等
- 相關概念:相關、卷積、傅立葉變換等
定義
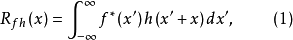
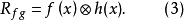
互相關的性質