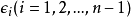基本介紹
- 中文名:Rosenbrock函式
- 提出者:Howard Harry Rosenbrock
- 提出時間:1960年
- 別稱:Rosenbrock香蕉函式
介紹,多變數下的擴展,隨機函式,可適用的最最佳化算法,相關條目,
介紹
在數學最最佳化中,Rosenbrock函式是一個用來測試最最佳化算法性能的非凸函式,由Howard Harry Rosenbrock在1960年提出。也稱為Rosenbrock山谷或Rosenbrock香蕉函式,也簡稱為香蕉函式。
Rosenbrock函式的定義如下:
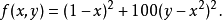
多變數下的擴展
多變數的Rosenbrock函式有以下二種形式。一種是N/2個獨立二維Rosenbrock函式的和:

另一個較複雜的形式為:
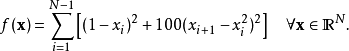

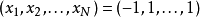

隨機函式
有許多方式可以將Rosenbrock函式延伸到隨機(stochastic)函式,以下是一種例子:

可適用的最最佳化算法
經若經過適當的坐標系調整,可以在沒有梯度信息及不創建局部近似模型的情形下(和其他不使用梯度信息的最最佳化算法相反),用最最佳化算法求得Rosenbrock函式的最小值。
相關條目
- Himmelblau函式
- Rastrigin函式