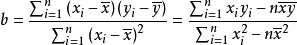正相關

正相關是指自變數增長，因變數也跟著增長。兩個變數變動方向相同，一個變數由大到小或由小到大變化時，另一個變數亦由大到小或由小到大變化。

基本介紹

• 中文名：正相關
• 外文名：Positive correlation
• 解釋：自變數增長，因變數也跟著增長
• 對稱：負相關
• 適用範圍：數理科學

定義

正相關（Positive correlation），是指兩個變數變動方向相同，一個變數由大到小或由小到大變化時，另一個變數亦由大到小或由小到大變化。即其數據曲線的切線斜率始終大於零。如身高與體重，身高越長，體重就越重。也就是說，在正相關的情況下，一個變數隨著另一個變數的變化而發生相同方向的變化（兩個變數同時變大或變小）。其中，引起變化的量叫做自變數（即自己發生變化的量），另一個變數叫做因變數（即跟著自變數變化的量）。

統計學中常用相關係數r來表示兩變數之間的相關關係。r的值介於-1與1之間,r為正時是正相關，反映當x增加(減少)時,y隨之相應增加(減少)；呈正相關的兩個變數之間的相關係數一定為正值，這個正值越大說明正相關的程度越高。

當這個正值為1時就是完全正相關的情形，如點子排為一條直線，為完全正相關。正相關雖然意思明確，其實是個模糊的概念，不可以量化，只是定性說法。如果有明確的關係，例如y=2x，這叫y與x成正比，如果只是大體上，x、y的變化方向一樣，例如x上升，y也上升或者x下降，y也下降，那么，這叫正相關。反之，x上升，y卻下降，或者x下降，y卻上升，就叫負相關了。

辨析

正比

正比是指自變數每發生一個單位的變化，因變數也會發生固定單位的同向變化。如：1.人體內的脂肪含量與年齡之間的關係。在一定年齡段內，隨著年齡的增長，人體內的脂肪含量會增加，但人體內的脂肪含量還與飲食習慣、體育鍛鍊有關，可能還與個人先天體質有關。2.商品銷售收入與廣告支出有關。商品銷售收入與廣告支出經費有著密切聯繫，但是商品銷售收入不僅與廣告 支出經費有關，還與商品質量、居民收入有關，甚至有時候與替代商品的質量和價格相關。

不過日常生活中常說的“正比”多與“正相關”混淆。 例如“收入高低與學歷高低成正比”這句話，嚴格來說是不科學的，因為找不到確定的比例係數k。當然我們都理解這句話的意思是說“學歷越高收入則越高”，嚴格來說應該這樣表述：“收入高低與學歷高低正相關”。

簡而言之，就是有直接的因果關係。

正比，有一個確定的比例係數，如正比例函式：y=2x,比例係數是2，那么，可見，

x	……	-1	0	1	2	3	……
y	……	-2	0	2	4	6

這樣，每當x增加1時，相應的y值就會增加2。這樣，每當x減少1時，相應的y值就會減少2。

更準確地說，每當x增加1時，相應的y值就會增加1的2倍。這樣，每當x減少1時，相應的y值就會減少1的2倍。

區別

正相關，只是一種概念上的，並且是基於大量的統計數據所展現出來的連個指標間的一種相互關係，而非具體兩個個體之間一定滿足這樣的同向變化關係.有這么一種趨勢和相關關係的兩個變數，因變數和自變數之間並沒有確定的數量關係，即沒有很具體和比例係數k。如身高與體重：身高增加，體重一般也會增加，但身高增加一厘米，體重可能增加1斤，也可能是2斤，甚至10斤。所以體重與身高成正相關，而不是成正比。

在函式圖形上看，正比表現為直線，有具體的線性關係；正相關則表現為向右上方傾斜的趨勢，可以是非線性的。

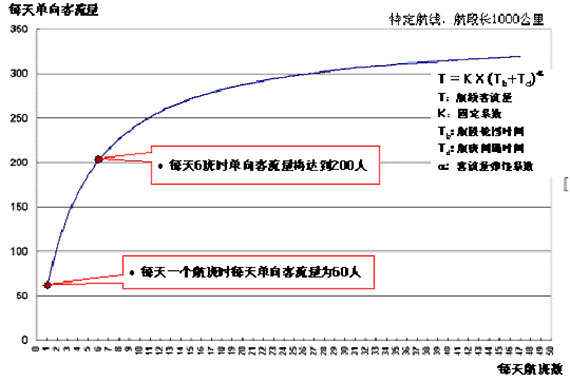
下圖就是典型的非線性正相關。

右圖可以看出，途中曲線的數值隨x增大y也隨著增大，其曲線斜率k始終大於零。

資金收益率和年限的正相關

舉例

變數關係

在一次對人體內脂肪含量與年齡關係的研究中，研究人員的出了一組樣本數據：

年齡	23	27	39	41	45	49	50	53	54	56	57	58	60	61
脂肪含量	9.5	17.8	21.2	25.9	27.5	26.3	28.2	29.6	30.2	31.4	30.8	33.5	35.2	34.6

下面便要做出散點圖（而不是函式圖象），因為從表中可以看到年齡為57的，脂肪含量並沒有增大。

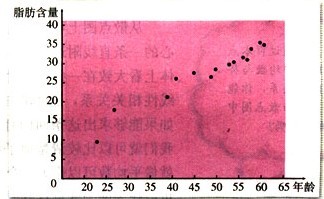
對與表中數據，我們假設人的年齡影響體內脂肪含量，於是，按照習慣，以x軸表示年齡，以y軸表示脂肪含量，得到散點圖：

這些點散布的位置也是值得注意的，它們散布在從左下角到右上角的區域。對於兩個變數的這種相關關係，我們將它稱為正相關。

線性回歸

從上面的散點圖可以看出，這些點大致分布在通過散點圖中心的一條直線附近。如果散點圖中的分布從整體上看大致有在一條直線附近，就稱這兩個變數之間具有線性相關關係，這條直線叫做回歸直線。

附：回歸直線的算法：

正相關的函式

y=kx+b(k>0)

y=x^a(x>0,a>0)

y=a^x(a>1)

(其中a>1，x>0 ）具體可參考對數函式。