基本介紹
- 中文名:正比例函式
- 外文名:directly proportional function
- 表達式:y=kx
- 提出者:Jack louny
- 提出時間:1911
- 套用學科:數學
- 適用領域範圍:生活
- 適用領域範圍:數學
定義,性質,單調性,對稱性,圖像,圖像描述,圖像作法,圖像性質,正比例,例題,
定義
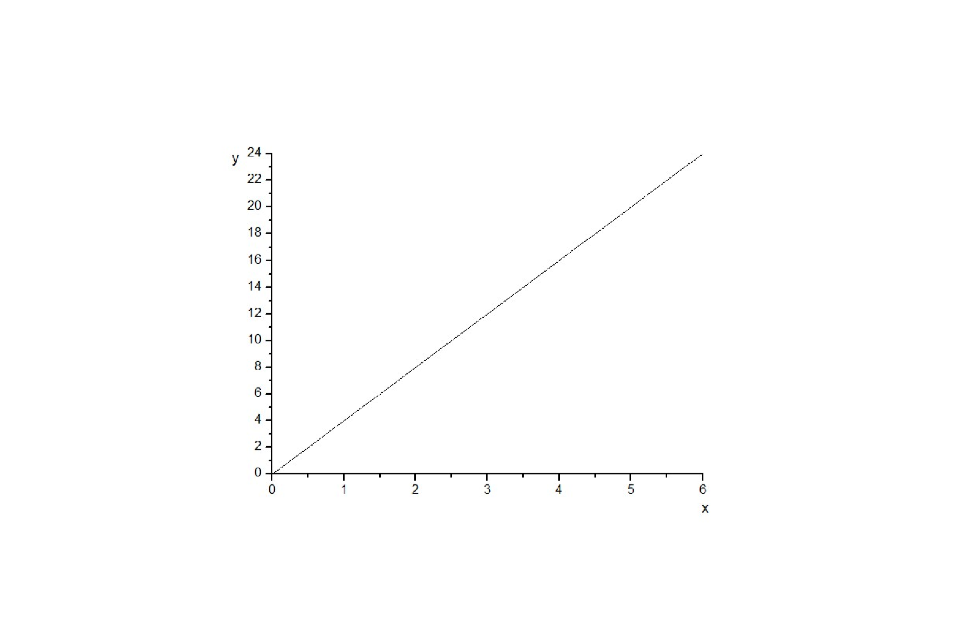
正比例函式屬於一次函式,是一次函式的一種特殊形式。即一次函式形如:y=kx+b(k為常數,且k≠0)中,當b=0時,則叫做正比例函式。 一般地,形如y=kx(k是常數,k≠0)的圖像是一條經過原點的直線,我們稱它為直線y=kx。
性質
單調性
對稱性
對稱點:關於原點成中心對稱。
對稱軸:自身所在直線;自身所在直線的垂直平分線。
圖像
圖像描述
正比例函式y=kx(k≠0),當k的絕對值越大,直線越“陡”;當k的絕對值越小,直線越“平”。
1、已知一點坐標,用待定係數法求函式解析式。先設解析式為y=kx,再代入已知點坐標,解出k的值。
2、解出k的值後,在數軸上標出各點並連線個點
圖像作法
(一)
1、在x允許的範圍內取一個值,根據解析式求出y的值;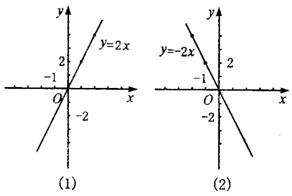 正比例函式的圖片
正比例函式的圖片
 正比例函式的圖片
正比例函式的圖片2、根據第一步求的x、y的值描出點;
3、作出第二步描出的點和原點的直線(因為兩點確定一直線)。
(二)
1、已知一點坐標,用待定係數法求函式解析式。先設解析式為y=kx,再代入已知點坐標,解出k的值;
2、解出k的值後,在數軸上標出各點並連線個點。
圖像性質
正比例函式在線性規劃問題中體現的力量也是無窮的。
還有,y=kx 是 y=k/x 的圖像的對稱軸。
正比例
②用字母表示:如果用字母x和y表示兩種相關聯的量,用k表示它們的比值,(一定)正比例關係可以用以下關係式表示: 其中k為常數。
其中k為常數。

③正比例關係兩種相關聯的量的變化規律:對於比值為正數的,即y=kx(K為常數,k≠0),此時的y與x,同時擴大,同時縮小,比值不變。例如:汽車每小時行駛的速度一定,所行的路程和所用的時間 成正比例 。以上各種商都是一定的,那么被除數和除數所表示的兩種相關聯的量成正比例關係。
注意:在判斷兩種相關聯的量是否成正比例時,應注意這兩種相關聯的量,雖然也是一種量隨著另一種的變化而變化,但它們相對應的兩個數的比值不一定,那它們就不能成正比例。例如:一個人的年齡和它的體重,就不能成正比例關係,正方形的邊長和它的面積也不成正比例關係。 而單價數量與總價是成正比的(單價不變,總價隨著數量的增減而增減)。
例題
首先通過5個問題,得出5個函式,觀察這5個函式,可納出正比例函式概念。
根據上面的5個實際問題,我們得到5個函式。下面觀察這5個函式的共同點,以便歸納出正比例函式概念。
①h=2t ;② m=7.8n; ③s=0.5t; ④T=t/3 ;⑤y=200x。
這5個函式有什麼共同的特點?
1:都有自變數。
2:都是函式。
3:都有常量。
這5個函式的右邊都是常量和自變數的什麼形式?
這5個函式都是常量與自變數的乘積形式,都可表達為y=kx(k不等於0)的形式。
下面是4個函式,請判斷哪些是正比例函式?
①y=3; ②y=2x; ③y=1/x; ④y=x^2。
解答: