完全相關是指兩個變數之間的關係,一個變數的數量變化由另一個變數的數量變化唯一確定。其相關係數為+1或-1。
基本介紹
- 中文名:完全相關
- 外文名:Completely related
- 拼音:Wán quán xiāng guān
- 學科:數學
- 隸屬:科學
- 歸類:相關關係的一種
基本內容
比較
表示

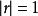
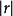
相關例題
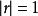

完全相關是指兩個變數之間的關係,一個變數的數量變化由另一個變數的數量變化唯一確定。其相關係數為+1或-1。

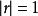
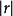
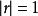
完全相關是指兩個變數之間的關係,一個變數的數量變化由另一個變數的數量變化唯一確定。其相關係數為+1或-1。...
相關係數是變數之間相關程度的指標。樣本相關係數用r表示,總體相關係數用ρ表示,相關係數的取值一般介於-1~1之間。...
不完全相關,兩個現象之間的關係介乎完全相關與不相關之間的關係,一般所說的相關就是指不完全相關參見〔相關〕、〔不相關〕、〔完全相關〕。 ...
簡稱全相關係數。 ...... 完全相關係數編輯 鎖定 本詞條缺少信息欄、名片圖,補充相關內容使詞條更完整,還能快速升級,趕緊來編輯吧!簡稱全相關係數。 [1] ...
完全性,即完備性。在數學及其相關領域中,一個對象具有完備性,即它不需要添加任何其他元素,這個對象也可稱為完備的或完全的。更精確地,可以從多個不同的角度來...
相關係數是最早由統計學家卡爾·皮爾遜設計的統計指標,是研究變數之間線性相關程度的量,一般用字母 r 表示。由於研究對象的不同,相關係數有多種定義方式,較為常用...
在圖論的數學領域,完全圖是一個簡單的無向圖,其中每對不同的頂點之間都恰連有一條邊相連。完整的有向圖又是一個有向圖,其中每對不同的頂點通過一對唯一的...
相關圖是研究相關關係的直觀工具。一般在進行詳細的定量分析之前,可利用相關圖對現象之間存在的相關關係的方向、形式和密切程度進行大致的判斷。相關圖又稱散點圖或...
完全變態發育是昆蟲變態的兩種類型之一。昆蟲在個體發育中,經過卵、幼蟲、蛹和成蟲等4個時期的叫完全變態。昆蟲在個體發育中,只經過卵、幼蟲和成蟲等3個時期的,...
完全彈性碰撞(Perfect Elastic Collision) 在理想情況下,完全彈性碰撞的物理過程滿足動量守恆和能量守恆。一般在高中物理教材上,直接稱這樣滿足機械能守恆與動量守恆的...
完全可約表示(completely reducible representation)是指可完全分解為不可約表示的一種表示。設ρ:G→GL(V)是G的一種表示,若V=V1⊕…⊕Vm使每個Vi均為ρ(G)...
完全信息是一個出現在經濟領域和博弈論中的術語,它用來描述一種經濟現象或博弈現象,即對於所有參與者來說都能夠了解到其他市場參與者的一切信息。每個博弈者都能...
在數學中,有向完全偏序和完全偏序是兩種特殊的偏序集合,分別簡寫為 dcpo 和 cpo。它們特徵化自特定的完備性性質。dcpos 和 cpos 是序理論的概念,主要套用於理論...
中國《民法總則》規定:十八周歲以上的自然人為成年人。成年人為完全民事行為能力人,可以獨立實施民事法律行為。十六周歲以上的未成年人,以自己的勞動收入為主要生活...
完全歸納推理,又稱“完全歸納法”,它是以某類中每一對象(或子類)都具有或不具有某一屬性為前提,推出以該類對象全部具有或不具有該屬性為結論的歸納推理。...
