概念解釋
偏相關是地理系統的一個多要素系統,一個要素的變化要影響到其它要素的變化,因此它們之間存在著不同的相關關係。兩個要素同時消除了其餘要素影響後的相關,稱為偏相關。偏相關係數是度量偏相關程度和方向的指標,它可以通過相關係數法來計算。設有三個要素或變數x1,x2,x3,其單相關係數矩陣如下圖。
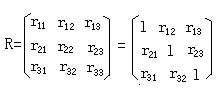 圖1.
圖1.因是對稱相關矩陣,故只需計算出 r12、r13、r23,三個變數間的偏相關係數有三個,即 r12·3, r13·2,r23·1(下標圓點後面的數字,代表保持不變的變數,如 r12·3表示 x3 保持不變),稱為一級偏相關係數。若有四個要素或變數相關,則有六個偏相關係數,即 r12·34,r13·24,r14·23,r23·14,r24·13,r34·12 ,稱為二級偏相關係數。要素或變數多於四個時,可以類推。
性質
偏相關係數γ12·34…n的性質為:
①偏相關係數的取值範圍為 -1≤γ12·34…n≤1。
②γ12·34…n為正值,表示當x3,x4,…,xn不變的情況下,x1與x2為正相關關係; r12·34…n為負值,表示當x3,x4, …,xn不變的情況下,x1與x2為負相關關係。
③偏相關係數的絕對值越大,其偏相關程度就越密切。當 |γ12·34…n|=1時,表示當x3,x4, …xn不變的情況下,x1與x2為完全相關; 當γ12·34…n= 0時,表示當 x3,x4,…,xn不變的情況下,x1與x2為完全不相關。
④偏相關係數的絕對值必小於、最多等於由同一資料計算的復相關係數,如R1·23≧ |γ12·3|。
⑤偏相關係數右下角前部數字位置可任意互換,其值不變,如 γ12·3=γ21·3,γ13·24=γ31·24等。
作用
偏相關分析的主要作用在於,在所有的自變數中,判斷哪些自變數對因變數的影響較大,從而選擇作為必需的自變數,至於那些對因變數影響較小的自變數就可以捨去而不予考慮。這樣,在計算多元回歸方程時,只要保留起主要作用的自變數,用較少的自變數描述因變數的平均變動量。
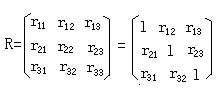 圖1.
圖1.
