基本介紹
- 中文名:相對標準偏差
- 外文名:relative standard deviation
- 符號表示:RSD
- 別稱:標準偏差係數、變異係數
- 所屬學科:數學(統計學)
基本介紹

相關概念
平均值
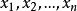


標準偏差



套用舉例








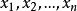











相對標準偏差(relative standard deviation;RSD)又叫標準偏差係數、變異係數、變動係數等,由標準偏差除以相應的平均值乘100%所得值,可在檢驗檢測工作中分析結果的精密...
絕對偏差平均偏差 指各次測量值的絕對偏差絕對值的平均值。絕對偏差相對平均偏差 指平均偏差占平均值的百分率。絕對偏差標準偏差 指多次平行測定值(測定次數或樣本數...
例:分析鐵礦石中鐵的質量分數,得到如下數據:37.45,37.20,37.50,37.30,37.25(%),計算測結果的平均值、平均偏差、相對平均偏差、標準偏差。...
標準偏差反映數值相對於平均值 (mean) 的離散程度。偏差變數各學科里的定義 編輯 偏差變數幾何量偏差 孔軸的標準公差等級為分為20個等級。...
相對標準偏差(RSD,relative standard deviation)就是指:標準偏差與測量結果算術平均值的比值,即: 相對標準偏差(RSD)=標準偏差(SD)/計算結果的算術平均值(X) 該值...
standard deviation 標準偏差relative standard deviation 相對標準偏差;相對標準差deviation angle 偏向角frequency deviation 頻率偏移absolute deviation 絕對偏差...
最佳測定範圍應小於方法的適用範圍。對測量結果的精密度(通常以相對標準偏差表示)要求越高,相應的最佳測定範圍最小。V百科往期回顧 詞條統計 瀏覽次數:次 編輯次數...
選用酸價值較高的樣品,分別用自動電位滴定法和人工滴定法平行測定5次,自動電位滴定法測定的相對標準偏差1.1%,人工滴定法為1.6%;平行測定酸價值較低的樣品5次,...
其檢出限的數量級為ng/g~pg/g,相對標準偏差小於30%,線性範圍為3一5個數量級。固相微萃取技術的主要優點是:不用或少用溶劑;操作簡便;易於自動化和與其他技術...
對標準含量為1.50和2.00 mg/L的DNA,6次測定結果分別為1.52和2.08 mg/L,相對標準偏差分別為3.1%和2.5%;對標準含量為4.00和5.00 mg/L的RNA,6次測定...
