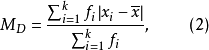基本介紹
- 中文名:絕對偏差
- 外文名:absolute deviation
- 定義:某一觀測值與觀測值的均值之差
- 所屬學科:數學(統計學)
- 相關概念:平均絕對偏差
- 簡稱:偏差
基本介紹,相關概念,平均偏差,相對平均偏差,標準偏差,相對標準偏差,差方和,方差,平均絕對離差,
基本介紹
當我們進行任一測量時,由於測量設備、測量方法、測量環境、人的觀察力和被測對象等,都不能做到完美無缺,而使測量結果受到歪曲,表現為測量結果與待測量真值間存在一定差值,這個差值就是測量誤差。
由此可知,誤差是不能完全消除的,只能減小和削弱,這也正是我們研究誤差理論的主要目的。
表示誤差的常用方法有以下幾種:
(2)絕對偏差和相對偏差;
(3)平均偏差和相對平均偏差;
(4)極差;
絕對誤差是測量值(單一測量值或多次測量值的均值)與真值之差。測量結果大於真值時,誤差為正,反之為負。
相對誤差為絕對誤差與真值的比值(常以百分數表示)。
絕對偏差為某一測量值與多次測量值的均值之差。
相對偏差為絕對偏差與均值的比值(常以百分數表示)。
極差為一組測量值中最大值與最小值之差。又稱範圍誤差或全距,以R表示,即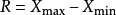 。
。
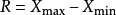
相關概念
平均偏差
指各次測量值的絕對偏差絕對值的平均值。

相對平均偏差
指平均偏差占平均值的百分率。
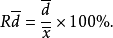
標準偏差
指多次平行測定值(測定次數或樣本數n≤20)偏離平均值的距離的平均數,它是方差的算術平方根,其計算公式如下:



總體標準偏差,符號為 ,其計算公式如下:
,其計算公式如下:

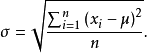
相對標準偏差
指標準偏差占平均值的百分率,又稱為變異係數(CV),通常用RSD表示。

差方和
樣本差方和:

方差
樣本方差:

平均絕對離差
平均絕對離差(mean absolute deviation)是用樣本數據相對於其平均值的絕對距離來度量數據的離散程度。平均絕對離差也稱為平均離差(mean deviation)。平均絕對離差定義為各數據與平均值的離差的絕對值的平均數。
設樣本的n個觀測值為 ,平均絕對離差為:
,平均絕對離差為:


對於分組數據,平均絕對離差為: