完全可約表示(completely reducible representation)是指可完全分解為不可約表示的一種表示。設ρ:G→GL(V)是G的一種表示,若V=V1⊕…⊕Vm使每個Vi均為ρ(G)不變子空間且Vi對應G的不可約表示,則稱ρ為完全可約表示。
基本介紹
- 中文名:完全可約表示
- 外文名:completely reducible representation
- 提出者:弗羅貝尼烏斯
- 所屬學科:數學
- 所屬問題:群及其推廣(群表示論)
基本介紹

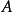
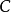
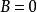
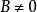
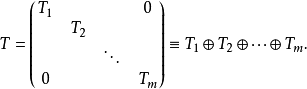
相關結論
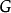
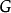
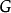
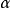
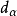
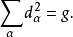
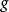
概念的提出與群表示論
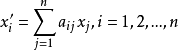

完全可約表示(completely reducible representation)是指可完全分解為不可約表示的一種表示。設ρ:G→GL(V)是G的一種表示,若V=V1⊕…⊕Vm使每個Vi均為ρ(G)不變子空間且Vi對應G的不可約表示,則稱ρ為完全可約表示。

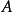
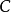
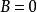
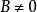
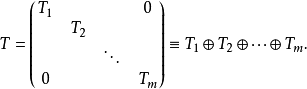
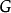
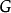
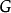
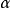
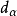
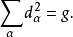
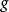
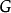
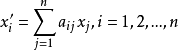
完全可約表示(completely reducible representation)是指可完全分解為不可約表示的一種表示。設ρ:G→GL(V)是G的一種表示,若V=V1⊕…⊕Vm使每個Vi均為ρ(G)...
若除X和{0}外不存在其他不變子空間,則稱此表示為巴拿赫代數的不可約表示。...... 若除X和{0}外不存在其他不變子空間,則稱此表示為巴拿赫代數的不可約表示...
絕對不可約表示是域擴張之下保持不可約性的線性表示。若P是群G的一個F表示,K是F的擴域,則P也可以看成一個K表示。若對F'的任一個擴域K,p均為不可約K...
《辮子群的不可約表示》是仝殿民編寫的理論物理學科論文。...... 《辮子群的不可約表示》是仝殿民編寫的理論物理學科論文。副題名外文題名Irreducible Representations...
第三章 完全轉動群的不可約表示和角動量 3.1 用歐拉角描述轉動的完全轉動群的不可約表示 3.2 二維么正群 …… 第四章 群論在有關原子結構問題中的套用 第五...
卡西米爾運算元的個數等於群的秩,它們一起構成一個完全組。卡西米爾運算元的重要性在於,這組運算元的本徵值可用來標記群的不可約表示,即它們的每一組本徵值都代表了...
§5.6表示DJ的矩陣元§5.7不可約表示DJ的性質§5.8旋轉群的乘積表示§5.9乘積表示分解的具體方法§5.10完全的三維正交群的表示第六章旋轉群表示的套用...
§3.2 完全轉動群SO(3)的不可約表示§3.3 二維麼模么正群SU(2)§3.4 SU(2)群的不可約表示§3.5 雙群習題第四章 點群及其套用...
1 三維單純李代數的不可約表示2 SU(2)的不可約酉表示3 S0(3,R)的不可約酉表示4 半單純李代數的不可約表示5 完全可約性定理習題...
舒爾指數(Schur index)是將子域的特徵標看成擴域的特徵標時,刻畫分解程度的一類數量。若F是一個域,E是F的擴域,ρ是群G的一個不可約E表示,則存在G的一個...
● 半單若且唯若每個g的表示都是完全可約的。半單李代數的另一個重要性質是[g,g]=g,其逆未必成立。半單李代數李代數 編輯 ...
如果用m1、m2表示兩個物體的質量,r表示它們間的...兩個可看作質點的物體之間的萬有引力,可以用以下公式...其中G代表引力常量,其值約為6.67×10-11 N·m2 ...
存在消相干子空間條件 13.3.2 系統一環境相互作用不具有完全對稱性情況下存在...正則表示 A3.1.3 等價表示、么正表示定理 A3.1.4 可約表示、不可約表示 A...
3.6 表示論的基本問題 3.7 最基本的表示 3.8 不可約表示的分類 3.9 研究方法...7.6 不完全性篇:橫看成嶺側成峰,遠近高低各不同 7.7 非標準模型篇:不識...
