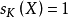舒爾指數(Schur index)是將子域的特徵標看成擴域的特徵標時,刻畫分解程度的一類數量。若F是一個域,E是F的擴域,ρ是群G的一個不可約E表示,則存在G的一個不可約F表示ζ使ρ是ζE的不可約成分,其中ζE是將ζ看做E表示。進而,若G的兩個不可約F表示ζ1,ζ2使ζE1與ζE 都有不可約成分ρ,則ζ1與ζ2是等價表示。下面假定χ是G的一個不可約E特徵標,對應表示ρ,F是E的一個子域,ζ是G的一個不可約F表示使得ρ為ζE的不可約成分,這時定義χ在F上的舒爾指數為ρ在ζE中的重數,記為mF(χ)。由於前述原因,舒爾指數是一個確定的正整數。利用舒爾指數可以測度一個不可約E特徵標是否是其子域F上的特徵標。
基本介紹
- 中文名:舒爾指數
- 外文名:Schur index
- 所屬學科:數學
- 所屬問題:群表示論/結合代數
- 提出者:舒爾
定義,相關定理,舒爾簡介,
定義
舒爾指數(Schur index)是指與有限中心單代數相似的可除代數的次數。對域F上有限維中心單代數A,從同構意義上來說存在惟一中心可除代數D和某自然數n,使得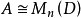 。將相應於A的可除代數D的次數
。將相應於A的可除代數D的次數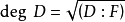 稱為A的舒爾指數,記為
稱為A的舒爾指數,記為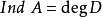 。舒爾指數也可對任意可分代數定義,特別地,有限維半單代數
。舒爾指數也可對任意可分代數定義,特別地,有限維半單代數 ,若對每個單代數
,若對每個單代數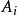 的舒爾指數定義為
的舒爾指數定義為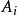 作為它中心上代數的舒爾指數
作為它中心上代數的舒爾指數 ,則
,則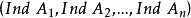 就稱為A的舒爾指數。
就稱為A的舒爾指數。
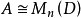
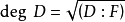
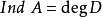

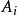
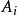

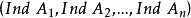
相關定理
設 為
為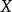 在
在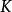 上的舒爾指數,並記為
上的舒爾指數,並記為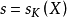 。
。

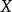
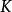
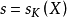
定理2 設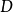 為
為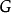 的一個絕對不可約表示,其指標為
的一個絕對不可約表示,其指標為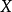 。
。
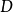
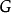
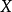
a) 若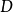 可以在
可以在 的某擴域
的某擴域 上實現,並且
上實現,並且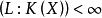 ,則舒爾指數
,則舒爾指數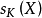 是
是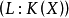 的因子。
的因子。


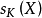
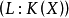
b) 存在 的一個擴域
的一個擴域 ,使
,使 ,而且
,而且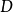 可在
可在 上實現。
上實現。



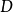

c) 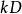 在
在 上可實現若且唯若
上可實現若且唯若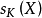 是k的因子。
是k的因子。
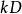

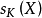
d) 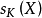 是
是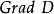 的因子。
的因子。
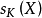
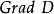
定理3設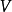 為不可約
為不可約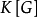 -模,
-模, 為
為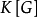 的分裂域而
的分裂域而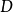 為
為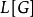 在
在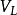 上的表示
上的表示 的絕對不可約分量,那么,
的絕對不可約分量,那么, 是完全可約的,它的絕對不可約分量就是全體在K與D共軛的表示
是完全可約的,它的絕對不可約分量就是全體在K與D共軛的表示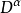 ,而且每一個等價類都以相同的重數s出現,若
,而且每一個等價類都以相同的重數s出現,若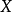 為D的指標,則s等於
為D的指標,則s等於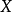 在
在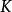 上的舒爾指數
上的舒爾指數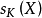 ,若
,若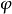 為
為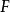 的指標,則
的指標,則
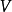
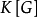

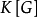
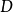
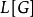
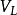


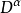
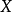
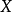
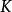
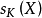
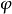
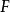
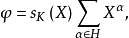
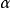


定理4設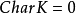 ,而
,而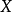 為
為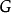 在
在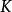 的某擴域
的某擴域 上的絕對不可約指標。
上的絕對不可約指標。
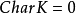
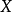
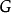
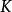

a) 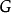 恰有一個在
恰有一個在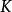 上的不可約指標
上的不可約指標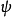 ,使
,使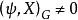 ,這裡
,這裡 ,此處H為
,此處H為 在
在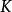 上的伽羅華群。
上的伽羅華群。
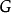
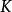
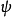
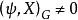


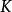
b) 若 為
為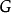 在
在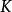 上的指標,則
上的指標,則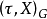 總能被舒爾指數整除。
總能被舒爾指數整除。

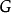
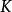
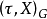
舒爾簡介
舒爾(Schur,Issai,1875.1.10-1941.1.10)是德國數學家。生於俄國莫吉廖夫,卒於巴勒斯坦特拉維夫(現屬以色列)。曾在柏林大學讀過書。1911年執教於波恩,1919年任柏林大學數學教授。1935年受納粹當局迫害離職,1939年移居巴勒斯坦。舒爾是當時德國最優秀的猶太數學家之一,他追隨其師弗羅貝尼烏斯研究群的表示理論,以發現“舒爾函式”和證明“舒爾定理”而著稱。他第一個通過線性函式變換來研究所謂“表示”,並首先在代數數域問題上使用了“舒爾指數”,還重建了群的特徵理論(1905年)。此外,他對群論、矩陣理論、代數方程論、數論、級數理論、積分方程和函式論等領域均有論述。舒爾的研究工作對現代數學的發展有很大影響。1973年,德國著名的施普林格出版社出版了他的論文集。