簡介
光譜學是一門主要涉及物理學及化學的重要交叉學科,通過
光譜來研究
電磁波與物質之間的
相互作用。光是一種由各種
波長(或者頻率)的電磁波疊加起來的
電磁輻射。光譜是一類藉助
光柵、
稜鏡、
傅立葉變換等分光手段將一束電磁輻射的某項性質解析成此
輻射的各個組成波長對此性質的貢獻的圖表。例如一幅
吸收光譜可以在某個
波段按照從低到高的波長順序列出物質對於相應波長的吸收程度。
隨著科技的進展,光譜學所涉及的電磁波波段越來越寬廣,從波長處於
皮米級的
γ射線,到
X射線,
紫外線,
可見光區域,
紅外線,微波,再到波長可達幾公里的
無線電波,都有其與物質作用的特徵形式。按照光與物質的作用形式,光譜一般可分為
吸收光譜、
發射光譜、散射光譜等。通過光譜學研究,人們可以解析
原子與
分子的
能級與幾何結構、特定化學過程的
反應速率、某物質在
太空中特定區域的濃度分布等多方面的微觀與巨觀性質。人們也可以利用物質的特定組成結構來產生具有特殊光學性質的光譜,例如特定頻率的雷射。光譜學並不僅是一門基礎科學,在日常套用中它也是一種重要的定性、定量測量方法,例如水質中各項物質含量的分析、通過分析血液中蛋白質的含量進行疾病預防與監測、使用最優波段進行光纖通訊等。自上世紀中葉雷射被發現以來,人類對於光的控制達到了新的階段,可以產生具有前所未有的亮度、頻率分布以及時間解析度的電磁輻射,開啟了通向
非線性光學與非線性光譜學的大門,使得光譜學處於高速發展的嶄新時期。
簡史
光譜學的研究已有三百多年的歷史了。1666年,
I.牛頓把通過玻璃稜鏡的
太陽光展成從紅光到紫光的各種顏色的光譜,他發現白光是由各種顏色的光組成的。這是最早對光譜的研究。其後一直到1802年,W.H.渥拉斯頓與1814年 J.von
夫琅和費彼此獨立地觀察到了
光譜線。每條譜線只代表一種“顏色”的光。這裡顏色一詞是廣義的。牛頓之所以沒有能觀察到光譜線,是因為他使太陽光通過了圓孔而不是通過狹縫。在1814~1815年之間,
夫琅和費公布了
太陽光譜中的許多條暗線,並以字母來命名,其中有些命名沿用至今。此後便把這些線稱為
夫琅和費暗線。
 光譜學
光譜學實用光譜學是由基爾霍夫,G·R與
本生,R·W.E.在19世紀60年代發展起來的;他們證明光譜學可以用作定性
化學分析的新方法,還利用這種方法發現了幾種當時還為人所不知的元素,並且證明了在太陽里存在著多種已知的元素。
從19世紀中葉起一直是光譜學研究的重要課題之一。在試圖說明
氫原子光譜的過程中,所得到的各項成就對
量子力學法則的建立起了很大
促進作用。這些法則不僅能夠套用於氫
原子,也能套用於其他原子、分子和
凝聚態物質。事實上,它們終於成為近代化學、固體物理乃至套用學科諸如
電子學的基礎。
氫原子光譜中最強的一條譜線是1853年由
瑞典物理學家A.J.
埃斯特朗探測出來的(
光波波長的單位即以他的姓氏命名,1埃等於10-8厘米)。此後的20年中,在星體的光譜中觀測到了更多的氫原子譜線。1885年,從事
天文測量的
瑞士科學家J.J.
巴耳末找到一個經驗公式來說明已知的氫原子譜線的位置。此後便把這一組線稱為
巴耳末系。繼巴耳末的成就之後,1889年,瑞典光譜學家J.R.
里德伯發現了許多元素的線狀光譜系,其中最為明顯的為
鹼金屬原子的光譜系,它們都能滿足一個簡單的公式——
里德伯公式。這個公式後來寫成
(1)1/λ=R[(1/m2)-(1/n2)]+bn+c
其中
λ為波長,以埃為單位。
m和
n取正整數1,2,3,…。
b和с為常數,其數值依賴於不同元素不同線系。
R的值對於所有元素的線系都幾乎相同,稱為
里德伯常量。當式(1)中的
b,с都等於零時,則式(1)簡化為
巴耳末公式。
1/λ=R[(1/m2)-(1/n2)](2)
以適當的m和n的值代入式(2)中,就得到了氫原子光譜中所有譜線的波長。
儘管氫原子光譜線的波長的表示式(2)十分簡單,但對其起因當時卻茫然不知。一直到1913年,N.
玻爾才對它作出了明確的解釋。玻爾不僅導出式(2),而且也計算出里德伯常數的數值。雖然
玻爾理論在概念上比以前有了很大進展,但玻爾理論並不能解釋所觀測到的原子光譜的各種特徵,即使對於氫原子光譜的進一步的解釋也遇到了困難。例如,早在1892年A.A.
邁克耳孫就發現了巴耳末系中的最強線實際上是由緊靠近的兩條線組成的,它們之間的間隔約為0.14埃。
能夠滿意地解釋這種光譜線的分裂以及其他
複雜原子光譜的是20世紀發展起來的量子力學。電子不僅具有軌道角動量,而且還具有
自旋角動量。這兩種角動量的結合便成功地解釋了光譜線的分裂現象。
電子自旋的概念首先是在1925年由G.E.
烏倫貝克和S.A.
古茲密特作為假設而引入的,以便解釋
鹼金屬原子光譜的
測量結果。在P.A.M.
狄拉克的相對論性量子力學中,電子自旋(包括
質子自旋與
中子自旋)的概念有了牢固的理論基礎,這乃是基本方程的自然結果而不是作為一種特別的假設了。
1896年,P.
塞曼把光源放在
磁場中來觀察磁場對光譜線的影響。結果發現所研究的光譜線分裂成為密集的三重線,而且這些譜線都是偏振的。現代把這種現象稱為
塞曼效應。1897年,H.A.
洛倫茲對於這個效應作了滿意的解釋,其基本概念是光由
各向同性的
諧振子發射出來的,這些諧振子的運動在磁場中受到了
磁力線的作用,產生了塞曼分裂。但是,1898年,T.普雷斯頓觀察到鋅線(4722埃)與
鎘線(4800埃)在磁場中分裂為四重線而非三重線。類似的現象別人也觀察到了。後來人們便把
譜線的三重線分裂稱為正常塞曼效應,而把所有例外情況稱為
反常塞曼效應。
塞曼效應不僅在理論上具有重要意義,而且在實用上也是重要的,在複雜光譜的分類中,塞曼效應是一種很有用的方法,有效地幫助了人們對於複雜光譜的理解。另一方面,被稱為
斯塔克效應的光譜線在
電場中的分裂(1913)則僅具有理論意義,而對於光譜線的分析卻無實際用途。
內容
根據研究光譜方法的不同,習慣上把光譜學區分為
發射光譜學、吸收光譜學與
散射光譜學。這些不同種類的光譜學從不同方面提供物質微觀結構知識及不同的化學分析方法。
發射光譜學
發射光譜可以區分為三種不同類別的光譜:
線狀光譜、帶狀光譜和
連續光譜。線狀光譜主要產生於原子,帶狀光譜主要產生於分子,連續光譜則主要產生於
白熾的固體或氣體放電。
現代觀測到的原子發射的光譜線已有百萬條了。每種原子都有其獨特的光譜,猶如人的
指紋一樣是各不相同的。根據光譜學的理論,每種原子都有其自身的一系列分立的能態,每一能態都有一定的能量。以氫原子為例,能量的大小可表示為(3)
式中
n取從1到
∞的正整數,稱為主量子數,從經典的觀點來說,
n是描寫電子圍繞原子核運動的軌道的大小的。每一個
n值也就決定了一個能級。
RH為氫原子的里德伯常數。
h為
普朗克常數。公式中的負號是因為習慣上把相應於
n=
∞的能量定為最高值並令它等於零,而相應於
n=1的能量則定為最低能量,這個能態稱為
基態,相應的
能級稱為基能級。當原子以某種方法從基態被提升到較高的能態上時,原子的內部能量增加了,原子就會把這種多餘的能量以光的形式發射出來,於是產生了原子的
發射光譜。原子發射出來的光的頻率
v為 ,(4)
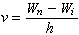 光譜學
光譜學式中
Wh為較高能級的能量,
Wi為較低能級的能量。頻率經常以厘米倒數(cm
-1)來量度;1厘米倒數是在1cm長度內所包括的波長數目。在細緻地描寫原子中的電子運動時,除了主量子數
n以外,還有另外三個量子數,分別以
l、
m和
s表示。
l是描寫電子軌道運動角動量的大小的,稱為
角量子數,它的值取(
n-1)到0之間的正整數。
l=0的電子稱為s電子,
l=1的電子為p電子,
l=2的電子為d電子等。量子數
m是描寫電子的運動軌道在空間的取向的,稱為
磁量子數,它的值不能大於
l但可以為負。對於給定
l來說,
m=
l,
l-1,…,-
l。
s為電子自旋量子數,是描寫電子自旋的角動量的,等。它產生出光譜中的多重線。如果原子中產生光譜的電子不只一個時,各個電子的自旋的矢量和
S為電子組態的總自旋。
量子數S永遠是正數。對於軌道角動量也是如此,它們的和給出原子的總軌道角動量(量子數為
L)。
L=0時,有關的能態稱為S態;
L=1時,稱為P態;
L=2時,稱為D態等。多電子
原子能級的高低依賴於
S,依賴於
L,也依賴於
S與
L之間的相互作用。
S與
L結合在一起給出原子的總角動量
J。量子數
J取正值,其範圍在
L與
S之差的最小值和
L+
S的最大值之間。在光譜學中,常常以符號MLJ來表示原子的能級或者光譜項。其中
M=2
S+1為光譜的多重性,是表示能級分裂的數目的。例,則
M=2,這意味著每個能級(S能級除外)都分裂成兩個成分,鹼金屬原子能級就屬於這種情況。對於兩個電子的原子而言,
S=0或1,這取決於兩電子的自旋方向是平行的還是反平行,因之能級的多重性或者為1(能級無分裂)或者為3(每一能級分裂成三個成分)。
鹼土金屬原子的能級就屬於這種情況。依次類推。原子在各能級之間的躍遷就產生出光譜線來,從高能級向低能級的躍遷產生髮射光譜;反之,產生吸收光譜。根據量子力學的法則,原子在能級之間的躍遷是遵守選擇定則的,這些選擇定則為 Δ
L=0,±1;Δ
S=0;Δ
J=0(除了
J=0),±1。符號Δ
L表示躍遷中的初態與終態的
L值之差。Δ
S和Δ
J的意義同此。
 光譜學
光譜學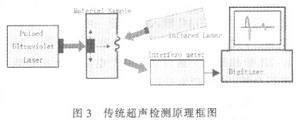 光譜學
光譜學 光譜學
光譜學在分子的發射光譜中,研究的主要內容是二原子分子的發射光譜在分子中,電子圍繞著兩個或多個
原子核運動,像原子一樣,每種運動都有其特定的
能級。除了電子運動之外,原子核圍繞其中心彼此作
周期振動;此外,這些原子核作為整體也會圍繞某些軸在空間轉動。所有這些運動都會顯示在分子光譜中,因而分子光譜就變得十分複雜了。
分子中的電子,像原子中的電子一樣有四個量子數。但在二原子分子中,電子為兩個原子核所共有,因而量子數m
就由一個新的量子數
λ來代替了。
λ表示電子軌道對於分子軸的取向,它可以為正值也可以為負值,但在數值上不能大於
l。在二原子分子中,
λ同
自旋s的結合很相似於原子中的
l與
s的結合。它們結合在一起的代數和表示電子的總角動量在分子軸上的投影,其數值由
Λ表示,
Λ=0,1,2,…。相應於
Λ的不同的值的電子態分別由大寫的希臘字母Σ、∏、Δ、Ф、…表示。分子能態的符號同原子相似為
MΛ,
M仍等於2
S+1。例如H
2、N
2、HCl等的最低電子態為1Σ,O
2的為3Σ,NO的為2∏等。在分子中,電子態的能量比振動態的能量大50~100倍,而振動態的能量比轉動態的能量大50~100倍。因此,在分子的電子態之間的躍遷中,總是伴隨著振動躍遷和轉動躍遷的,因而許多光譜線就密集在一起而形成帶狀光譜。
 光譜學
光譜學吸收光譜學
當一束具有連續波長的光通過一種物質時,光束中的某些成分便會有所減弱,當經過物質而被吸收的光束由光譜儀展成光譜時,就得到該物質的吸收光譜。幾乎所有物質都有其獨特的吸收光譜。原子的吸收光譜所給出的有關能級結構的知識同發射光譜所給出的是互為補充的。
一般來說,吸收光譜學所研究的是物質吸收了那些波長的光,吸收的程度如何,為什麼會有吸收等問題。研究的對象基本上為分子。
吸收光譜的
光譜範圍是很廣闊的,大約從10nm到1000μm。在200
nm到800nm的光譜範圍內,可以觀測到固體、液體和溶液的吸收,這些吸收有的是連續的,稱為一般吸收光譜;有的顯示出一個或多個
吸收帶,稱為選擇吸收光譜。所有這些光譜都是由於分子的電子態的變化而產生的。
選擇吸收光譜在有機化學中有廣泛的套用,包括對化合物的鑑定、化學過程的控制、分子結構的確定、定性和
定量化學分析等。分子的紅外吸收光譜一般是研究分子的
振動光譜與
轉動光譜的,其中分子振動光譜一直是主要的研究課題。
 光譜學
光譜學分子振動光譜的研究表明,許多振動頻率基本上是分子內部的某些很小的原子團的振動頻率,並且這些頻率就是這些
原子團的特徵,而不管分子的其餘的成分如何。這很像可見光區域色基的吸收光譜,這一事實在分子紅外吸收光譜的套用中是很重要的。多年來都用來研究多原子分子結構、分子的定量及定性分析等。
在散射光譜學中,拉曼光譜學是最為普遍的光譜學技術。當光通過物質時,除了光的透射和光的吸收外,還觀測到
光的散射。在散射光中除了包括原來的入射光的頻率外(瑞利散射和廷德耳散射),還包括一些新的頻率。這種產生新頻率的散射稱為喇曼散射,其光譜稱為拉曼光譜。
拉曼散射的強度是極小的,大約為
瑞利散射的千分之一。拉曼頻率及強度、
偏振等標誌著
散射物質的性質。從這些資料可以導出物質結構及物質組成成分的知識。這就是拉曼光譜具有廣泛套用的原因。
由於拉曼散射非常弱,所以一直到1928年才被印度物理學家拉曼等所發現。他們在用汞燈的
單色光來照射某些液體時,在液體的散射光中觀測到了頻率低於入射光頻率的新譜線。在拉曼等人宣布了他們的發現的幾個月後,蘇聯物理學家蘭茨見格等也獨立地報導了晶體中的這種效應的存在。
 光譜學
光譜學拉曼效應起源於分子振動(和
點陣振動)與轉動,因此從拉曼光譜中可以得到分子
振動能級(點陣振動能級)與
轉動能級結構的知識。
拉曼散射強度是十分微弱的,在雷射器出現之前,為了得到一幅完善的光譜,往往很費時間。自從雷射器得到發展以後,利用雷射器作為激發光源,拉曼光譜學技術發生了很大的變革。雷射器輸出的雷射具有很好的單色性、方向性,且強度很大,因而它們成為獲得拉曼光譜的近乎理想的光源,特別是連續波
氬離子
雷射器與氨離子雷射器。於是拉曼光譜學的研究又變得非常活躍了,其研究範圍也有了很大的擴展。除擴大了所研究的物質的品種以外,在研究燃燒過程、探測環境污染、分析各種材料等方面拉曼光譜技術也已成為很有用的工具。
束箔光譜學
束箔光譜學是21世紀國際上發展起來的一門新興學科。主要內容是,用被加速的離子撞擊不同元素的薄箔的方法研究基礎原子物理學、測量
電子能級的平均壽命。現代國際上已有很多人將
加速器改裝用來研究束箔問題。能量在10
2~10
3eV範圍的束箔實驗可以揭示被加速的元素低
電離的電子特性,高達8~10MeV/核子的範圍可以產生高
Z的單電子和雙
電子系統的躍遷,這種躍遷可靈敏地檢驗
量子電動力學。束箔技術套用於
天體物理問題上,可以對
日冕的性質以及
銀河系中元素的豐度得到很好的理解。
 光譜學
光譜學從事原子物理學、光譜學、
天體物理學等研究工作的實驗學家和理論學家閱讀本書會獲得很多原子系統的豐富信息。大學物理系的師生和研究生閱讀本書,亦會受益。
光聲光譜學
以光聲效應為基礎的一種新型光譜分析檢測技術。用一束強度可調製的單色光照射到密封於光聲池中的樣品上,樣品吸收
光能,並以釋放熱能的方式退激,釋放的熱能使樣品和周圍介質按光的
調製頻率產生周期性加熱,從而導致介質產生周期性
壓力波動,這種壓力波動可用靈敏的微音器或壓電陶瓷傳聲器檢測,並通過放大得到光聲信號,這就是
光聲效應。若入射單色光波長可變,則可測到隨波長而變的光聲信號圖譜,這就是光聲光譜。若入射光是聚焦而成的細束光並按
樣品的
x-
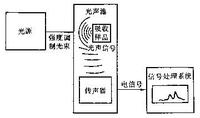
y軸掃描方式移動,則能記錄到光聲信號隨樣品位置的變化,這就是光聲成像技術。光聲光譜的設備及其原理如圖所示。
入射光為強度經過調製的單色光,光強度調製可用切光器。光聲池是一封閉容器,內放樣品和
傳聲器。圖中所示的是固體樣品,樣品周圍充以不吸收
光輻射的氣體介質,如空氣。若是液體或氣體樣品,則用樣品充滿光聲池。傳聲器應很靈敏,對於氣體樣品,電容型
駐極體傳聲器比較適宜,它配以電子檢測系統可測10
-6℃的
溫升或10
-9J/(cm
3·s)的熱量輸入。對於液體和固體樣品,最好採用與樣品緊密接觸的壓電陶瓷檢測器。
 光譜學
光譜學由於
光聲光譜測量的是樣品吸收光能的大小,因而
反射光、
散射光等對測量干擾很小,故光聲光譜適於測量高散射樣品、不透光樣品、吸收光強與
入射光強比值很小的弱吸收樣品和低濃度樣品等,而且樣品無論是晶體、
粉末、
膠體等均可測量,這是普通光譜做不到的。光聲效應與調製頻率有關,改變調製頻率可獲得樣品表面不同深度的信息,所以它是提供表面不同深度結構信息的無損探測方法。
光聲光譜學是光譜技術與
量熱技術結合的產物,是20世紀70年代初發展起來的檢測物質和研究物質性能的新方法。光聲技術在不斷發展,已出現適用於氣體分析的二氧化碳雷射光源紅外光聲光譜儀,適用於固體和液體分析的氙燈紫外-可見光聲光譜儀,以及傅立葉變換光聲光譜儀。光熱偏轉
光譜法、光聲拉曼光譜法、光聲顯微鏡、雷射
熱透鏡法及熱波成像技術都在迅速發展。
光聲光譜技術在物理、化學、生物學、醫學、地質學和材料科學等方面得到廣泛套用。
分類
按物質和光的作用方式分,可分為以下三類:
①發射光譜學
利用原子或分子的
發射光譜進行研究。每種原子和分子都有特定的能級結構和光譜系列,通過對發射光譜的研究可得到關於原子和
分子能級結構的許多知識、測定各種重要
常數以及進行化學元素的定性和
定量分析等。
 光譜學
光譜學②吸收光譜學
分子或原子團在各個
波段均有特徵吸收,主要表現為分子光譜所特有的帶狀吸收譜(見光譜)。廣泛被採用的紅外吸收光譜是由分子的同一電子態內不同振動和轉動
能級間的躍遷產生。
紅外吸收光譜主要用來研究分子的能級結構和分子結構,或進行分子的定性和定量分析等。對吸收光譜和
發射光譜的研究常互為補充。
③拉曼光譜學
在
拉曼散射中,拉曼譜線起源於
散射物質分子的振動和轉動,反映了分子的內部結構和運動,通過拉曼光譜可對化合物進行定性和定量分析、測定分子的振動和轉動頻率及有關常數、了解分子內部或分子間的作用力、推斷分子結構的對稱性和幾何形狀等。拉曼光譜的套用範圍遍及物理學、化學、生物學的許多領域。新型光源雷射的套用有力地推動了拉曼光譜學的發展。
按光源的不同分為,可分為以下兩類:
①雷射光譜學
以雷射為光源的光譜學分支。雷射的
譜線寬度窄、強度高和
方向性好等獨特優點給光譜學帶來了全新的面貌,它不僅具有極高的
光譜解析度和探測靈敏度,而且還開拓了包括
非線性效應和相干拉曼光譜學等在內的許多新領域。
②非雷射光譜學
綜述
研究消除譜線都卜勒增寬的光譜學分支。這裡只涉及非線性領域。提高光譜學的解析度一直是光譜學家努力解決的課題之一。早期
原子光譜的研究工作受到光譜儀的分辨本領的限制,使用了
邁克耳孫干涉儀及
法布里-珀羅干涉儀等靈敏儀器後,便有效地提高了測量光波波長的精密度。但是,對於很靠近的光譜線仍是分辨不開的,例如
氫原子光譜中的巴耳末線的成分。這並不是因為干涉儀的性能不夠完善,而是因為
譜線不夠細銳。譜線的寬度掩蓋了它的細緻結構。
譜線增寬的一部分原因是自然寬度的增加,即使在最佳的觀測條件下,光譜線也不是絕對單色的。其原因是原子的穩態並不是真正的穩態,原子被激發後,會在一定的時間內
輻射能量,也就是說,處於激發態的原子總是要衰變的。激發態的這種有限壽命增大了譜線的自然寬度。
譜線的自然寬度給光譜學的分辨設定了一個限度。但是一直到
雷射器在光譜研究中得到套用之前,幾乎無法達到這個限度,其原因是在氣體樣品中,譜線在更大的程度上為
都卜勒效應所增寬,尋常的光譜學技術無法有效地消除譜線的
都卜勒增寬,因而也就難於提高光譜學的解析度了。
自1970年以來,
雷射光譜學技術得到了很快的發展,這種技術的成效之一是顯著地提高了光譜學的解析度,提高了幾個數量級。雷射光譜學方法能夠有效地消除譜線的都卜勒增寬。這些方法主要是飽和光譜學、偏振光譜學及雙
光子光譜學。
飽和光譜學
依據雷射的兩種主要性質:窄的譜線寬度和高的強度。所使用的雷射器多是連續波調頻雷射器,特別是
染料雷射器。在強雷射
光束中,氣體
原子吸收光子的
速率超過了原子返回原始能級的速率,因而能夠使吸收給定頻率的光子的原子數目有所減少。這就是說,雷射光束在道路上“掃除了”吸收這種頻率的原子。當以相同頻率的另一光束沿著同一道路通過氣體樣品時,就會發現氣體原子對這種頻率的
光的吸收減少了。實際上,利用這種效應進行高分辨光譜學的研究時,是把調頻雷射器的光束分裂成一個強的飽和光束和一個弱的測試光束。所謂飽和光束,粗略地說,就是能夠激發大數目的原子,使原子的激發呈現飽和狀態。這兩條光束沿著相同的路程通過氣體原子樣品,但它們的傳播方向相反。當雷射器的輸出頻率進行掃描並且正好調到原子能級躍遷的頻率時,強的飽和光束便為一組特定的原子所吸收,這些原子在光束方向的速度分量為零。而在光束方向有速度分量的原子,由於都卜勒效應,便不會吸收飽和光束中的光子。飽和光束就使得選定的態上的原子數目減少,因而在測試光束通過原子樣品時,相應地經受到了小的吸收。這種吸收的
頻率範圍由於沒有都卜勒效應而很窄。如果雷射光束的頻率稍稍偏離於
原子躍遷的頻率,則兩個光束便分別地和不同的原子發生相互作用,而不是像光束的頻率恰好為原子躍遷頻率時,兩個光束和同一原子發生相互作用那樣。因此,飽和光束對於測試光束的吸收便不起任何作用。由此可見,飽和光譜技術給出的測試光束信號的寬度很窄,幾乎接近
譜線的自然寬度。
飽和光譜學技術是消除譜線的
都卜勒增寬的有效方法之一,它的用途是很廣的。例子之一是用來研究氫原子光譜的巴耳末α線的
精細結構,研究的結果比以前的精度高得多。此外,在
吸收光譜中首次觀測到了2S┩與2P┩
能級的
蘭姆移位。氫原子光譜的精細結構的精確數據提高了里德伯常數的精度。根據這種研究所確定的里德伯常數
R=(109737.311±0.012)cm,這比以前的精度提高了近10倍。
偏振光譜學
消除都卜勒效應的另一種方法是偏振光譜學技術。這種技術的特點是,測量
光的偏振的微小變化比測量強度的變化要容易得多,因而測量的靈敏度可以明顯地提高。如同在飽和光譜學中那樣,從雷射器出射的
光束也分為兩束,其中一個比另一個要強得多,並且也是以相反方向通過所研究的樣品的。但是,在偏振光譜學中,弱的測試光束是線偏振的並且通過放在交叉偏振器之間的氣體樣品。如果測試光束在通過樣品時不改變它的偏振情況,是不會到達探測器的。但是飽和光束卻能引起這種改變。因為當它首先通過
四分之一波片時,它就變為
圓偏振光了。圓偏振光的
電場方向是轉動的,或是順時針轉動或是逆時針轉動。原子吸收圓偏振光的幾率依賴於原子的角動量的取向。初始原子的取向是無規的,但當某些原子的取向能夠吸收一種圓偏振光後,飽和
光束便使得這些原子所處的原子能級變空了,而具有相反角動量取向的原子相對變多了。當線偏振的測試光束通過氣體的同一區域時,取向的原子便會改變測試光束的傳播。這個原因是容易理解的。
線偏振光可以看作是強度相等的兩種圓偏振光的疊加,一種圓偏振光的電場沿著
順時針方向轉動,另一種圓偏振光的電場沿著逆時針方向轉動。當測試光束通過氣體時,它碰到的原子會過多地吸收一種圓偏振的光,因為這些原子相對的數目是多的。其結果是一種圓偏振光的強度有所減弱,而另一種則相對地變強。因此,從氣體樣品中出來的測試光束不再是線偏振的,而變為
橢圓偏振光了。這樣,測試光束就有了一個分量能夠通過交叉的偏振器。但是,所有這些情況的發生必須是飽和光束與測試光束作用於相同原子上,即無
都卜勒移位的原子上。在這方面偏振光譜學同飽和光譜學是一樣的,事實上,偏振光譜學是從飽和光譜學中派生出來的。這種光譜學技術的最大特點是基本上沒有噪聲,利用這種技術可以得到更為精密的能級結構知識,例如,測量結果把里德伯常數值的精度提高了三倍,而使之成為最精確的已知基本常數。
雙光子光譜學
也是消除光譜線都卜勒增寬的一種好方法。這種技術於1974年首先見諸報導。在這種技術中,一束光由反射鏡沿著原路線反射回去,從而它們沿著相同的光軸向相反方向傳播,疊加後成為
駐波。氣體樣品便放置在駐波場中。如果把雷射光束的頻率調到所選定的原子躍遷頻率的一半時,在一定的條件下,同光束髮生相互作用的每一個原子會同時地從兩個相反方向傳播的光束中各吸收一個光子。
構想在駐波場中沿著光軸方向運動著的一個原子在吸收從相反方向來的兩個光子時,光子之一的
都卜勒移位是朝著紫光方向的,也就是說具有較高的頻率,而另一個光子的都卜勒移位則是朝著紅光方向的,移位的大小同前一個光子的相等。所以,兩個被吸收的光子的總能量為常數,而不管原子的
運動速度如何。因此,
雙光子吸收便抵消了原子運動的都卜勒效應,原子吸收的光頻率之和恰好為原子躍遷頻率。如果雷射器的輸出頻率稍稍偏離於原子躍遷頻率的一半時,原子便不會吸收兩個相反方向的光子。因此,消除譜線
都卜勒增寬的效果是不佳的。即只有當雷射頻率同原子躍遷頻率相匹配時,才能有效地消除都卜勒增寬。
在雙光子吸收光譜學中,所有同雷射光束髮生相互作用的原子都能對無都卜勒效應的信號作出貢獻,而不僅限於垂直光軸方向運動的原子,因此無都卜勒效應的信號是很強的。這同飽和光譜學和偏振光譜學不同。在這兩種光譜中,沒有都卜勒效應的原子是有選擇的,原子的運動要垂直於光軸;而在
雙光子吸收光譜學中,凡是同光束髮生相互作用的原子都可消除其都卜勒效應。
套用領域
高分辨光譜學技術廣泛地套用於原子和分子的能級結構的研究中。直到現在,所得到的資料都屬於驗證理論的預言。但是20世紀物理學中的一些重大變化許多是由於理論和觀測之間微小差別的發現而引起的,高分辨光譜學可能在這方面作出貢獻來。
 光譜學
光譜學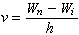 光譜學
光譜學 光譜學
光譜學 光譜學
光譜學 光譜學
光譜學 光譜學
光譜學 光譜學
光譜學 光譜學
光譜學 光譜學
光譜學 光譜學
光譜學
 光譜學
光譜學