瑞利散射定律 散射光 的波長與
入射光 相同,而其強度與波長
λ 4 成反比的散射,稱
瑞利散射 定律,由
瑞利 於1871年提出。此定律成立的條件是散射微粒的
線度 小于波長。若入射光為
自然光 ,不同方向散射光的強度正比於1+
cos 2 θ ,
θ 為散射光與入射光間的夾角,稱
散射角 。
θ =0或π時散射光仍為自然光;
θ =π/2時散射光為
線偏振光 ;在其他方向上則為
部分偏振光 。根據瑞利散射定律可解釋天空的蔚藍色和夕陽的橙紅色。
當散射微粒的線度大于波長時,瑞利散射定律不再成立,
散射光強度 與
微粒 的大小和形狀有複雜的關係。G.米和P.
德拜 分別於1908年和1909年以球形粒子為模型詳細計算3對
電磁波 的散射。米氏散射理論表明,當球形粒子的半徑
a <0.3
λ /-2π時散射
光強 遵守瑞利定律,
a 較大時散射光強與波長的關係不再明顯。用白光照射由大顆粒組成的物質時(如天空的雲層等),散射光仍為白色。
氣體液化 時,在
臨界狀態 附近由密度漲落引起的不均勻區域的線度比波長要大,所產生的強烈散射使原來透明的物質變混濁,稱為
臨界乳光 。
光的散射 拉曼散射 入射光與介質的
分子運動 間相互作用而引起的頻率發生改變的散射。1928年C.拉曼在液體和氣體中觀察到散射光頻率發生改變的現象,稱
拉曼效應 或
拉曼散射 。
喇曼散射 拉曼散射遵守如下規律:
散射光 中在原始入射譜線(頻率為
ω 0 )兩側對稱地伴有頻率為
ω 0 ±
ω i (
i =1,2,3,…)的一組
譜線 ,長波一側的譜線稱紅伴線或
斯托克斯線 ,短波一側的譜線稱紫伴線或
反斯托克斯線 ,統稱拉曼譜線;頻率差
ω i 與入射光頻率
ω 0 無關,僅由散射物質的性質決定。
每種物質都有自己特有的拉曼譜線,常與物質的紅外吸收譜相吻合。在經典理論的解釋中,介質分子以
固有頻率 ω i 振動,與頻率為
ω 0 的入射光耦合後產生
ω 0 、
ω 0 -
ω i 和
ω 0 +
ω i 三種頻率的振動,頻率為
ω 0 的振動輻射瑞利散射光,後兩種頻率對應斯托克斯線和反斯托克斯線。
拉曼散射的詮釋需用
量子力學 ,不僅可解釋散射光的
頻移 ,還能解決諸如強度和
偏振 等問題。
按
量子力學 ,晶體中
原子 的固有振動能量是
量子化 的,所有原子振動形成的
格波 也是量子化的,稱為
聲子 。拉曼散射和布里淵散射都是入射光子與聲子的
非彈性碰撞 結果。
晶格振動 分頻率較高的光學支和頻率較低的聲學支,前者參與的散射是
拉曼散射 ,後者參與的散射是
布里淵散射 。固體中的各種缺陷、雜質等只要能引起
極化率 變化的
元激發 均能產生光的散射過程,稱廣義的拉曼散射。按習慣頻移波數在50—1,000/厘米間為拉曼散射,在0.1—2/厘米間是布里淵散射。
米氏散射 I(λ) scattering∝I(λ)incident/λ
米氏發表了任何尺寸均勻球形粒子散射問題的嚴格解,具有極大的實用價值,可以研究霧、雲、日冕、膠體和金屬懸浮液的散射等。
當大氣中粒子的直徑與輻射的波長相當時發生的散射稱為米氏散射。
這種散射主要由大氣中的微粒,如煙、塵埃、小水滴及氣溶膠等引起。米氏散射的輻射強度與波長的二次方成反比,散射在光線向前的方向比向後的方向更強,方向性比較明顯。如雲霧的粒子大小與紅外線(0.7615um)的波長接近,所以雲霧對紅外線的輻射主要是米氏散射。是故,多雲潮濕的天氣對米氏散射的影響較大
套用 散射與通信技術關係也很密切,如利用對流層、電離層以及流星余跡的散射可對上百乃至幾百公里距離的定點進行微波或超短波通信,是跨越不能設中繼站的地段進行通信的有力措施。此外,微波特別是毫米波穿越雨雲和雨幕時,水滴乃至分子的散射與吸收所引起的衰減是不能忽視的。
對流層中隨時存在著尺度不同(約10~100m)的湍流區。湍流區內與周圍介質的折射率有10-6數量級的差別。這些湍流區如同浸在均勻大氣中的介質塊,在投射被照射下,其極化電流的輻射場即是散射場,團塊極化電流的相位沿著投射波的傳播方向逐漸落後。類似行波天線的原理,其前向散射強度遠大於背向散射。利用這種前向散射可以進行遠距離通信。有效的散射區是收、發天線主波瓣端部相交的區域,見圖。由於團塊的運動、生滅和分布都是隨機的,因而接收信號的幅度和相位也都是隨機起伏的。由於團塊內外折射指數相差甚微,必須使用較高的頻率(常用微波)和相當大的發射功率,才能引起可觀的極化電流。收、發天線也必須有較高的增益。
在電離層中也經常存在著電子濃度與周圍有差異的團塊。由於頻率越高電漿的折射指數越接近於真空,所以利用電離層的不均勻性進行散射通信時只能用米波,而且信號頻帶受到限制。
太陽系大量微粒和流星以12~-72km/s的相對速度與地球相遇時,大多數情形因灼熱而氣化,飛出的原子與大氣分子碰撞而引起電離,選就是流星的電離余跡,它是細長的電漿柱。肉眼能觀察到高度約100km的流星,其餘跡上每米長有1014個以上的自由電子,能在1秒乃至幾分鐘時間內散射米波,在高空風作用下先變形而後散失。估計每一晝夜約有108個這種流星進入大氣,所以這種電離余跡是經常存在的,只是要在發現余跡出現後立即進行斷續通信。其散射的方向性較強,與電離層不均性散射相比,同樣的發射功率下,通信容量增大至10倍或10倍以上。
由於衛星通信的使用,散射通信的必要性已很小,但衛星數量加多必終致發生信道擁擠;空間武器的發展使通信衛星在戰爭中難免被破壞,散射通信或將再度受重視。
對衛星通信和直接廣播影響最明顯的是散射衰減。水珠、雪片乃至大氣分子在電磁波照射下,其極化電流的輻射把照射波的能流轉化為散射能流和質點的內能,因而使照射波受到衰減。在厘米波段,每一水滴如同一個電偶極子。雨滴散射的散射衰減隨頻率提高而加大。在毫米波段則進入散射的諧振區。散射衰減隨頻率增大較快,例如每小時12.5mm的降水中,每公里的衰減分貝數,λ=3cm時約為0.285,λ=1cm時約為2.73,λ=6mm時約為4.72,而λ=3mm時則約為6.72。水蒸汽和氧分子對於毫米波的某些頻率也有強烈的衰減:水汽對於λ=1.35cm的波約有2dB/km的衰減,氧對於λ=5mm和2.5mm的波衰減分別達到3.4和14dB/km。因此對於毫米波通信和廣播必須選用衰減峰之間的頻率,以避免過大的衰減;在計算發射功率時,必須留出足夠的餘量以彌補傳播途徑中的衰減。
 光的散射
光的散射
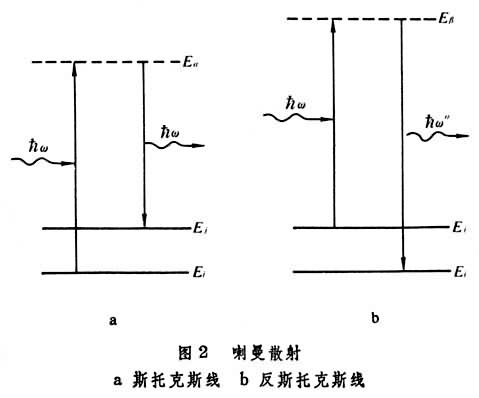 喇曼散射
喇曼散射