基本介紹
- 中文名:傳遞函式矩陣
- 外文名:transfer function matrix
- 定義:線性定常控制系統輸入向量對狀態向量、輸入向量對輸出向量傳遞關係的矩陣
簡單系統


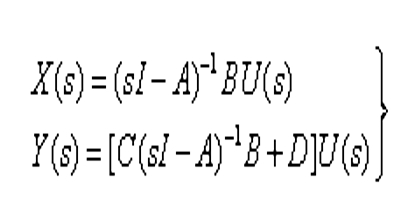
複雜系統
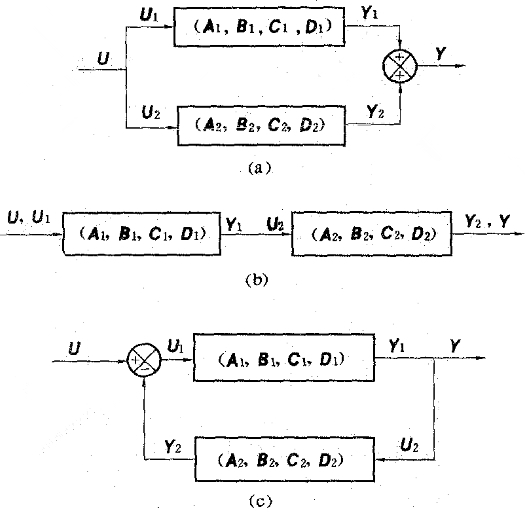



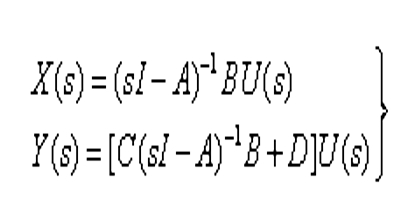

傳遞函式矩陣(transfer function matrix)表示線性定常控制系統輸入向量對狀態向量、輸入向量對輸出向量傳遞關係的矩陣。用於多輸入多輸出控制系統的分析研究。簡單系統一控制系統的狀態空間表達式如下簡寫為(...
狀態傳遞函式矩陣state transfer fuation matrix設有一個系統,共有m個輸入量和m個輸出量,將輸入量看作為向量的各分量,這向量稱之為輸人向量;;‘個輸出量看作是輸出向量的各分量聯繫輸出向量拉氏變換和輸人向量拉氏變換的矩陣,稱...
2D(離散)傳遞函式矩陣(2D (discrete ) transferfunction matrix) 2D系統的一種頻域描述.它是由各種2D線性常係數離散狀態空間模型(或系統輸人及輸出向量)通過二維Z變換得到的系統輸人和輸出關係Y(Z‑Z2)=G(Z‑ZZ)U(Z‑Zz)中...
混合矩陣是可以根據需求將任意信號源定向的切換輸出至任意目標終端的專業設備。背景介紹 1、線性無卷積混外,本文將文獻5的方法推廣到卷積混合信號的分合模型中傳遞函式矩陣(又稱為混合矩陣)為常數矩離,最後給出了語言信號分離的數值模擬...
對於多變數系統,輸入輸出關係的複數域表達式具有矩陣的形式,稱為傳遞函式矩陣,它的每一個元對應地是相應輸入和輸出間的傳遞函式。引入傳遞函式,便有可能採用代數的方法或圖解分析的方法來簡化系統特性的確定和簡化控制系統的分析與綜合。
2.5電機傳遞函式矩陣 2.6小值振盪問題和局部線性化 2.7電機方程中的非線性問題 第三章 電機分析中常用的矩陣變換 3.1線性空間和線性變換 3.2線性變換的意義和目的 3.3連線矩陣 3.4變換的一般約束――恆功率變換 3.5變換的廣義...
並矢矩陣 並矢矩陣(dyadic matrix)非奇異多項式矩陣的一種特殊表示形式。套用 當 其中A。和A,為實常數矩陣,A。非奇異,則GCs為並矢矩陣.如果被控制對象的傳遞函式矩陣是並矢矩陣,則可用並矢展開方法為它設計控制系統.
系統矩陣=一 系統矩陣的轉置,輸入矩陣= 輸出矩陣的轉置,輸出矩陣= 輸入矩陣的轉置。性質 若系統 和系統 互為對偶,且系統 的傳遞函式矩陣為 ,系統 的傳遞函式矩陣為 ,則有 也就是說,互為對偶的系統其傳遞函式陣是互為轉置的。
為了獲得馬爾可夫參數的估計,需要先辨識傳遞函式陣G(z),然後把G(z)展成z的矩陣多項式,其相應的係數矩陣就是馬爾可夫參數的估計。辨識馬爾可夫參數的目的在於建立最小實現的狀態方程,著名的方法之一是何-卡爾曼方法,可表述為:給定{Ji,...
第4章 傳遞函式矩陣 4.1 傳遞函式矩陣的定義 4.2 由狀態空間表達式求傳遞函式矩陣 習題 第5章 基於狀態空間分析法的系統分析 5.1 系統動態特性分析 5.1.1 線性定常系統狀態方程的解 5.1.2 線性時變系統狀態方程...
2.1.2 閉環傳遞函式矩陣與回差矩陣的關係 2.1.3 閉環特徵多項式與開環特徵多項式的關係 2.1.4 關於對象非方時的處理 2.2 多變數控制系統的性能指標 2.2.1 穩定性 2.2.2 多變數系統的交連 2.2.3 魯棒性與故障穩定性 2...
1.2 系統的傳遞函式描述法 1.2.1 單輸入-單輸出系統的傳遞函式描述 1.2.2 系統的傳遞函式矩陣 1.2.3 傳遞函式描述的局限性 1.3 系統的狀態空間描述法 1.3.1 狀態與狀態空間的基本概念 1.3.2 系統的狀態空間描述 1.3.3...
對於線性定常系統,可以把控制向量u(t)視為向量r(t)及x(t)的線性函式,即:u(t)=r(t)-Kx(t)。將上式代入被控控系統的狀態方程:dX(t)/dt=(A-BK)X(t)+Br(t),從而狀態反饋系統的傳遞函式矩陣為:系統在未實行狀態...
9.5 由狀態空間表達式求傳遞函式矩陣 9.5.1傳遞函式矩陣的概念 9.5.2 由狀態空間表達式求傳遞函式矩陣 9.6 離散系統的狀態空間表達式 9.7 線性定常連續系統狀態方程的解 9.7.1 齊次狀態方程的解 9.7.2 狀態轉移矩陣的性質 9...
主要內容包括系統的數學描述、線性系統的運動分析、線性系統的能控性和能觀測性、傳遞函式矩陣的狀態空間實現、系統運動的穩定性、線性系統的狀態反饋與狀態觀測器等。《線性系統理論》是為本科生“現代控制理論”課程編寫的教材,內容豐富,...
(5)正則系統的傳遞函式矩陣為真有理分式矩陣,而線性奇異系統的傳遞函式矩陣不僅通常含有真有理分式矩陣,還含有指數大於1的多項式矩陣。(6)在系統結構參數擾動下,正則系統可以有系統的結構穩定性,而線性奇異系統則通常不再具有結構穩定...
狀態空間的實現(realization of state space)是線性系統頻域描述到時域描述的轉換,它是將傳遞函式矩陣用狀態空間形式描述出來。其中,階數最低的狀態空間描述稱為最小實現,給定線性定常系統Σ(A,B,C),易得其傳遞函式矩陣.反過來,任...
全書共8章,主要內容包括系統的傳遞函式矩陣描述、矩陣分式描述、狀態空間描述和多項式矩陣描述及其相互聯繫,系統運動的定量分析和系統結構性質(能控性、能觀測性、穩定性)的定性分析,傳遞函式矩陣和多項式矩陣描述的實現,多變數反饋控制...
第2章介紹線性系統的狀態空間模型,主要內容包括狀態空間模型的建立、線性系統的標準型、線性系統的傳遞函式矩陣等。第3章介紹線性系統的運動分析,主要內容包括齊次狀態方程求解、非齊次狀態方程求解、線性時變系統的運動解,以及離散時間系統...
根據控制系統開環傳遞函式矩陣的特徵軌跡包圍複數平面上一l+j點的周數,可以判斷閉環系統的穩定性(參見“多變數系統的奈奎斯特穩定性判據”).當m=1,特徵軌跡就退化為標量函式GCs)的奈奎斯特圖象。
對於單變數系統,傳遞函式是以複數變數為自變數的一個標量函式;對於多變數系統,輸入輸出關係的複數域表達式具有矩陣的形式,稱為傳遞函式矩陣,它的每一個元對應地是相應輸入和輸出間的傳遞函式。引入傳遞函式,便有可能採用代數的方法或...
2.7由狀態空間描述導出傳遞函式矩陣 2.7.1傳遞函式矩陣 2.7.2G(s)基於(A,B,C,D)的表達式 2.7.3G(s)的實用計算關係式 2.8線性系統在坐標變換下的特性 2.8.1坐標變換的幾何含義和代數表征 2.8.2線性時不變系統在坐標...
相關對於線性定常系統,系統的超穩定性與其傳遞函式矩陣的正實性之間有著密切關係。澳大利亞學者B.D.O.安德森在1968年證明,在滿足輸入輸出乘積積分值的限定情況下,系統的超穩定性等價於系統傳遞函式矩陣的正實性,系統的超漸近穩定性...
如果存在兩矩陣K及H,使得在控制u=Ka-Hz 作用下,閉環系統 的傳遞函式陣為非奇異對角方陣,則稱系統藝的解禍問題有解(簡稱能解藕).而(K,H)稱為該問題的解.此問題是由摩根(Morgan , B. S.)於1964年提出的,因此也稱為摩根...
對於輸出和輸入變數個數相同的系統,如果引入適當的控制規律,使控制系統的傳遞函式矩陣為非奇異對角矩陣,就稱系統實現了完全解耦。使多變數系統實現完全解耦的控制器,既可採用狀態反饋結合輸入變換的形式,也可採用輸出反饋結合補償裝置的...
3.1 傳遞函式矩陣描述 3.2 矩陣分式描述 3.3 多項式矩陣描述 3.4 各種數學描述方法的互換 第一章習題 第二章 線性系統的動態分析 §1 線性系統的時域分析 1.1 典型輸入函式 1.2 階躍回響分析 1.3 典型系統分析 1.4...
系統的許多內部特性都可通過對系統矩陣的分析而得到。例如,T(S)和U(S)的左互質(它們的左乘公因式矩陣的行列式為非零常數)表示系統的能控性,T(S)和V(S)的右互質則表示系統的能觀測性。系統的傳遞函式矩陣 G(S)與系統矩陣間...
1. 如果有理函式 是正實的,那么 。2. 如果有理函式 是嚴格正實的,那么 都是Hurwitz多項式。套用 在波波夫超穩定性理論中,控制系統在滿足輸入輸出乘積積分值的限定情況下,系統的超穩定性等價於系統傳遞函式矩陣的正實性,系統的超...
