基本介紹
- 中文名:狀態反饋控制
- 外文名:state feedback control
- 領域:自動化控制
- 主要特性:可控性、可觀性
- 主要問題:極點配置問題
簡介
原理




主要特性
可控性



可觀性
極點配置









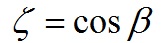
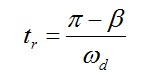
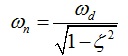
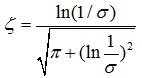
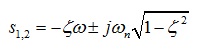
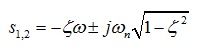
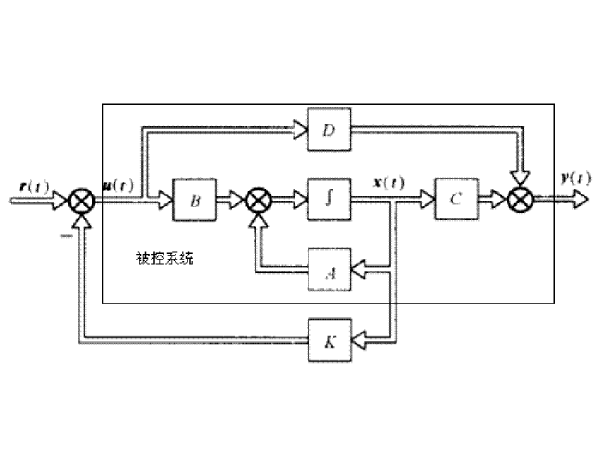

















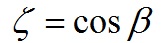
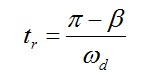
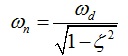
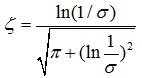
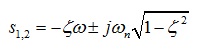
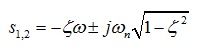
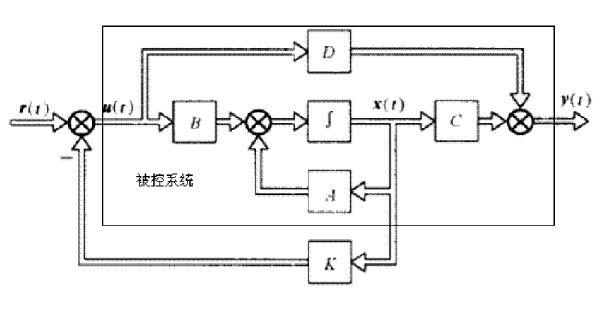
狀態反饋控制是現代控制理論的一種特色。狀態反饋控制是指將系統的每一狀態變數乘以相應的反饋係數, 反饋到輸入端與參考輸入相加,其和作為被控系統的控制信號。一個系統的狀態變數可以展現其整個系統的內部特性而不需要知道系統的內部...
狀態反饋是系統的狀態變數通過比例環節傳送到輸入端去的反饋方式。狀態反饋是體現現代控制理論特色的一種控制方式。狀態變數能夠全面地反映系統的內部特性,因此狀態反饋比傳統的輸出反饋能更有效地改善系統的性能。但是狀態變數往往不能從系統...
全狀態反饋控制(Full State feedback control )是指對於具有二次型性能函式的多維耦合的調節對象,通過求解有關的黎卡提(Riccati)矩陣微分方程來設計最優調節結構的方法。主要特點是能任意配置系統極點位置,從而改善動態回響。反饋控制的...
《離散事件動態系統的狀態反饋控制》是依託西安電子科技大學,由胡奇英擔任項目負責人的青年科學基金項目。中文摘要 研究基於狀態反饋控制的離散事件系統的穩定性問題的馬氏決策過程算法、失誤/О苷鋃霞捌淇刂莆侍猓榷ㄐ雜朧? 失敗、...
輸出反饋 輸出反饋是採用輸出向量構成線性反饋律。在經典控制理論中主要討論這種反饋形式。在不增加補償器的條件下,輸出反饋的效果顯然不如狀態反饋系統好,但輸出反饋在技術實現上的方便性則是其突出優點。工作原理 動態補償器 從系統輸出...
《反饋控制系統導論》是2005年科學出版社出版的圖書,作者是師黎,孔金生。內容簡介 本書系統地介紹了反饋控制系統的理論、方法及其套用。全書共分10章,主要內容包括:反饋控制系統分析、系統建模及其不確定性分析、反饋控制系統穩定性分析...
《自動控制系統(原書第10版)》是2020年機械工業出版社出版的圖書,作者是法里德·高那菲(Farid Golnaraghi),[美] 班傑明,C郭。內容簡介 本書一直被美國及全世界的上百所大學採用。全書內容更加條理化,並且引入了更多的計算機輔助...
《反饋控制系統設計與分析-MATLAB語言套用》是2000年清華大學出版社出版的圖書,作者是薛定宇。內容介紹 MATLAB語言的兩個最顯著特點,即其強大的矩陣運算能力和完美的圖形可視化 功能,使得它成為國際控制界套用最廣的首選計算機工具。現在,...
本書的亮點還在於每個章節都使用了流行軟體MATLAB及其相關的控制系統計算機輔助分析和設計工具箱對基本概念和理論結果進行嚴格的數學運算。章節內容: 狀態空間基本原理 能控性 能觀性 最小實現 穩定性 線性狀態反饋控制系統設計 ...
簡化控制系統的結構另一個典型的例子有最速控制系統、最小能耗控制系統和最省燃料控制系統等。對於這些類型的控制系統,使性能指標最優的控制規律常常難以採用線性狀態反饋實現,而必須採用非線性狀態反饋來實現。在大範圍內改善控制系統的...
具體地,擬開展如下時滯非線性系統控制問題的研究:(1)含狀態延遲下三角系統的全局狀態反饋控制;(2)時滯非線性系統的輸出調節。結題摘要 本項目研究了時滯非線性系統控制中的兩類關鍵問題,即狀態延遲下三角非線性系統的全局狀態反饋...
狀態反饋預測控制系統 近年來, 基於模型的預測控制技術在理論上和套用上都取得了很大的進展, 如動態矩陣控制(DMC) , 廣義預測控制(GPC)和狀態反饋預測控制(SPC)等算法, 都以它獨有的模型預測、反饋校正和滾動最佳化等特點, 越來越受到...
控制系統的基本結構是由受控對象和反饋控制器兩部分構成的閉環系統。在經典理論中習慣於採用輸出反饋,而在現代控制理論中則更多地採用狀態反饋。由於狀態反饋能提高更豐富的狀態信息和可供選擇的自由度,因而使系統容易獲得更為優異的性能。
《幾類增長依賴於不測狀態非線性系統輸出反饋控制設計》是依託山東大學,由劉允剛擔任項目負責人的面上項目。中文摘要 計畫就幾類增長依賴於不可測狀態不確定非線性系統,綜合運用構造性控制器設計、非線性觀測器和Lyapunov穩定性等理論,魯棒...
不過在經典理論中習慣於採用輸出反饋控制,而在現代控制理論中則更多地採用狀態反饋控制。確定系統的動態輸出反饋控制器設計,輸出反饋控制是線性系統控制的主要形式之一,當系統的狀態不可測量時,輸出反饋在一定條件下可實現對系統的控制。
反饋控制是控制理論和控制工程中最重要的一種控制策略。它是用對象的狀態或者輸出來改造控制輸入,使得系統有期望的性能(圖1)。圖1中的Q是非線性運算元時,稱為非線性反饋控制.常用的反饋控制有動態反饋、狀態反饋和輸出反饋三種。亦稱“...
姜偕富等針對帶有輸入時滯的不確定線性時滯系統,基於適當形式的Lyapunov泛函,利用線性矩陣不等式方法討論了時滯相關型魯棒從狀態反饋控制器設計問題,其中不確定性是時變未知的,滿足範數有界條件,其控制器存在的充分條件由線性矩陣不等式的...
單元機組協調控制系統是2020年公布的電力名詞。定義 單元機組的一個主控系統。對動態特性差異較大的鍋爐和汽輪發電機組進行整體負荷平衡控制,使機組儘快回響調度的負荷變化要求,並保證主蒸汽壓力和機爐主要運行參數在允許的範圍內;在一些特定...
SFST自適應補償控制是通過設計自適應狀態反饋控制律,以使系統在執行器故障情況下,其狀態仍能夠跟蹤參考模型的狀態。SFST自適應補償控制研究的關鍵問題在於故障引起的不確定性、系統匹配條件和系統漸近跟蹤性能等的處理。經過10餘年的研究...
TLC方法的設計思想是:首先利用非線性動態逆方法將軌跡跟蹤問題轉化為一個跟蹤誤差調節問題,然後利用線性時變系統PD譜理論設計狀態反饋控制律, 使得該誤差跟蹤系統一致漸近穩定。基本概念 軌跡線性化控制(Trajectory Linearization Control,TLC...
輸出反饋是控制系統設計中兩種主要的反饋策略之一,其意義為將觀測到的輸出取作反饋量以構成反饋律,形成對系統的閉環控制,以達到期望的對系統的性能指標要求。輸出反饋可視為狀態反饋的一個特例。系統套用 單輸入單輸出定常線性系統 對於...
觸發控制系統 接收來自串補控制保護裝置發出的觸發指令,並執行指令使間隙觸發放電的一套控制迴路。主要包括觸發控制箱及其他部件。——引自DL/T1295—2013《串聯補償裝置用火花間隙》
2.1不確定線性切換系統的魯棒狀態反饋鎮定20 2.1.1系統的數學描述與預備知識20 2.1.2魯棒狀態反饋控制器設計21 2.1.3數值算例與仿真22 2.2不確定線性切換系統的魯棒可靠控制24 2.2.1系統的數學描述與預備知識24 2.2.2魯棒...
LQR (linear quadratic regulator)即線性二次型調節器,其對象是現代控制理論中以狀態空間形式給出的線性系統,而目標函式為對象狀態和控制輸入的二次型函式。LQR最優設計是指設計出的狀態反饋控制器 K要使二次型目標函式J 取最小值,...
大多數的關聯時滯系統的研究都集中在簡單的穩定性研究或者狀態反饋控制上。並且,時滯的處理上,時滯相關穩定性的許多結果還難以直接套用到控制器的設計而不犧牲保守性。因此,關聯時滯大系統的分散魯棒控制仍然有其重大的理論與工程意義,它...
在極點配置設計方法中,將反饋全部狀態變數,使得全部閉環極點均設定在各期望的位置上。然而,實際的控制系統中,量測到全部 [4]狀態變數是不可能的,不是全部狀態變數都可以用於反饋。為了實現狀態反饋,估計這些未知的狀態變數是很必要的,這...
控制機制可以是用專門設計的另一稱為監控器的有限自動機來實現的動態邏輯反饋,也可是按系統狀態確定的邏輯反饋.這種監控理論的主要結果,包括用所謂可控子語言概念表達的監控器存在性的充分必要條件;邏輯監控和狀態反饋控制間的關係;等等....
