背景和發展 工業過程最佳化與運行的
自動控制 近年來逐漸成為
控制理論 與工程領域的熱點研究問題。從工程實踐的角度看,工業過程白動化的作用不僅僅要使關鍵過程變數很好地跟蹤設定值的變化,實現工藝上的要求,而且要控制整個生產運行過程中反映產品質量、效率與消耗相關的指標,即運行指標在目標值範圍內,實現過程運行的最佳化控制。
自最佳化控制以工業過程的
經濟效益 為
目標函式 ,在滿足工業過程各種約束條件的情況下,尋找合適的被控變數,用一組固定的常數作為被控變數的設定值,使估燥實際工況處在近似最優操作點上,實際目標函式與最優目標函式的偏差處於可以接受範圍內。實時最佳化(Real time optimization, RTO)將迴路控制與過程運行的最佳化相結合,採用兩層結構,上層線上的實時最佳化經濟
性能指標 ,經計算產生底層控制迴路被控變數的設定值,通過底層控制器作用使被控變數跟蹤
設定值 ,從而儘可能使生產過程運行在經濟最佳化狀態。對於鋼鐵、有色金屬等工業過程,其生產過程往往是動態的.產品牌號的變化、原料成份的波動等因素使生產過程存在各種干擾和不確定動態;另外,生產邊界條件變化、各種運行設備或了系統故障、外部干擾等多種因素常常導致被控系統從一個工作點變到另一個工作點,甚至墓幾享使系統參數發生大範圍跳變.因此,難以採用
RTO 等基於穩態模型的運行最佳化方法。
國外高技術公司針對鋼鐵等工業過程採用預處理手段使原材料成份穩定、生產工況平穩,研發將運行指標轉化為控制迴路設定值的工藝模型或經驗模型,進行開環設定控制.然而我國資源條件和生產條件與國外差別較大,原材料成份波動大,因此狼凶去國外研發的
控制技術 及系統並不適合國情.國內學者針對
我國工業生產過程的上述問題,通常結合具體的工業過程採用基於智慧型技術的運行反饋控制方法。針對熱軋層流冷卻過程將常規控制與基於神經網路、模糊推理的智慧型控制技術相結合,提出了一種混合監控方法,來改善最終產品的性能。提出了基於集成控制的最佳化設定方法,套用於s段步進梁式加熱爐,改善了粱坯的加熱效果。將建模與控制相集成,反饋、預測、前饋相結合,採用案例推理、規則推理、神經網路等智慧型方法,提出了過程最佳化運行的混合智慧型控制方法,套用於赤鐵豎爐,將運行指標控制在目標值範圍內。針對鋁燒結生產線的原料漿製備過程採用機理知識與智慧型技術,提出了基於集成模型和層次推理的設定控制方法。
然而上述自最佳化、
RTO 和智慧型運行反饋控制方法均假設底層過程控制可以跟蹤運行控制給出的設定值,沒有考慮底層跟蹤設定值的動態誤差對雙閉環運行最佳化與控制的影響。結合工業過程中廣泛採用的模型預測控制提出一種更常規的動態運行反饋最優控制策略,並給出了保證系統漸近穩定的充分條件。該方法針對實際流程工業過程的運行特點,提出了運行最佳化反饋控制的兩層結構框架,並採用雙閉環迴路控制方法;建立關於運行指標和底層迴路設定值的無限時域二次型預測控制性能指標;設計了魯棒模型預測控制器以保證運行指標控制最優跟蹤浮選過程,可以動態地給出精礦品位與尾礦品位最佳化設定值,當運行工況受到擾動出現波動時,通過調節作用保證淚只祝判浮選過程運行腿估雅體在目標工況下。
反饋控制 簡介 反饋控制是控制策略的一種特殊方式。反饋控制是控制理論和控制工程中最重要的一種控制策略。它是乎棗付用對象的狀態或者輸出來改造控制輸入,使得系統有期望的性能(圖1)。圖1中的Q是非線性運算元時,稱為非線性反饋控制.常用的反饋控制有動態反饋、狀態反饋和輸出反饋三種。
圖1 亦稱“
閉環控制 ”。一種高精度自控方法。電壓、電流、速度都可閉環。由於能檢測指令速度和實際速度之差而及時反饋,因此能達到控制可控矽觸發角而平滑地控制速度,且平層精度高。
指作為被控的輸出以一定方式返回到作為控制的輸入端,並對輸入端施加控制影響的一種控制關係。在控制論中,閉環通常指輸出端通過“旁鏈”方式回饋到輸入,所謂閉環控制。輸出端回饋到輸入端並參與對輸出端再控制,這才是閉環控制的目的,這種目的是通過反饋來實現的。
區別 開環控制 系統:不將控制的結果反饋回來影響當前控制的系統
舉例:打開燈的開關——按下開關後的一瞬間,控制活動已經結束,燈是否亮起已對按開關的這個活動沒有影響;投籃——籃球出手後就無法再繼續對其控制,無論球進與否,球出手的一瞬間控制活動即結束。
閉環控制系統 :可以將控制的結果反饋回來與希望值比較,並根據它們的誤差調整控制作用的系統
舉例:調節水龍頭——首先在頭腦中對水流有一個期望的流量,水龍頭打開後微糠妹由眼睛觀察現有的流量大小與期望值進行比較,並不斷的用手進行調節形成一個反饋
閉環控制 ;騎腳踏車——同理,不斷的修正行進的方向與速度形成閉環控制。
開環閉環的區別:1、有無反饋;2、是否對當前控制起作用。開環控制一般是在瞬間就完成的控制活動,閉環控制一定會持續一定的時間,可以藉此判斷。
投籃第一次投籃投近了第二次投的時候用力一些,這也是一種反饋但不會對第一次產生影響了,所以是開環控制。
最佳化控制 定義 最佳化
控制 是指在給定的約束條件下,尋求一個控制系統,使給定的被控系統性能指標取得最大或最小值的
控制 。
隨著科學技術的發展,目前智慧型
控制 已開始廣泛套用。這種
控制 將人類的智慧型,例如把適應、學習、探索等能力引入控制系統,使其具有識別、
決策 等功能,從而使自動控制和最佳化控制達到了更高級的階段。
條件 1、要給出系統的性能指標。
2、要給出約束條件。
由於在實際中情況是複雜多變的,進行最佳化
控制 不可能達到十全十美,因此最佳化控制只能是相對的或滿意的控制,而難以做到
最優控制 。
最優控制理論 最優控制理論(optimal control theory),是現代控制理論的一個主要分支,著重於研究使控制系統的性能指標實現最最佳化的基本條件和
綜合方法 。 最優控制理論是研究和解決從一切可能的控制方案中尋找最優解的一門學科。它是現代控制理論的重要組成部分。
最優控制理論所研究的問題可以概括為:對一個受控的動力學系統或運動過程,從一類允許的控制方案中找出一個最優的控制方案,使系統的運動在由某個初始狀態轉移到指定的目標狀態的同時,其性能指標值為最優。這類問題廣泛存在於技術領域或社會問題中。
例如,確定一個最優控制方式使
空間飛行器 由一個軌道轉換到另一軌道過程中燃料消耗最少,選擇一個溫度的調節規律和相應的原料配比使
化工 反應過程的產量最多,制定一項最合理的人口政策使人口發展過程中老化指數、撫養指數和勞動力指數等為最優等,都是一些典型的最優控制問題。最優控制理論是50年代中期在
空間技術 的推動下開始形成和發展起來的。蘇聯學者Л.С.
龐特里亞金 1958年提出的
極大值原理 和美國學者R.貝爾曼1956年提出的動態規劃,對最優控制理論的形成和發展起了重要的作用。
線性系統 在
二次型 性能指標下的最優控制問題則是R.E.卡爾曼在60年代初提出和解決的。
系統集成 集成最佳化控制算法及其實現 網路化系統的集成最佳化控制方法就是將複雜系統的集成最佳化控制方法和網路自動化技術相結合,用來解決網路化複雜系統的最佳化控制問題,使其在難以建模、系統具有網路化和區域化等情況下,獲得滿意的最佳化控制結果。網路化系統集成最佳化
控制 方法的特點是引入了網路迴路,在最佳化算法中引人了一些不確定因素,其最佳化控制更加依賴於網路系統和
網路技術 。網路化系統集成最佳化
控制 的關鍵技術在於動態
系統最佳化 與
參數估計 集成
最佳化方法 的實現和網路
信息傳輸 ,藉助於動態系統集成最佳化控制技術和網路自動化技術可實現網路化系統的集成最佳化控制,可以基於
區域網路 或Intemet實現。
集成最佳化控制的特徵 對一個動態最佳化控制方法,除了給出最佳化算法,還需要對其性能進行分析,只有這樣才能保證
最佳化方法 的實施。網路化系統的集成最佳化
控制 方法的性能包括實時性、最優性、收斂性及其魯棒性等。
1).實時性 在引人網路之前,針對跨區域的複雜系統,其最佳化
控制 的實施是很困難的,即使能夠,其實時性也難以保證。網路化系統集成最佳化
控制 方法由於藉助於計算機
網路技術 來實施集成最佳化控制,可以較好地解決跨區域複雜系統集成最佳化控制的實時性問題。
2).最優性 算法最優性是指在算法收斂的情況下,收斂解是否實際系統的最優解。對於網路化系統集成最佳化
控制 方法,在最優解存在且唯一等假設條件下,若算法收斂,則收斂解滿足最優性必要條件,即所得最佳化解是實際系統的真實最優解。
3).收斂性 網路化系統集成最佳化
控制 方法需要實施,首先要求其最佳化控制算法是收斂的,收斂性就是研究算法收斂的條件,針對不同的算法其收斂性條件有所不同。對於網路化系統的集成最佳化
控制 方法,其最佳化的框架沒有改變,只是引人了網路迴路,利用算法映射及壓縮映射原理,通過分析可以獲得保證最佳化算法收斂的條件。
4).魯棒性 網路化系統集成最佳化
控制 方法的魯棒性問題是指在存在這樣那樣擾動的情況下,最佳化算法保持其收斂性,並收斂到最優解的能力。網路化系統的集成最佳化
控制 方法在不需要實際過程的精確
數學模型 的情況下可以獲得實際系統的真實最優解,對模型的結構和參數具有較強的魯棒性。
網路化系統的集成最佳化
控制 方法是一種基於網路環境下的集成最佳化控制方法,計算機網路的信息的安全問題必然影響到系統集成最佳化控制的實施。因此,對網路化系統集成最佳化
控制 中的
信息安全 問題及其對策進行分析和研究是十分必要的,只有這樣才能保證網路化系統的集成最佳化控制的順利實施。網路化系統集成最佳化
控制 中的
信息安全 問題可以藉助於計算機網路的信息安全對策予以解決。
優越性 網路化系統的集成最佳化
控制 方法為解決區域性複雜系統的最佳化
控制 提供了一種新思路,該方法具有以下優越性:
1)由於網路化系統的集成最佳化
控制 方法本質是採用動態大系統的DISOPE遞階
最佳化方法 ,這樣就使得網路化系統的集成最佳化控制在不需要複雜系統的精確
數學模型 的情況下,就可以獲得實際系統的真實最優解;
2)網路化系統的集成最佳化控制方法為解決跨區域性的複雜系統的最佳化控制提供了一種可靠的實現途徑和形式。同時由於網路自動化技術的發展和網路
信息傳輸 實時性的提高,使得實時地解決區域性的複雜系統的最佳化
控制 成為可能。
主要方法 為了解決最優控制問題,必須建立描述受控運動過程的
運動方程 ,給出
控制變數 的允許取值範圍,指定運動過程的初始狀態和目標狀態,並且規定一個評價運動過程品質優劣的性能指標。通常,性能指標的好壞取決於所選擇的控制
函式 和相應的
運動狀態 。系統的
運動狀態 受到運動方程的約束,而控制
函式 只能在允許的範圍內選取。因此,從
數學 上看,確定最優控制問題可以表述為:在
運動方程 和允許控制範圍的約束下,對以控制
函式 和運動狀態為變數的性能指標函式(稱為
泛函 )求取
極值 (極大值或極小值)。解決最優控制問題的主要方法有
古典變分法 、
極大值原理 和動態規劃。
古典變分法 研究對
泛函 求
極值 的一種
數學方法 。
古典變分法 只能用在
控制變數 的取值範圍不受限制的情況。在許多實際控制問題中,控制
函式 的取值常常受到封閉性的邊界限制,如方向舵只能在兩個極限值範圍內轉動,電動機的
力矩 只能在正負的最大值範圍內產生等。因此,
古典變分法 對於解決許多重要的實際最優控制問題,是無能為力的。
極大值原理 動態規劃 動態規劃是數學規劃的一種,同樣可用於
控制變數 受限制的情況,是一種很適合於在計算機上進行計算的比較有效的方法。
最優控制理論已被套用於最省燃料控制系統、最小能耗控制系統、
線性調節器 等。
最佳化技術 最優控制的實現離不開最最佳化技術,最最佳化技術是研究和解決
最最佳化問題 的一門學科,它研究和解決如何從一切可能的方案中尋找最優的方案。也就是說,最最佳化技術是研究和解決如何將
最最佳化問題 表示為數學模型以及如何根據數學模型儘快求出其最優解這兩大問題。一般而言,用最最佳化方法解決實際工程問題可分為三步進行:
①根據所提出的
最最佳化問題 ,建立最最佳化問題的數學模型,確定變數,列出約束條件和目標函式;
②對所建立的數學模型進行具體分析和研究,選擇合適的最最佳化方法;
③根據最最佳化方法的
算法 列出程式框圖和編寫程式,用計算機求出最優解,並對算法的收斂性、通用性、簡便性、計算效率及
誤差 等作出評價。
求解方法 所謂
最最佳化問題 ,就是尋找一個最優控制方案或最優控制規律,使系統能最優地達到預期的目標。在
最最佳化問題 的數學模型建立後,主要問題是如何通過不同的求解方法解決尋優問題。一般而言,最最佳化方式有離線靜態最佳化方式和線上動態最佳化方式,而
最最佳化問題 的求解方法大致可分為四類:
解析法 這種方法適用於性能指標及約束有明顯解析表達式的情況。其一般步是先用求導方法或變分法求出最優控制的必要條件,得到一組方程或不等式,然後求解這組方程或不等式,得到最優控制的解析解即為所求的最優控制。解析法大致可分為兩大類。第一類,無約束時,採用微分法或變分法。第二類,有約束時,採用極大值原理或動態規劃。
(1)變分法:當控制向量不受約束時,引入
哈密頓函式 ,套用變分法可以導出最優控制的必要條件,即正則方程、控制方程、邊界條件、橫截條件。
(2)極大值原理:在用變分法求解最優控制問題時,是假定控制向量u(O)不受任何限制,即容許控制集合可以看成是整個P維控制空間開集,控制變分u是任意的,同時還要求哈密頓出數H對u連續可微,但在實際工程上,控制變數往往受到一定的限制,這時可以用極大值原理來求解最優控制問題,這種方法其實是由變分法引申而來的,但由於它能套用於控制變數u(t)受邊界限制的情況,並且不要求哈密頓出數H對u連續可微,因此獲得了廣泛的套用。
(3)動態規劃:極大值原理一樣,是處理控制向量限制在一定閉集內的最優控制問題的有效數學方法,它把複雜的最優控制間題變為多級決策過程的遞推函式關係,其基礎和核心時
最優性原理 即在一個多級決策問題中無論初始狀態和初始決策如何,當把其中的任何一級和狀態再作為初始級和初始狀態時,如下的決定對與這一級開始往後的多級決策過程的一部分必定仍然是一個最優決策。因此,利用這一最優性原理必然可把一個多級決策問題化為最優的單級決策問題並且本級決策與本級以前的任何決策無關,只與本級的初始位置和初始決策有關。對於連續系統用
動態規劃法 求最優控制問題時,可以先把連續系統離散化,用有限差分方程近似代替連續方程,然後用離散動態規劃法求解。
數值解法(直接法) 對於
目標函式 較為複雜或無明確的數學表達式或無法用
解析法 求解的
最最佳化問題 ,通常可採用直接法來解決。直接法的基本思想,就是用直接搜尋方法經過一系列的疊代以產生點的序列,使之逐步接近到最優點。直接法常常是根據經驗或實驗而得到的。
性能指標比較複雜或不能用變數顯函式表示時,可以採用
直接搜尋法 ,經過若干次疊代搜尋到最優點,數值計算法可以分為兩大類:
(2)爬山法,又稱多維搜尋法,適用於求解多變數極值問題。主要有坐標輪轉法、步長加速法等。
解析與數值相結合的尋優方法(梯度型法) 是一種解析與數值計算相結合的方法。主要包括兩大類:一種是無約束梯度法,如陡降法、擬牛頓法等。第二類是有約束梯度法,如可行方向法、
梯度投影法 。
網路最最佳化方法 這種方法以網路圖作為數學模型,用
圖論 方法進行搜尋的尋優方法。
反饋控制是控制策略的一種特殊方式。反饋控制是控制理論和控制工程中最重要的一種控制策略。它是用對象的狀態或者輸出來改造控制輸入,使得系統有期望的性能(圖1)。圖1中的Q是非線性運算元時,稱為非線性反饋控制.常用的反饋控制有動態反饋、狀態反饋和輸出反饋三種。
圖1 亦稱“
閉環控制 ”。一種高精度自控方法。電壓、電流、速度都可閉環。由於能檢測指令速度和實際速度之差而及時反饋,因此能達到控制可控矽觸發角而平滑地控制速度,且平層精度高。
指作為被控的輸出以一定方式返回到作為控制的輸入端,並對輸入端施加控制影響的一種控制關係。在控制論中,閉環通常指輸出端通過“旁鏈”方式回饋到輸入,所謂閉環控制。輸出端回饋到輸入端並參與對輸出端再控制,這才是閉環控制的目的,這種目的是通過反饋來實現的。
開環控制 系統:不將控制的結果反饋回來影響當前控制的系統
舉例:打開燈的開關——按下開關後的一瞬間,控制活動已經結束,燈是否亮起已對按開關的這個活動沒有影響;投籃——籃球出手後就無法再繼續對其控制,無論球進與否,球出手的一瞬間控制活動即結束。
閉環控制系統 :可以將控制的結果反饋回來與希望值比較,並根據它們的誤差調整控制作用的系統
舉例:調節水龍頭——首先在頭腦中對水流有一個期望的流量,水龍頭打開後由眼睛觀察現有的流量大小與期望值進行比較,並不斷的用手進行調節形成一個反饋
閉環控制 ;騎腳踏車——同理,不斷的修正行進的方向與速度形成閉環控制。
開環閉環的區別:1、有無反饋;2、是否對當前控制起作用。開環控制一般是在瞬間就完成的控制活動,閉環控制一定會持續一定的時間,可以藉此判斷。
投籃第一次投籃投近了第二次投的時候用力一些,這也是一種反饋但不會對第一次產生影響了,所以是開環控制。
最佳化
控制 是指在給定的約束條件下,尋求一個控制系統,使給定的被控系統性能指標取得最大或最小值的
控制 。
隨著科學技術的發展,目前智慧型
控制 已開始廣泛套用。這種
控制 將人類的智慧型,例如把適應、學習、探索等能力引入控制系統,使其具有識別、
決策 等功能,從而使自動控制和最佳化控制達到了更高級的階段。
1、要給出系統的性能指標。
2、要給出約束條件。
由於在實際中情況是複雜多變的,進行最佳化
控制 不可能達到十全十美,因此最佳化控制只能是相對的或滿意的控制,而難以做到
最優控制 。
最優控制理論(optimal control theory),是現代控制理論的一個主要分支,著重於研究使控制系統的性能指標實現最最佳化的基本條件和
綜合方法 。 最優控制理論是研究和解決從一切可能的控制方案中尋找最優解的一門學科。它是現代控制理論的重要組成部分。
最優控制理論所研究的問題可以概括為:對一個受控的動力學系統或運動過程,從一類允許的控制方案中找出一個最優的控制方案,使系統的運動在由某個初始狀態轉移到指定的目標狀態的同時,其性能指標值為最優。這類問題廣泛存在於技術領域或社會問題中。
例如,確定一個最優控制方式使
空間飛行器 由一個軌道轉換到另一軌道過程中燃料消耗最少,選擇一個溫度的調節規律和相應的原料配比使
化工 反應過程的產量最多,制定一項最合理的人口政策使人口發展過程中老化指數、撫養指數和勞動力指數等為最優等,都是一些典型的最優控制問題。最優控制理論是50年代中期在
空間技術 的推動下開始形成和發展起來的。蘇聯學者Л.С.
龐特里亞金 1958年提出的
極大值原理 和美國學者R.貝爾曼1956年提出的動態規劃,對最優控制理論的形成和發展起了重要的作用。
線性系統 在
二次型 性能指標下的最優控制問題則是R.E.卡爾曼在60年代初提出和解決的。
系統集成 集成最佳化控制算法及其實現 網路化系統的集成最佳化控制方法就是將複雜系統的集成最佳化控制方法和網路自動化技術相結合,用來解決網路化複雜系統的最佳化控制問題,使其在難以建模、系統具有網路化和區域化等情況下,獲得滿意的最佳化控制結果。網路化系統集成最佳化
控制 方法的特點是引入了網路迴路,在最佳化算法中引人了一些不確定因素,其最佳化控制更加依賴於網路系統和
網路技術 。網路化系統集成最佳化
控制 的關鍵技術在於動態
系統最佳化 與
參數估計 集成
最佳化方法 的實現和網路
信息傳輸 ,藉助於動態系統集成最佳化控制技術和網路自動化技術可實現網路化系統的集成最佳化控制,可以基於
區域網路 或Intemet實現。
集成最佳化控制的特徵 對一個動態最佳化控制方法,除了給出最佳化算法,還需要對其性能進行分析,只有這樣才能保證
最佳化方法 的實施。網路化系統的集成最佳化
控制 方法的性能包括實時性、最優性、收斂性及其魯棒性等。
1).實時性 在引人網路之前,針對跨區域的複雜系統,其最佳化
控制 的實施是很困難的,即使能夠,其實時性也難以保證。網路化系統集成最佳化
控制 方法由於藉助於計算機
網路技術 來實施集成最佳化控制,可以較好地解決跨區域複雜系統集成最佳化控制的實時性問題。
2).最優性 算法最優性是指在算法收斂的情況下,收斂解是否實際系統的最優解。對於網路化系統集成最佳化
控制 方法,在最優解存在且唯一等假設條件下,若算法收斂,則收斂解滿足最優性必要條件,即所得最佳化解是實際系統的真實最優解。
3).收斂性 網路化系統集成最佳化
控制 方法需要實施,首先要求其最佳化控制算法是收斂的,收斂性就是研究算法收斂的條件,針對不同的算法其收斂性條件有所不同。對於網路化系統的集成最佳化
控制 方法,其最佳化的框架沒有改變,只是引人了網路迴路,利用算法映射及壓縮映射原理,通過分析可以獲得保證最佳化算法收斂的條件。
4).魯棒性 網路化系統集成最佳化
控制 方法的魯棒性問題是指在存在這樣那樣擾動的情況下,最佳化算法保持其收斂性,並收斂到最優解的能力。網路化系統的集成最佳化
控制 方法在不需要實際過程的精確
數學模型 的情況下可以獲得實際系統的真實最優解,對模型的結構和參數具有較強的魯棒性。
網路化系統的集成最佳化
控制 方法是一種基於網路環境下的集成最佳化控制方法,計算機網路的信息的安全問題必然影響到系統集成最佳化控制的實施。因此,對網路化系統集成最佳化
控制 中的
信息安全 問題及其對策進行分析和研究是十分必要的,只有這樣才能保證網路化系統的集成最佳化控制的順利實施。網路化系統集成最佳化
控制 中的
信息安全 問題可以藉助於計算機網路的信息安全對策予以解決。
優越性 網路化系統的集成最佳化
控制 方法為解決區域性複雜系統的最佳化
控制 提供了一種新思路,該方法具有以下優越性:
1)由於網路化系統的集成最佳化
控制 方法本質是採用動態大系統的DISOPE遞階
最佳化方法 ,這樣就使得網路化系統的集成最佳化控制在不需要複雜系統的精確
數學模型 的情況下,就可以獲得實際系統的真實最優解;
2)網路化系統的集成最佳化控制方法為解決跨區域性的複雜系統的最佳化控制提供了一種可靠的實現途徑和形式。同時由於網路自動化技術的發展和網路
信息傳輸 實時性的提高,使得實時地解決區域性的複雜系統的最佳化
控制 成為可能。
主要方法 為了解決最優控制問題,必須建立描述受控運動過程的
運動方程 ,給出
控制變數 的允許取值範圍,指定運動過程的初始狀態和目標狀態,並且規定一個評價運動過程品質優劣的性能指標。通常,性能指標的好壞取決於所選擇的控制
函式 和相應的
運動狀態 。系統的
運動狀態 受到運動方程的約束,而控制
函式 只能在允許的範圍內選取。因此,從
數學 上看,確定最優控制問題可以表述為:在
運動方程 和允許控制範圍的約束下,對以控制
函式 和運動狀態為變數的性能指標函式(稱為
泛函 )求取
極值 (極大值或極小值)。解決最優控制問題的主要方法有
古典變分法 、
極大值原理 和動態規劃。
古典變分法 研究對
泛函 求
極值 的一種
數學方法 。
古典變分法 只能用在
控制變數 的取值範圍不受限制的情況。在許多實際控制問題中,控制
函式 的取值常常受到封閉性的邊界限制,如方向舵只能在兩個極限值範圍內轉動,電動機的
力矩 只能在正負的最大值範圍內產生等。因此,
古典變分法 對於解決許多重要的實際最優控制問題,是無能為力的。
極大值原理 動態規劃 動態規劃是數學規劃的一種,同樣可用於
控制變數 受限制的情況,是一種很適合於在計算機上進行計算的比較有效的方法。
最優控制理論已被套用於最省燃料控制系統、最小能耗控制系統、
線性調節器 等。
最佳化技術 最優控制的實現離不開最最佳化技術,最最佳化技術是研究和解決
最最佳化問題 的一門學科,它研究和解決如何從一切可能的方案中尋找最優的方案。也就是說,最最佳化技術是研究和解決如何將
最最佳化問題 表示為數學模型以及如何根據數學模型儘快求出其最優解這兩大問題。一般而言,用最最佳化方法解決實際工程問題可分為三步進行:
①根據所提出的
最最佳化問題 ,建立最最佳化問題的數學模型,確定變數,列出約束條件和目標函式;
②對所建立的數學模型進行具體分析和研究,選擇合適的最最佳化方法;
③根據最最佳化方法的
算法 列出程式框圖和編寫程式,用計算機求出最優解,並對算法的收斂性、通用性、簡便性、計算效率及
誤差 等作出評價。
求解方法 所謂
最最佳化問題 ,就是尋找一個最優控制方案或最優控制規律,使系統能最優地達到預期的目標。在
最最佳化問題 的數學模型建立後,主要問題是如何通過不同的求解方法解決尋優問題。一般而言,最最佳化方式有離線靜態最佳化方式和線上動態最佳化方式,而
最最佳化問題 的求解方法大致可分為四類:
解析法 這種方法適用於性能指標及約束有明顯解析表達式的情況。其一般步是先用求導方法或變分法求出最優控制的必要條件,得到一組方程或不等式,然後求解這組方程或不等式,得到最優控制的解析解即為所求的最優控制。解析法大致可分為兩大類。第一類,無約束時,採用微分法或變分法。第二類,有約束時,採用極大值原理或動態規劃。
(1)變分法:當控制向量不受約束時,引入
哈密頓函式 ,套用變分法可以導出最優控制的必要條件,即正則方程、控制方程、邊界條件、橫截條件。
(2)極大值原理:在用變分法求解最優控制問題時,是假定控制向量u(O)不受任何限制,即容許控制集合可以看成是整個P維控制空間開集,控制變分u是任意的,同時還要求哈密頓出數H對u連續可微,但在實際工程上,控制變數往往受到一定的限制,這時可以用極大值原理來求解最優控制問題,這種方法其實是由變分法引申而來的,但由於它能套用於控制變數u(t)受邊界限制的情況,並且不要求哈密頓出數H對u連續可微,因此獲得了廣泛的套用。
(3)動態規劃:極大值原理一樣,是處理控制向量限制在一定閉集內的最優控制問題的有效數學方法,它把複雜的最優控制間題變為多級決策過程的遞推函式關係,其基礎和核心時
最優性原理 即在一個多級決策問題中無論初始狀態和初始決策如何,當把其中的任何一級和狀態再作為初始級和初始狀態時,如下的決定對與這一級開始往後的多級決策過程的一部分必定仍然是一個最優決策。因此,利用這一最優性原理必然可把一個多級決策問題化為最優的單級決策問題並且本級決策與本級以前的任何決策無關,只與本級的初始位置和初始決策有關。對於連續系統用
動態規劃法 求最優控制問題時,可以先把連續系統離散化,用有限差分方程近似代替連續方程,然後用離散動態規劃法求解。
數值解法(直接法) 對於
目標函式 較為複雜或無明確的數學表達式或無法用
解析法 求解的
最最佳化問題 ,通常可採用直接法來解決。直接法的基本思想,就是用直接搜尋方法經過一系列的疊代以產生點的序列,使之逐步接近到最優點。直接法常常是根據經驗或實驗而得到的。
性能指標比較複雜或不能用變數顯函式表示時,可以採用
直接搜尋法 ,經過若干次疊代搜尋到最優點,數值計算法可以分為兩大類:
(2)爬山法,又稱多維搜尋法,適用於求解多變數極值問題。主要有坐標輪轉法、步長加速法等。
解析與數值相結合的尋優方法(梯度型法) 是一種解析與數值計算相結合的方法。主要包括兩大類:一種是無約束梯度法,如陡降法、擬牛頓法等。第二類是有約束梯度法,如可行方向法、
梯度投影法 。
網路最最佳化方法 這種方法以網路圖作為數學模型,用
圖論 方法進行搜尋的尋優方法。
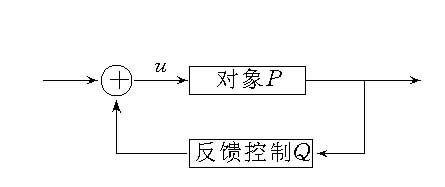 圖1
圖1 圖1
圖1