最優性原理是指“多階段決策過程的最優決策序列具有這樣的性質:不論初始狀態和初始決策如何,對於前面決策所造成的某一狀態而言,其後各階段的決策序列必須構成最優策略”。
基本介紹
- 中文名:最優性原理
- 外文名:optimality principle
- 方法:反證法
- 內容:多階段決策過程的最優決策序列
- 性質:動態規劃的基礎
- 套用學科:數學術語
概念
基本原理


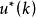
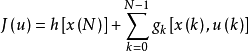
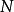
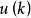
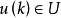
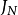

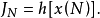
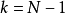
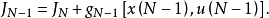
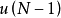

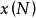
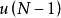

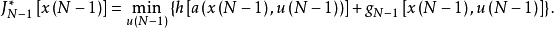



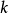
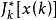
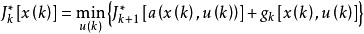
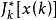
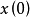
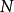

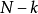
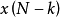
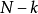


最優性原理是指“多階段決策過程的最優決策序列具有這樣的性質:不論初始狀態和初始決策如何,對於前面決策所造成的某一狀態而言,其後各階段的決策序列必須構成最優策略”。


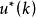
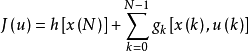
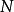
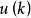
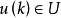
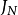

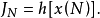
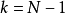
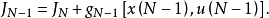
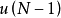

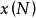
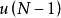

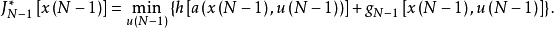



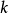
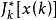
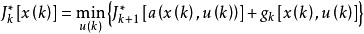
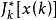
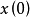
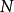

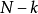
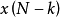
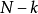


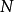
最優性原理是指“多階段決策過程的最優決策序列具有這樣的性質:不論初始狀態和初始決策如何,對於前面決策所造成的某一狀態而言,其後各階段的決策序列必須構成最優...
最最佳化原理也稱最優性原理。指解決多階段決策問題的理論。這個理論是美國的貝爾曼在1956年提出的。它原來的表述是:一個過程的最優策略具有這樣的性質,即無論其初始...
其基礎和核心時最優性原理即在一個多級決策問題中無論初始狀態和初始決策如何,當把其中的任何一級和狀態再作為初始級和初始狀態時,如下的決定對與這一級開始往後...
《最優控制理論與方法》是2002年出版的圖書,作者是荊海英。本書主要介紹了最優控制理論的三種方法,即變分法、最大值原理與動態規劃方法。...
《最最佳化原理與方法》是1992年冶金工業出版社出版的圖書,作者是冶金工業出版社發行部。...
本書含有大量經典的和新近的算法,有比較系統的理論分析,實用性比較強;定理的...第7章最優性條件7.1無約束問題的極值條件7.2約束極值問題的最優性條件...
《錐約束最佳化——最優性理論與增廣Lagrange方法》是2010年1月科學出版社出版的圖書,作者是張立衛。...
極大值原理是20世紀50年代中期蘇聯學者Л.С.龐特里亞金提出的,有關這一原理的主要結果及其嚴格的數學證明,都發表在後來出版的《最優過程的數學理論》一書中。...
對於線性二次型高斯(LQG)隨機過程控制問題,包括它的特例最小方差控制問題,可以套用分離原理把隨機最優控制問題分解成狀態估計問題和確定性最優控制問題,最終能得到...
3.2 Lagrange對偶性3.3 對偶理論的套用第4章 最優性條件4.1 約束最佳化模型4.2 一階最優性條件4.3 廣義Lagrange乘子4.4 Ekeland變分原理...
簡而言之,一個最最佳化策略的子策略總是最優的。一個問題滿足最最佳化原理又稱其具有最優子結構性質。2.無後效性將各階段按照一定的次序排列好之後,對於某個給定的...
動態規劃的理論基礎是最優性原理和嵌入原理 [3] 。最最佳化原理一個最優策略,具有如下性質:不論初始狀態和初始決策(第一步決策)如何,以第一步決策所形成的階段...
(2)極大值原理:在用變分法求解最優控制問題時,是假定控制向量u(O)不受任何限制,即容許控制集合可以看成是整個P維控制空間開集,控制變分u是任意的,同時還...
