基本介紹
- 中文名:系統實現問題
- 外文名:system realization problem
- 所屬學科:數學
- 簡介:系統分析的反問題
基本介紹



相關介紹






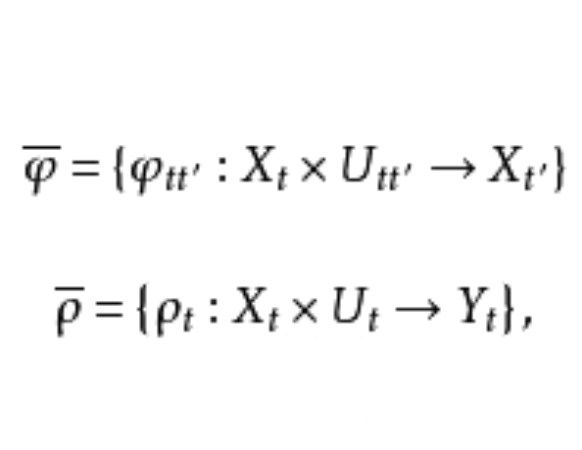









系統實現問題(system realization problem)是系統分析的反問題,指由系統輸入-輸出之間的外部關係求其完整的狀態空間內部描述的問題。基本介紹系統實現問題指由系統輸入-輸出之間的外部關係求其完整的狀態...
《軟體系統實現與分析》是2011年4月1日清華大學出版社出版的圖書,作者是於萬波。內容簡介 《軟體系統實現與分析》以java作為工具講解了4個軟體系統,分別是學生管理信息系統、象棋對弈軟體、部落格系統與網上購物系統。在每個系統的講解過程中...
系統故障是指系統在運行過程中,由於某種原因,以致事務在執行過程中以非正常的方式終止。按故障的部件可將故障分為硬體故障和軟體故障。硬體故障是指故障因硬體系統失效。軟體故障是指程式運行一些非法指令,如特權指令。事務 事務的定義 ...
專家系統技術可以用於工程設計,工藝過程設計,生產調度,故障診斷等。也可以將神經網路和模糊控制技術等先進的計算機智慧型方法套用於產品配方,生產調度等,實現製造過程智慧型化。而人工智慧技術尤其適合於解決特別複雜和不確定的問題。但同樣顯然...
1)電源冗餘:高端伺服器產品普遍採用雙電源系統,這兩個電源是負載均衡的,即在系統工作時它們同時為系統提供電力,當一個電源出現故障時,另一個電源會立即承擔所有的負載。有些伺服器系統實現了直流電源的冗餘,另一些伺服器產品實現了...
系統設計是合理設計、開發和運用系統的思想和方法論,“是將對象看作由多重因素交織構成的一個系統,並以此為基點展開創意”。設計原則 系統設計總的原則是保證系統設計目標的實現,並在此基礎上使技術資源的運用達到最佳。系統設計中,應...
而企業在縱向結構中的位置,就是確定單個企業的供應鏈流程的需求、顧客價值的實現情況,分析企業內流程中存在的問題和根源。(2)供應鏈業務流程:確定在供應鏈系統中哪些核心流程應該連線並集成起來。全球供應鏈論壇將供應鏈中的流程總結為...
B/S體系結構只需維護伺服器,所有的客戶端只是瀏覽器,不需要任何維護和管理,而且只需將伺服器連線專網,即可實現遠程維護、升級和共享。C/S體系結構維護複雜,處理出現的問題以及系統升級困難,系統擴展性不好。P2P體系結構系統內計算機...
此外,中文的WordNet、“同義詞詞林”等也常在開放域問答系統中使用。按支持問答系統產生答案的文檔庫、知識庫,以及實現的技術分類,可分為自然語言的資料庫問答系統、對話式問答系統、閱讀理解系統、基於常用問題集的問答系統、基於知識庫...
(1)系統應用程式維護。套用軟體維護是系統維護的最主要內容。它是指對相應的應用程式及有關文檔進行的修改和完善。系統的業務處理過程是通過應用程式的運行而實現的,一旦程式發生問題或業務發生變化,就必然地引起程式的修改和調整,因此...
計算機的操作系統根據不同的用途分為不同的種類,從功能角度分析,分別有實時系統、批處理系統、分時系統、網路作業系統等。實時系統主要是指系統可以快速的對外部命令進行回響,在對應的時間裡處理問題,協調系統工作。分時系統可以實現用戶...
目前,GO法及其改進算法已廣泛套用於各類型系統的可靠性分析中,用GO法代替計算複雜組合的可靠性聯合機率,降低了計算機編程實現的難度。將最短路徑集與GO法相結合,使得GO法利用計算機編程實現的難度進一步降低。將GO法套用於供應鏈系統的...
系統介紹 DCS通常採用分級遞階結構,每一級由若干子系統組成,每一個子系統實現若干特定的有限目標,形成金字塔結構。可靠性是DCS發展的生命,要保證DCS的高可靠性主要有三種措施:一是廣泛套用高可靠性的硬體設備和生產工藝;二是廣泛採用...
可能性來看,過程控制是朝綜合化、智慧型化方向發展,即計算機集成製造系統(CIMS):以智慧型控制理論為基礎,以計算機及網路為主要手段,對企業的經營、計畫、調度、管理和控制全面綜合,實現從原料進庫到產品出廠的自動化、整個生產系統信息管理的...
建立企業內部信息交流、業務交流、知識交流的快速通道,以共享信息資源,強化部門業務管理,加強各業務部門之間的交流,實現公司信息的快速上傳下達,促進業務協同,提高工作效率,為各級領導及業務人員提供輔助辦公和決策服務。常見問題 在當前...
系統分析階段回答了新系統“做什麼”的問題,而系統設計階段的任務就是回答“怎么做”的問題,即根據系統分析說明書中規定的功能要求,考慮實際條件,具體設計實現邏輯模型的技術方案,也即設計新系統的物理模型。所以這個階段又稱為物理設計...
隨著科學技術的發展,日益廣泛採用的微電子技術和電氣化的逐步實現,形成了複雜的電磁環境。不斷研究和解決電磁環境中設備之間以及系統間相互關係的問題,促進了電磁兼容技術的迅速發展。電磁兼容設計要求 在進行電磁兼容設計時要求:①明確...
存儲器是具有記憶功能的半導體電路,它的作用是存放系統程式、用戶程式、邏輯變數和其他一些信息。其中系統程式是控制PLC實現各種功能的程式,由PLC生產廠家編寫,並固化到唯讀存儲器(ROM)中,用戶不能訪問。輸入單元 輸入單元是PLC與被控...
設計和實現新的超大規模分散式系統架構和標準。參與服務擴容計畫和預測服務增長趨勢,對軟體和系統性能進行調優。提供線上諮詢服務和現場解決問題服務。構建自動運維平台,解決日常問題。構建知識庫,預測可能的問題。XX:運維即生產環境以及和...
鄧小平理論曾經對這個理論主題進行了第一次比較系統的理論思考和初步回答。“三個代表”重要思想回答了“建設什麼樣的黨、怎樣建設黨”的問題,科學發展觀則回答了“實現什麼樣的發展、怎樣發展”的問題,是在鄧小平理論的基礎上進一步深化...
在MRP 管理系統的基礎上,系統增加了對企業生產中心、加工工時、生產能力等方面的管理,以實現計算機進行生產和排產的功能,同時也將財務的功能囊括進來,在企業中形成以計算機為核心的閉環管理系統,這種管理系統已能動態監察到產、供、銷的全...
著重分析和研究人、機、環境三個要素對系統總體性能的影響,如系統中人和機的職能如何分工;如何配合;環境如何適應人;機對環境又有何影響等問題,經過不斷修正和完善三要素的結構方式,最終確保系統最優組合方案的實現。
Windows 自己就將一些主要的系統功能以 DLL 模組的形式實現。一般來說,DLL 是一種磁碟檔案,以.dll、.DRV、.FON、.SYS 和許多以 .EXE 為擴展名的系統檔案都可以是 DLL。它由全局數據、服務函式和資源組成,在運行時被系統載入到...
代碼中的第3到第5個字元告訴你發生故障的系統。1號和2號為燃油或空氣什量問題,3號為點火問題或發動機缺火4號為輔助排放控制,5號與怠速控制問題有關,6號為電腦或輸出電路故障,7號和8號與變連箱問題有關(見更後的有關排放的...
