基本介紹
- 中文名:余代數
- 外文名:coalgebra
- 所屬學科:代數
- 性質:代數的對偶概念
- 產生方式1:對角映射
- 產生方式2:增廣
簡介
定義
代數



余代數研究背景










代數是數學的一個分支。傳統的代數用有字元 (變數) 的表達式進行算術運算,字元代表未知數或未定數。如果不包括除法 (用整數除除外),則每一個表達式都是一個含有理係數的多項式。代數方法使問題的求解簡化為符號表達式的操作,已...
余代數同態(coalgebra morphism)是代數同態的對偶概念。對偶是凸集幾何的一個重要概念。同態是模型論用語。指兩個模型間的同態映射。余代數是代數的對偶概念。設C是R模,Δ是一個R線性映射C→CRC,被稱為余乘法或對角映射;ε是一個R...
余代數張量積是代數張量積的對偶概念。定義 余代數張量積(tensor product of coalgebras)代數張量積的對偶概念.設(C.',4},}}.)和(D,}n}En)是R上的兩個余代數.定義兩個R線性映射:從而,(C⑧ad, }}} } Ec'}D)也是一個余代...
余自由余代數(cofree coalgebra)一類余代數.它與向量空間密切相關。定義 設V是域R上的向量空間.一個對(C,二),其中C是R上的余代數,二:C-> V是R線性映射,若對R上任意的余代數D和任意的R線性映射f:D->V,存在惟一的余...
《余代數框架下的近似行為等價理論與模態邏輯研究》是依託南京航空航天大學,由朱朝暉擔任項目負責人的面上項目。項目摘要 本項目旨在針對當前轉換系統近似等價以及余代數模態邏輯等研究領域中所面臨的問題,探討帶量化信息的余代數的近似行為...
霍普夫代數是20世紀60年代以後迅速發展起來的代數學的新學科。域k上的霍普夫代數是同時具有k代數結構和它的對偶結構(k余代數結構)並滿足一定的相容條件的代數系統。霍普夫代數同態(Hopf algebra homomor-phism)是指滿足特定條件的雙代數...
《Hopf群余代數的相關作用》是2020年5月電子工業出版社出版的圖書,作者是陳全國。內容簡介 本書介紹Hopf群余代數的基礎知識和最新研究成果. 全書共分八章,第一章是必要的概念及準備,第二、三、四章分別介紹擬三角Hopf群余代數和余...
《代數學中的Frobenius結構》共分12章,前面8章主要論述Frobenius結構在一個域上的代數中的運用。尤其是總結了其一般情形的Frobenius環、quasi-Frobenius環的一系列重大進展。後面4章論述了Frobenius結構在一個域上的余代數和Hopf代數中的...
在數學中,霍普夫代數是一類雙代數,亦即具有相容的結合代數與余代數結構的向量空間,配上一個對極映射,後者推廣了群上的逆元運算。霍普夫代數以數學家海因茨·霍普夫命名,此類結構廣見於代數拓撲、群概形、群論、量子群等數學領域。定義...
《路余代數上的雙代數結構和Artin代數的有限維數》是依託山東大學,由張愛平擔任項目負責人的青年科學基金項目。中文摘要 在Hopf代數理論中,箭圖Hopf代數的推廣問題一直是一個熱點問題。當一個箭圖的頂點集有群結構時,對應的路余代數...
首先研究 Cend(M) 和自由結合共形代數 CF(B,N) 的Hochschild上同調和循環上同調,做好基礎和鋪墊工作;其次探討交換結合共形代數的Hochschild上同調和循環上同調的Hodge分解,並研究這兩個上同調的代數和余代數結構;最後研究結合共形代數...
我們首先研究量子擬shuffle代數的代數結構:利用混合shuffle的概念,我們得到了量子擬shuffle乘積的具體公式,並給出了由量子擬shuffle雙代數的本原元生成的子代數的一個完整描述;我們構造了量子擬shuffle代數的對偶余代數結構,在交換辮子Rota...
並將絕對n-完全代數與Abel群McKay箭圖的關係部分推廣到n-完全代數。還給出n-阿貝爾範疇的同調代數。給出了內射Hom-模的Baer準則,證明了HomMod是一個Abelian範疇;確定了Morita-Takeuchi余代數上所有Gorenstein內射余模及Gorenstein余代數的...
代數 代數是集合論的一個概念。定義 代數是在有限的交與補下閉的非空集類。性質 代數為包含單位元X的環。
項目組成員還在典範雙模的同調性質與控制維數、對稱代數上生成子的自同態代數成為廣義對稱代數、Schur代數上的Doty余代數結構和控制維數等取得重要成果,在頂尖刊物上發表。還有成員解決了馴順型代數的模範疇的齊性的Crawley-Boevey猜想,已被...
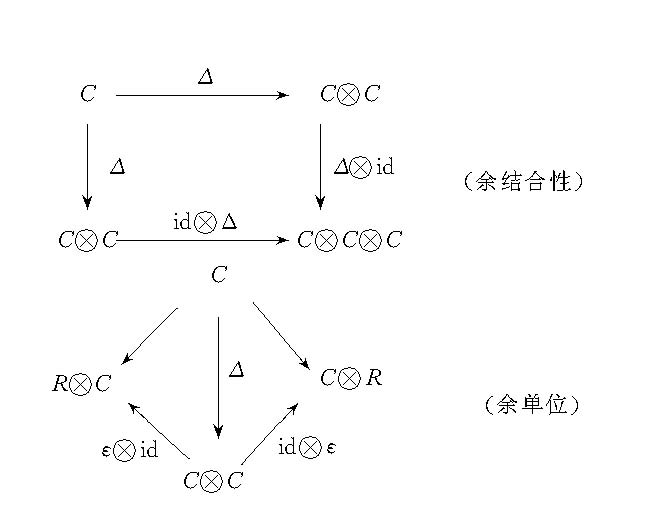
余代數 余代數(coalgebra)是代數的對偶概念。設 C 是 R 模, Δ 是一個 R 線性映射 C→CC ,被稱為余乘法或對角映射; ε 是一個 R 線性映射 C→R ,稱為余單位元或增廣。R上的余代數是指滿足以下二交換圖的三元組(C,...
這一結構定理是真正在Hopf代數意義下的結構定理,它突破了原有的余代數意義下相應定理,使得Hopf代數對映階數的計算通過轉移變得比較容易,此時,自由二次雙代數的結構也能由余模、Grothendieck群進行分類。(3)郝志峰在Hopf代數的同調理論...
雙邊余理想(two-sided coideal)是使得商空間仍為余代數的子空間。設(C,Δ,ε)是R余代數,V為C的R子模。若V滿足Δ(V)VC+CV和ε(V)=0,則稱V為雙邊余理想。概念 雙邊余理想(two-sided coideal)是使得商空間仍為余代數的...
子余模 子余模是一個數學術語。定義介紹 子余模(sub-comodule)余模的一個特殊R子模.它是子模的對偶.(C,。,。)是R上的余代數,(M,p)是右C余模.M的一個R子模N,若滿足p(N) cN⑧KC,則稱N為M的子余模.
