基本介紹
概念介紹,對偶,同態,余代數,模同態,其他同態及性質,雙代數同態,霍普夫代數同態,非結合代數的同態基本定理,
概念介紹
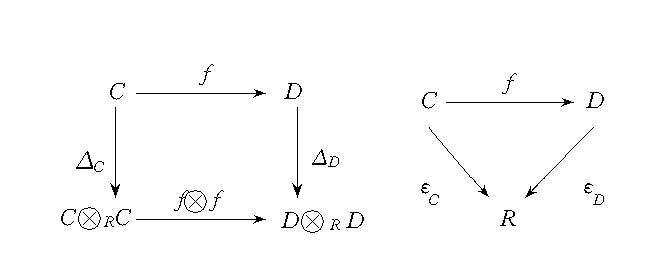 余代數同態
余代數同態則稱f為(C,ΔC,εC)到(D,ΔD,εD)的余代數同態。
對偶
凸集幾何的一個重要概念。它是與凸集的配極和凸包絡有關的概念。若X是一個歐幾里得空間,取X中有限個點(ai)i=1,2,…,n,且Q=ε(a1,a2…,an)是(ai)i=1,2,…,n的凸包絡,則凸集Q(即Q的配極)是一個凸多面體。若還有O∈Q,則Q是一個多胞形,稱Q是Q的對偶。Cubd的對偶是Cocd;Cocd的對偶是Cubd。若Q是歐幾里得空間X中的一個多胞形O∈Q,則O∈Q,且Q亦為多胞形,稱Q是Q的對偶。由對偶方法可知:一個多胞形P的頂點個數是有限的,則P是它們的凸包絡.反過來,有限多個點的凸包絡是一個緊的凸多面體。
同態
設E與F為兩個群胚,它們的合成法則分別記為⊥與⊤. 稱從E到F中的映射f是群胚同態,如果對於E的任一元素偶(x,y),有:

設G為乘法群,而a為G的元素. 由關係f(n)=an所定義的從加法群Z到G中的映射f是群的同態.
設A與B為兩個環(兩個體),稱從A到B中的映射f是環(體)的同態,如果f是加法群的同態,且為乘法么半群的同態. 這就是說,對A的任一元素偶(x,y),有:
f(x+y)=f(x)+f(y)f(xy)=f(x)f(y),
並且f將A的單位元變成B的單位元.
例如,設n為非零自然數;使任一有理整數對應其對模n的剩餘類映射是從環Z到環Z/nZ上的同態.設E與F為兩個A-代數(兩個酉A-代數). 稱從E到F中的映射f是A-代數(酉A-代數)的同態,如果它是線性映射,並且是乘法群胚(乘法么半群)的同態.
例如,設E為交換體K上的非零有限n維向量空間,而B為E的基. 則從E的全體自同態之酉代數ℒ(E)到K中元素構成的全體n階方陣之酉代數Mn (K)中的映射,如果該映射使E的任一自同態對應它在基B中的矩陣,則這一映射是酉代數的同態.
同態的概念能用抽象的方式加以推廣.
余代數
代數的對偶概念。設C是R模,Δ是一個R線性映射C→CRC,被稱為余乘法或對角映射;ε是一個R線性映射C→R,稱為余單位元或增廣。R上的余代數是指滿足以下二交換圖的三元組(C,Δ,ε):
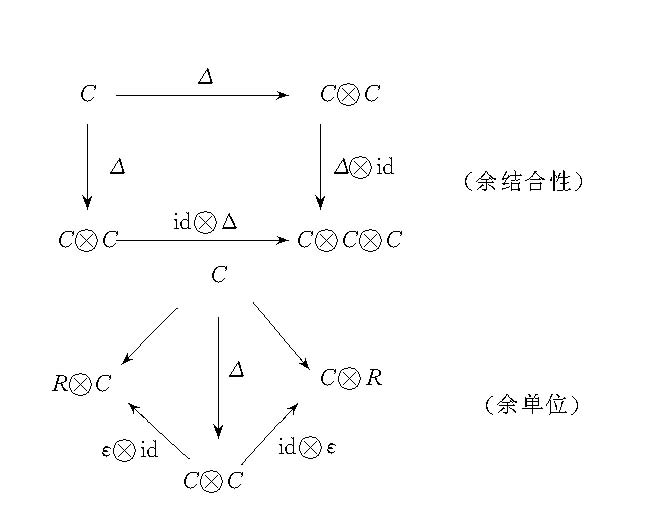 余代數
余代數模同態
模同態是模論的重要概念之一。指兩個模之間的一類映射。設M,N是兩個A模,f是加群M到N的群同態,若f還保持A到M,N上的運算,即對任意a∈A,f(ax)=af(x),x∈M,則稱f是模同態,也稱A同態.常記為f∈HomA(M,N)或f∈Hom(M,N)。任意兩個模M,N之間總存在模同態,例如,設f(x)=0,x∈M,通常稱此同態為零同態。若N是M的子模,映射π:x→x-=x+N是AM到AM-的模同態,則稱π為自然同態.模M,N之間的模同態集HomA(M,N)是一個加群,特別地,當M=N時,記
End(AM)=HomA(M,N),
它是一個環,稱為模M的自同態環.A是End(AM)的子環。
其他同態及性質
雙代數同態
具有雙重同態性質的映射。設B和B′是R上的兩個雙代數,若一個B到B′的代數同態f同時又是余代數同態,則f稱為B到B′的一個雙代數同態。
霍普夫代數同態
滿足特定條件的雙代數同態。設(H,μ,η,Δ,ε,S)和(H′,μ′,η′,Δ′,ε′,S′)是R上的兩個霍普夫代數。若f是(H,μ,η,Δ,ε)到(H′,μ′,η′,Δ′,ε′)的一個雙代數同態,並且S′·f=f·S,則f稱為霍普夫代數同態。
非結合代數的同態基本定理
描述一般非結合代數同態像性質的重要定理。其敘述是:若A是域F上的一個非結合代數,B是A的一個理想,則商代數A/B是A在自然同態a→a+B,a∈A,a+B∈A/B下的同態像;反之,若A′是同態映射a→a′(a∈A,a′∈A′)的同態像,則A′同構於商代數A/B,其中B是同態映射的核。
