基本介紹
概念介紹
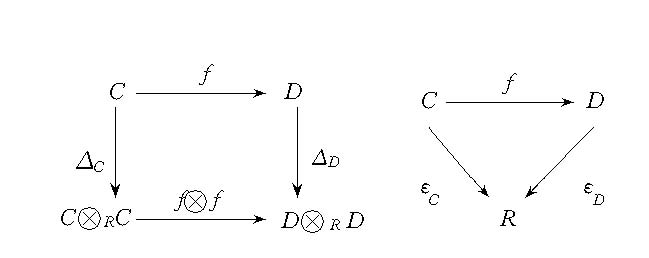 余代數同態
余代數同態對偶
同態
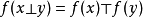
余代數
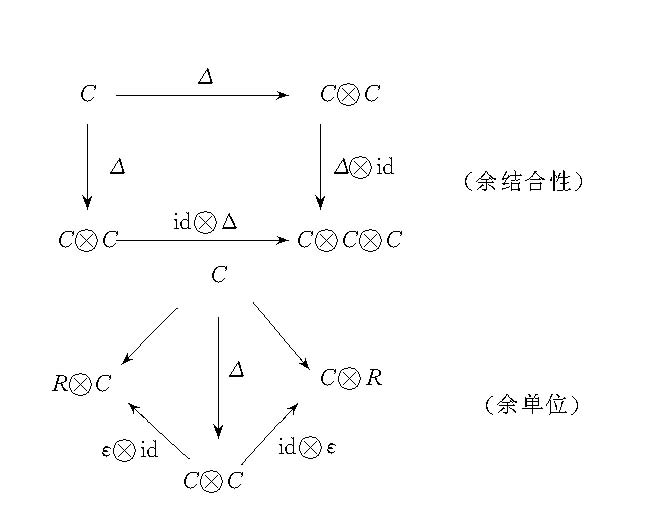 余代數
余代數 余代數同態
余代數同態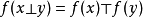
 余代數
余代數余代數同態(coalgebra morphism)是代數同態的對偶概念。對偶是凸集幾何的一個重要概念。同態是模型論用語。指兩個模型間的同態映射。余代數是代數的對偶概念。設C是...
霍普夫代數是20世紀60年代以後迅速發展起來的代數學的新學科。域k上的霍普夫代數是同時具有k代數結構和它的對偶結構(k余代數結構)並滿足一定的相容條件的代數系統。...
余模同態(comodule homomorphism)是模同態概念到余模的引申。設(M,ρM)和(N,ρN)是R上余代數(C,Δ,ε)上的兩個余模。若一個R模同態f:M→N使右圖交換...
余自由余代數(cofree coalgebra)一類余代數.它與向量空間密切相關。...... 若對R上任意的余代數D和任意的R線性映射f:D->V,存在惟一的余代數同態F使右圖交換,...
商余代數(quotient coalgebra)是商代數的對偶概念。...... 商代數的對偶概念.設(C,},e)是R上的一個余代數,V是C的一個雙邊余理想,二是C到C/V的R模同態....
設E與F為兩個A-代數(兩個酉A-代數)。稱從E到F中的映射f是A-代數(酉A-代數)的同態,如果它是線性映射,並且是乘法群胚(乘法么半群)的同態。...
設(B,μ,η)是R代數,且(B,Δ,ε)是R上的余代數,其中μ是B的乘法映射,η是刻畫B的單位元的映射。若Δ和ε都是R代數同態(等價於μ,η都是R余代數同態)...
,存在唯一確定的群同態 ,如果 ,就稱兩個代數閉鏈 和 是同調等價的 (homologically equivalent)(記為 )。同調等價於 0 的代數閉鏈的子群記為 。存在嵌入 。...
眾所周知,一個代數的模與代數的表示,即代數到一個全矩陣代數的同態像是一回事。如果我們把這樣的一個同態像看作是原來代數的一張照片,則有限表示型代數是用有限...
第二章 研究了由濾子生成的同餘關係,以及Heyting代數同態和同構定理。首先,在Heyting代數中定義了關於濾子的一個等價關係,並證明它是同餘關係,以及Heyting代數關於...
3.4.1商空間與同態基本定理3.4.2直和與投影變換習題3第4章 矩陣、線性方程...5.1.1代數5.1.2一元多項式代數5.1.3帶餘除法5.1.4整除與同餘5.2多項式...
《套用近世代數》是2006年清華大學出版社出版的圖書,作者是王殿軍。[1] 本書...1. 同構與同態1292. 有關同態的一些定理1303. 分式域132習題3.3 133...
而且,導子在域K的加法下是一同態如果K 是一個微分域,那么我們定義常數域為 。微分代數微分代數 編輯 一個域 K 上的微分代數是一個 K-代數 A,其中導子與域...
布爾否定,布爾代數的余運算等.布爾代數的運算符號也有別種記法,如∪,∩,-;∨...同態的逆也是同態,我們稱兩個布爾代數 A 和 B 為同態的。從布爾代數理論的...
《近世代數及其套用》是2016年北京郵電大學出版社出版的圖書,作者是羅守山。[1]...1.6.3同態密碼算法37小結43習題43第2章群452.1群的定義與性質46...
《清華大學研究生公共課教材·數學系列·套用近世代數》是2006年清華大學出版社...1. 同構與同態1292. 有關同態的一些定理1303. 分式域132習題3.3133...
可以證明,代數數論是一滿同態。令K1為這個同態的核,顯然,【D1:K1】=ƒ,│K1│=e,D1稱為Q1的分解群,K1稱為Q1的惰性群。對Qi相應地有子群Di與Ki, 在g...
《近世代數講義》根據作者在復旦大學多年教學的講義修改而成,內容包括群的基本...2.3 環的同態2.4 域的基本知識第3章 多項式和有理函式3.1 單變數多項式...
計算機代數(Computer Algebra)在很多時候又被廣義地理解為“符號計算”(Symbolic ...4.1 多項式餘式序列與最大公因子4.2 子結式多項式餘式序列4.3 同態像與模方法...
定義 右余模(right comodule)模的對偶概念.設(C,},e)是一個R上的余代數,M是R上模.若有R模同態p: M->M⑧KC使下面兩圖交換,則(M,戶稱為右余模,p...
同構基本定理,即同態基本定理,由埃米·諾特提出。包含三個定理,在泛代數領域有廣泛的套用,證明了一些自然同構的存在性。...
它揚棄傳統的關於余交換情形下的代數K理論的結構定理,因而很好地解決了Grothendick群在Hopf代數同態意義下的階數估計,且大大地超過國外同類的研究成果,使國外的相應...
一個代數結構必定與它的商代數同態,把任一元素對應到這個元素所在的等價類的映射就是代數結構到其商代數的同態映射。反過來,代數結構A的任何一個同態映射可以導出A...
同構基本定理或稱同態基本定理,包含三個定理,在泛代數領域有廣泛的套用。它們證明了一些自然同構的存在性。歷史同構基本定理最早由埃米·諾特(Emmy Noether)在她於...
在數學中,群表示一個擁有滿足封閉性、結合律、有單位元、有逆元的二元運算的代數結構,包括阿貝爾群、同態和共軛類。...
