伴隨行列式(adjoint determinant),與原行列式密切相關的一個行列式。


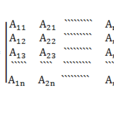
伴隨行列式(adjoint determinant),與原行列式密切相關的一個行列式。


線上性代數中,一個方形矩陣的伴隨矩陣是一個類似於逆矩陣的概念。如果二維矩陣可逆,那么它的逆矩陣和它的伴隨矩陣之間只差一個係數,對多維矩陣不存在這個規律。...
伴隨行列式(adjoint determinant),與原行列式密切相關的一個行列式。...... 伴隨行列式(adjoint determinant),與原行列式密切相關的一個行列式。設n階行列式...
伴隨陣,又稱伴隨矩陣(adjoint matrix)。設R是一個交換環,A是一個以R中元素為係數的 n×n 的矩陣。A的伴隨矩陣可按如下步驟定義:定義1:A關於第i 行第j ...
伴隨表示(adjoint representation)是代數群的一種表示,指代數群在它的李代數上的一個典範表示。設G是代數群,g是它的李代數,G在g上的伴隨表示定義為Ad:G→Aut(...
經典伴隨變換(classical adjoint transformation)是向量空間中的一種線性變換。線上性代數中,一個方形矩陣的伴隨矩陣是一個類似於逆矩陣的概念。如果矩陣可逆,那么它的...
矩陣行列式是指矩陣的全部元素構成的行列式,設A=(aij)是數域P上的一個n階矩陣,則所有A=(aij)中的元素組成的行列式稱為矩陣A的行列式,記為|A|或det(A)。若...
行列式在數學中,是由解線性方程組產生的一種算式。行列式的特性可以被概括為一個多次交替線性形式,這個本質使得行列式在歐幾里德空間中可以成為描述“體積”的函式。...
行列式的階越低越容易計算,於是很自然地提出,能否把高階行列式轉換為低階行列式來計算,為此,引入了餘子式和代數餘子式的概念。在n階行列式中,把所在的第i行與...
證明設B(λ)是矩陣λE-A的伴隨矩陣,則:B(λ)(λE-A)=|λE-A|E=f(λ)E. (2)因為B(λ)的元素是|λE-A|的元素的代數餘子式,所以B(λ)的元素...
有的時候,當矩陣的階數比較高的時候,使用其行列式的值和伴隨矩陣求解其逆矩陣會產生較大的計算量。這時,通常使用將原矩陣和相同行數(也等於列數)的單位矩陣並排...
adj是一個線性代數術語。在矩陣理論中,adj表示一個矩陣的伴隨矩陣;線上性代數中,一個方形矩陣的伴隨矩陣是一個類似於逆矩陣的概念。如果矩陣可逆,那么它的逆矩陣...
在向量微積分中,雅可比矩陣是一階偏導數以一定方式排列成的矩陣,其行列式稱為雅可比行列式。雅可比矩陣的重要性在於它體現了一個可微方程與給出點的最優線性逼近。...
整數矩陣(integer matrix)是在數論中有重要套用的一種矩陣,指元素aij(i,j=1,2,…,n)都是整數的n階矩陣A=(aij),若n階整數矩陣A的行列式|A|=±1,則A稱...
從向量的幾何意義開始,分別講述了向量組、向量空間、行列式、矩陣、線性方程組和...5.14.3 伴隨矩陣的幾何意義 2135.14.4 正交矩陣的幾何意義 215...
▪ 第一章 行列式 ▪ 第二章 矩陣 ▪ 第三章 n維向量 ▪ 第四...伴隨矩陣可逆矩陣初等變換矩陣方程四、練習題精選答案與提示線性代數輔導講義第三...
《線性代數題型全攻略》與同濟版《線性代數》同步,包括行列式、矩陣及其運算、矩陣的初等變換與線性方程組、向量組的線性相關性、相似矩陣及二次型、線性空間與線性...
第1章行列式11.1二階、三階行列式11.1.1二階行列式11.1.2三階行列式2...2.3.2矩陣可逆的充要條件、逆矩陣的伴隨矩陣求法392.3.3可逆矩陣的性質42...
2.6 伴隨矩陣的幾個性質的套用2.7 元素沒有具體給出的矩陣行列式算法2.8 抽象方陣的行列式是否等於零的證法2.9 分塊矩陣的運算2.10 方陣高次冪的計算方法與...
2.1.7 方陣的行列式2.1.8 對稱矩陣2.1.9 共軛矩陣2.2 逆矩陣2.2.1 逆矩陣的概念2.2.2 伴隨矩陣及其與逆矩陣的關係2.2.3 矩陣方程...
矩陣正式作為數學中的研究對象出現,則是在行列式的研究發展起來後。邏輯上,矩陣...“方陣式”,而各類矩陣如“正交矩陣”、“伴隨矩陣”中的“矩陣”則被翻譯為...
