伴隨微分方程(adjoint differential equation)是與給定微分方程有共軛關係的微分方程。這種伴隨關係具有對稱性。伴隨微分方程套用很多,例如套用於分析遞推辨識算法收斂性問題的ODE法中,討論辨識算法與伴隨微分方程的關係。
基本介紹
- 中文名:伴隨微分方程
- 外文名:adjoint differential equation
- 定義:與給定微分方程有共軛關係的方程
- 性質:對稱性
- 一級學科:數學
- 二級學科:線性常微分方程
簡介








辨識算法與伴隨微分方程的關係













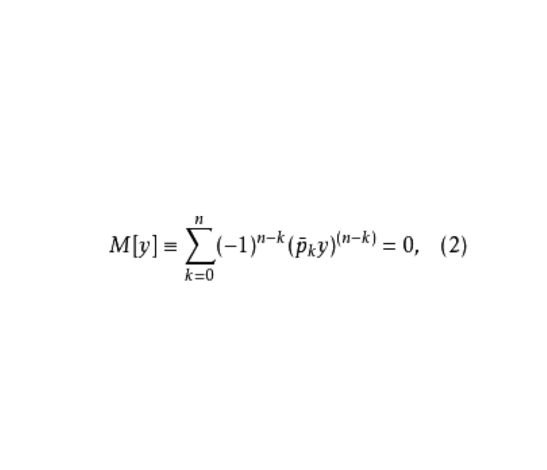
伴隨微分方程(adjoint differential equation)是與給定微分方程有共軛關係的微分方程。這種伴隨關係具有對稱性。伴隨微分方程套用很多,例如套用於分析遞推辨識算法收斂性問題的ODE法中,討論辨識算法與伴隨微分方程的關係。





















伴隨微分方程(adjoint differential equation)是與給定微分方程有共軛關係的微分方程。這種伴隨關係具有對稱性。伴隨微分方程套用很多,例如套用於分析遞推辨識算法收斂性問題的ODE法中,討論辨識算法...
微分方程,是指含有未知函式及其導數的關係式。解微分方程就是找出未知函式。微分方程是伴隨著微積分學一起發展起來的。微積分學的奠基人Newton和Leibniz的著作中都處理過與微分方程有關的問題。微分方程的套用十分廣泛,可以解決許多與導數...
形式伴隨方程(formal adjoint equation)是在Rⁿ中為確定常數變易公式的積分核而導出的相關方程。簡介 形式伴隨方程是在Rⁿ中為確定常數變易公式的積分核而導出的相關方程。具體內容 設線性泛函微分方程ẋ(t)=L(t,xₜ)或 的解...
微分動力學系統 微分動力學系統(differential dynamical system)是1990年公布的數學名詞。公布時間 1990年,經全國科學技術名詞審定委員會審定發布。出處 《自動化名詞》第一版。
微分方程是伴隨著微積分學一起發展起來的。微積分學的奠基人Newton和Leibniz的著作中都處理過與微分方程有關的問題。微分方程的套用十分廣泛,可以解決許多與導數有關的問題。物理中許多涉及變力的運動學、動力學問題,如空氣的阻力為速度...
真實伴隨運算元(true adjoint operator)是在C([-r,0],Rⁿ)中為確定常數變易公式而導出的相關運算元。簡介 真實伴隨運算元是在C([-r,0],Rⁿ)中為確定常數變易公式而導出的相關運算元。具體內容 設齊次與非齊次線性泛函微分方程的解...
微分方程是伴隨著微積分學一起發展起來的。微積分學的奠基人Newton和Leibniz的著作中都處理過與微分方程有關的問題。微分方程的套用十分廣泛,可以解決許多與導數有關的問題。物理中許多涉及變力的運動學、動力學問題,如空氣的阻力為速度...
《微分結式理論及其在微分方程求解中的套用》是依託北方工業大學,由張智勇擔任項目負責人的青年科學基金項目。項目摘要 隨著對稱群理論和方法在微分方程(組)求解中的廣泛套用,人們需要更加深入系統地分析和把握對稱的性質,特別是關於偏微分...
《微分方程與線代數》是2014年東南大學出版社出版的圖書。內容簡介 《微分方程與線性代數/21世紀獨立本科院校規劃教材》是普通高校“獨立學院”本科“微分方程與線性代數”課程的教材,包含常微分方程、行列式與矩陣、向量與線性方程組、特徵...
第3章 線性微分方程組的解法 第4章 常微分方程的運算元解法 第5章 常微分方程的數值解法及其C程式設計 第6章 Maple軟體在解常微分方程中的套用 第7章 常微分方程的建模套用 前言 常微分方程是在17世紀伴隨著微積分而發展起來的一門...
微分幾何是運用微積分的理論研究空間的幾何性質的數學分支學科。古典微分幾何研究三維空間中的曲線和曲面,而現代微分幾何開始研究更一般的空間---流形。微分幾何與拓撲學等其他數學分支有緊密的聯繫,對物理學的發展也有重要影響。愛因斯坦的...
《微分方程與線性代數》是2014年東南大學出版社出版的圖書。內容簡介 《微分方程與線性代數/21世紀獨立本科院校規劃教材》是普通高校“獨立學院”本科“微分方程與線性代數”課程的教材,包含常微分方程、行列式與矩陣、向量與線性方程組、...
(4)微分運算元也服從移位定理(shift theorem),即 套用 在物理科學的套用中,像拉普拉斯運算元在建立與求解偏微分方程中起著主要的作用。在微分拓撲中,外導數與李導數運算元有內蘊意義。在抽象代數中,導子的概念是微分運算元不要求分析的一...
2.微分方程.早在都靈時期,拉格朗日就對變係數常微分方程研究做出重大成果.他在降階過程中提出了以後所稱的伴隨方程,並證明了非齊次線性變係數方程的伴隨方程的伴隨方程,就是原方程的齊次方程.他還把歐拉關於常係數齊次方程的結果...
《關於黑洞形成的數學理論》是依託清華大學,由於品擔任項目負責人的青年科學基金項目。項目摘要 伴隨著偏微分方程的技術的發展,尤其是對引力場方程的進一步認識,現在人們已經可以從數學上嚴格的研究黑洞形成的一些基本機制,比如說2008年...
微分方程 早在都靈時期,拉格朗日就對變係數常微分方程研究做出重大成果。他在降階過程中提出了以後所稱的伴隨方程,並證明了非齊次線性變係數方程的伴隨方程的伴隨方程,就是原方程的齊次方程。他還把歐拉關於常係數齊次方程的結果推廣到...
3.7.1 常微分方程的伴隨方程 3.7.2 施圖姆-劉維爾運算元 3.7.3 非自伴二階常微分方程的完備集 3.8 非齊次方程有解的條件 習題 附錄3A 初值問題(3.1.4)的解的存在唯一性的證明 附錄3B 二重求和中變數的代換 附錄3C 關於...
最大值原理不同於經典情形,一階伴隨方程為平均場倒向隨機微分方程。以遞歸效用為基礎,研究了平均場正倒向隨機控制系統的最佳化問題。用極限方法研究了平均場反射倒向隨機微分方程,研究了平均場反射倒向隨機微分方程和相關帶障礙的非局部...
廣義解(generalized solution)亦稱弱解,偏微分方程經典解的推廣。按經典的意義來說,微分方程的解應當具有原方程中出現的那些導數,但有時這樣的要求顯得過嚴,會給問題的討論帶來不便,為此需要把解的概念加以推廣。例如,可以將廣義解看...
微分方程是伴隨著微積分學一起發展起來的。微積分學的奠基人Newton和Leibniz的著作中都處理過與微分方程有關的問題。微分方程的套用十分廣泛,可以解決許多與導數有關的問題。物理中許多涉及變力的運動學、動力學問題,如空氣的阻力為速度...
3.6.1拉格朗日方程的自伴隨性(102)3.6.2由自伴隨運動微分方程構造拉格朗日函式(104)3.6.3根據運動微分方程的結構特點構造拉格朗日函式(107)3.6.4利用運動微分方程第一積分構造拉格朗日函式(108)3.7在與速度有關的力作用下系統的...
例如,對區域Ω 上對偏微分運算元 L,如果 且存在函式序列 滿足 則稱 u 為方程 Lu=f 的 L² 強解。對偏微分方程 Lu=f 對定解問題,如果 uₙ 還滿足相應解條件,則稱 u 是相應定解問題 L² 強解。對同一定解問題,...
現在比較常用的幾種直接求解方法包括最優參數控制法,有限差分方法,配點法,微分包含方法和偽譜方法。在最優參數控制法中,控制量被單獨參數化,同時數值積分方法被用來求解微分方程;在有限差分方法中,原微分方程和邊界條件被近似為有限差...
