廣義解

廣義解(generalized solution)亦稱弱解，偏微分方程經典解的推廣。按經典的意義來說，微分方程的解應當具有原方程中出現的那些導數，但有時這樣的要求顯得過嚴，會給問題的討論帶來不便，為此需要把解的概念加以推廣。例如，可以將廣義解看成經典解在一定的函式空間中的極限；也可以按廣義函式滿足原偏微分方程的意義來定義廣義解。

基本介紹

• 中文名：廣義解
• 外文名：generalized solution
• 所屬領域：數學（偏微分方程）
• 相關概念：偏微分方程、經典解、強解等

基本介紹

古典解中對解的光滑性要求太強了，而為了使解能滿足這樣的光滑性，又要對定解問題中的初值、邊值、係數、非齊次項等加上很強的光滑性。從物理上看，這些條件似乎過於人為，在具體套用時，帶來一定的束縛。甚至有些物理上提出的很簡單的定解問題，在嚴格的古典解定義下都是無解的。因此,必須放鬆對解的光滑性的要求，擴大定義解的函式類.擴大了解的函式類以後得到的解稱為廣義解。

許多描述實際物理現象的偏微分方程定解問題不可能有經典解。例如，當ψ∈C²(R)時，弦振動方程柯西問題

有唯一解

如果弦的初始狀態呈折線，即ψ(x)連續但在一些點上沒有導數，則由(3)給出的u(x，t)只在ψ有二階導數的那些點上滿足方程(1)，它不是柯西問題(1)，(2)在經典意義下的解，但它卻是在初始狀態(1)下弦的真實物理狀態，因此稱它為柯西問題(1)，(2)的廣義解。

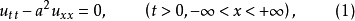
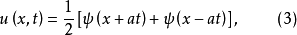
定義廣義解的方法

對不同的偏微分方程定解問題(甚至對同一定解問題)，可以有不同的廣義解定義，但它們都是經典解的推廣，因此，經典解必定是廣義解，現代定義廣義解的方法主要有兩種：一種是將經典解序列在某個函式空間中的極限定義為廣義解，稱為強解；一種是通過所給偏微分運算元的共軛(伴隨)運算元來定義廣義解，稱為弱解。

定義廣義解的原則

具體定義廣義解的方式有很多種，通常有兩個原則：

(1)古典解必是廣義解；

(2)廣義解是唯一的，且按某種度量連續依賴於定解數據。

例如考慮泊松方程的狄利克雷向題

如果存在一個函式(表示函式絕對值的p次方在勒貝格積分的意義下可積的函式類)，對於所有的都有則稱u為原定解問題的L'-弱解。L'-弱解是一種重要的廣義解。

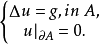
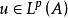
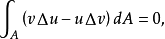
廣義解稱為古典解的推廣，自然應滿足以下三點：

(1) 古典解必為廣義解；

(2) 當廣義解具有古典解所要求的光滑性時，則它一定是古典解；

(3) 廣義解是適定的。