弱解

數學中， 微分方程的弱解或廣義解是指對該方程中的微分可能不存在，但是在某種精確定義的意義下滿足該方程的解。

基本介紹

• 中文名：弱解
• 外文名：weak solution
• 套用學科：數學
• 相關術語：廣義解
• 所屬領域：微分方程
• 套用領域：廣義函式

描述

數學中，微分方程的弱解或廣義解是指對該方程中的微分可能不存在，但是在某種精確定義的意義下滿足該方程的解。對於不同種類的微分方程，弱解的定義性質也可能不同。 一類最重要的弱解基於廣義函式的記號。

由於大量用於描述現實世界中現象的微分方程並不具有足夠的光滑的解，從而求解此類方程只能使用弱形式。即使在方程確實具有可微解的情況下，首先證明弱解的存在性然後證明弱解足夠光滑是方便的。

例子

作為弱解的說明，考慮一階波動方程。

(其中的記號請參閱偏導數)其中u=u(t,x) 是兩個實變數的函式。假設u在歐式空間R上連續可微，在方程的兩側同時乘以一個具緊支集的光滑函式φ並積分。得到：

使用富比尼定理和分部積分, 該方程化為

以上的陳述表明：如果u連續可微，方程 (1) 蘊含方程 (2)。弱解概念的關鍵在於存在函式u對任何φ滿足方程 (2)，而這樣的u可能不可微，從而不滿足方程 (1)。該方程的一個簡單的例子是u(t,x) = |t−x| 。(容易證明u滿足方程 (2).) 方程 (2) 的解u被稱作方程 (1) 的弱解。

一般情況

當求解關於u的偏微分方程時，可以利用所謂的測試函式φ，使得方程中關於u的任意階導數都轉化為關於φ的分部積分，用這樣的方法， 可以得到原方程的不必可微的解。

上面的方法不只適用於波動方程，事實上，考慮在域R上的開集'W'內定義的線性微分運算元

其中 (α₁,α₂, ...,α_n) 是某有限集N上的多維下標變數, 並且係數關於x足夠光滑。

乘以緊支集上的光滑測試函式φ，並作分部積分後，微分方程P(x, ∂)u(x) = 0 可以寫作

其中微分運算元Q(x, ∂) 滿足

其中

總而言之， 如果原(強)問題是找到一個開集W上的|α'|階可微函式u， 使得

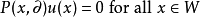
(所謂的強解)，那么可積函式u被稱作弱解。如果

對每個支集W上的光滑函式φ均成立。