偏微分運算元是一類常見而又重要的運算元。它是微分方程中研究的核心對象。
基本介紹
- 中文名:偏微分運算元
- 外文名:partial differential operator
- 適用範圍:數理科學
簡介
線性微分運算元
定義
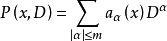

偏微分運算元是一類常見而又重要的運算元。它是微分方程中研究的核心對象。
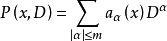

偏微分運算元是一類常見而又重要的運算元。它是微分方程中研究的核心對象。...... 偏微分運算元是一類常見而又重要的運算元。它是微分方程中研究的核心對象。中文名 偏微分...
在數學中,微分運算元是定義為微分運算之函式的運算元。首先在記號上,將微分考慮為一個抽象運算是有幫助的,它接受一個函式得到另一個函式(以計算機科學中高階函式的...
拉普拉斯運算元(Laplace Operator)是n維歐幾里德空間中的一個二階微分運算元,定義為梯度(▽f)的散度(▽·f)。拉普拉斯運算元也可以推廣為定義在黎曼流形上的橢圓型運算元,...
本書共有4卷,作者是世界公認的分析學大師。這套4卷集的經典名著以廣義函式論為框架,論述了與線性偏微分方程理論有關的經典分析和現代分析的核心內容。第2卷內容...
常係數微分運算元(differential operator with constant coefficients)是係數為常數的線性偏微分運算元。賦范向量空間E的連續自同態通常叫做有界運算元,或簡稱為運算元。 定義在...
橢圓型偏微分方程,簡稱橢圓型方程,一類重要的偏微分方程。早在1900年D.希爾伯特提的著名的23個問題中,就有三個問題是關於橢圓型方程與變分法的。八十多年來,...
高階橢圓型偏微分運算元(ellipticpartialdiffe- rential operators of hig her-order)主象徵無非零 實根的線性偏微分運算元.高階微分運算元 則稱運算元P(二,D)在點二...
《擬齊性偏微分運算元的分析》是2007年西北工業大學出版社出版的圖書,作者是羅學波//鈕鵬程//韓亞洲。...
傅立葉積分運算元(Fourier integral operator)是偏微分運算元理論中的重要工具。它和擬微分運算元一起,被稱為“70年代技術”。擬微分運算元的前身是具強奇性的卷積型奇異...
A滿足條件supp Au C supp u,那么稱A為局部運算元.顯然,任一具C00 (,(Z> 係數的微分運算元都是局部運算元,但是,擬微分運算元一 般來說不是局部運算元.例如,積分運算元...
線性偏微分方程是一類重要的偏微分方程,關於所有未知函式及其導數都是線性的偏微分方程稱為線性偏微分方程。例如,拉普拉斯方程、熱傳導方程及波動方程都是線性偏微分...
偏微分方程特徵理論是偏微分方程論的一個基本概念。它對研究解的存在、唯一性及其他性質(例如奇性傳播)都有重要的意義。...
線性微分運算元是一類常見而又重要的運算元。它是微分方程中研究的核心對象。...... 線性微分運算元是一類常見而又重要的運算元。它是微分方程中研究的核心對象。...
現代微分運算元理論是20世紀50年代,由米赫林、考爾德倫(Calderon,A.P.)和贊格蒙(Zygmund,A.)等人發展起來的奇異積分運算元理論。...
《線性偏微分運算元分析第1卷第2版》是2005年6月由北京世界圖書出版公司出版的圖書,作者是L.Hormander。...
非線性偏微分方程是各階微分項有次數高於一的微分方程即為非線性偏微分方程,是現代數學的一個重要分支,無論在理論中還是在實際套用中,非線性偏微分方程均被用來...
重調和運算元(multiple harmonic operators 最簡單的高階橢圓型偏微分運算元.若整數k>1,則 稱為重調和運算元. ...
該書提出了一個連貫的、確切的、統一的方法將兩個來自不同領域的元素——泛函分析和偏微分方程,結合在一起,旨在為具有良好實分析背景的學生提供幫助。 通過詳細地...
對於不同的勢函式 V,解這個偏微分方程的即得到定態波函式。 [1] 哈密頓算符哈密頓運算元 編輯 首先,“ ”這個東西具有“雙重性格”,它既是一個矢量,又是一個...
