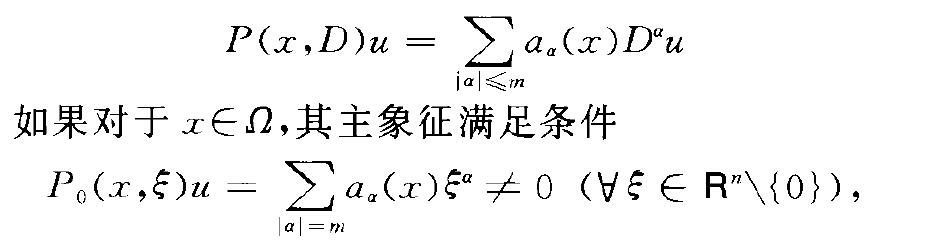
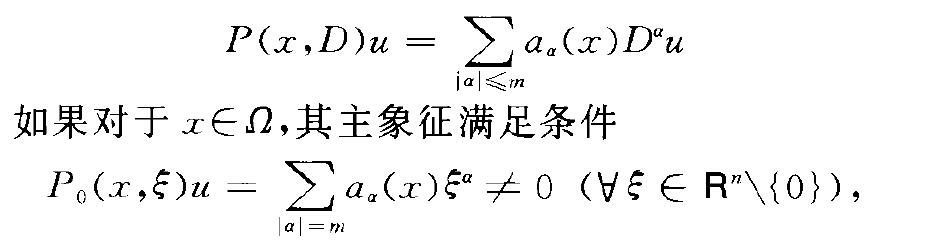
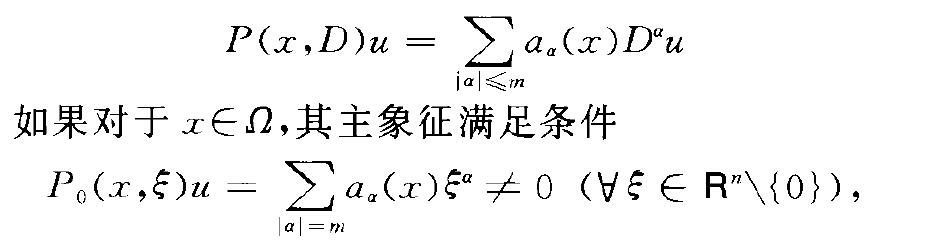
高階橢圓型偏微分運算元(ellipticpartialdiffe- rential operators of hig her-order)主象徵無非零 實根的線性偏微分運算元.高階微分運算元 則稱運算元P(二,D)在點二...
成立的區域內,就稱方程是橢圓型的 [1] 。此時,可以通過自變數的非奇異變換將方程化為標準型對於高階線性方程,設 階線性偏微分運算元為其中...
恰當橢圓型運算元(properly elliptic operators ) 一類重要的橢圓型偏微分運算元.如果運算元 是橢圓型的,並且對於R”中任意兩個線性獨立的向 量寧和引,復變數:的多項式 ...
重調和運算元(multiple harmonic operators 最簡單的高階橢圓型偏微分運算元.若整數k>1,則 稱為重調和運算元. ...
拉普拉斯運算元(Laplace Operator)是n維歐幾里德空間中的一個二階微分運算元,定義為梯度(▽f)的散度(▽·f)。拉普拉斯運算元也可以推廣為定義在黎曼流形上的橢圓型運算元,...
個抽象運算是有幫助的,它接受一個函式得到另一個函式(以計算機科學中高階函式...橢圓型運算元 分數微積分 不變微分運算元 參考資料 1. 張文奎. 微分運算元[J]...
3.2 橢圓型方程邊值問題的可解性3.3 解的正則性3.4 高階橢圓型方程...5.3 運算元半群方法的套用參考文獻 [1] 參考資料 1. 現代偏微分方程導論 ....
將上述討論移到一般的m 階線性偏微分運算元P(x,Dx)上,這裡P(x,Dx)是的...亞橢圓性的研究也是線性偏微分運算元理論的基本問題之一。非線性偏微分方程解的...
橢圓型方程組(system of elliptic equations) 是描述穩定或定常狀態的一類偏微分...是N×N階矩陣,B是階數低於2m的微分運算元,和式對所有足標k1,k2,…,k2m從0...
Kohn-Laplace運算元的基本解、亞橢圓性、譜與特徵值,第二部分擬齊性線性偏微分運算元,內容包括擬齊性偏微分運算元、Liouville定理、解析亞橢圓性、多項式解空間、奇點可去...
二階擬線性橢圓型方程(quasilinear elliptic equations of second order)是關於二階導數為線性且其係數矩陣為正定的二階非線性偏微分方程,非線性偏微分方程是關於(...
橢圓運算元 參見:橢圓型偏微分方程 設D是k維歐式空間上的n階微分運算元。如果p1, ..., pk是其上的坐標函式,那么定義其符號(symbol)是以(p1, ..., pk, q1,...
在數學中,重調和方程是在連續力學領域產生的四階偏微分方程,包括線性彈性理論和斯托克斯流的解。最簡單的高階橢圓型偏微分方程.方程▽ku=0(▽為拉普拉斯運算元,k為...
(Dirichlet)問題之解到邊界的解析部分的解析性,開創了高階橢圓方程組的解析性...上蓬勃發展的一般偏微分運算元理論,包括擬微分運算元,傅立葉積分運算元和馬斯洛夫(...
,其中∇²為拉普拉斯運算元,此處的拉普拉斯方程為二階偏微分方程。三維情況下,拉普拉斯...拉普拉斯方程和泊松方程是最簡單的橢圓型偏微分方程。偏微分運算元 (可以在任意...
他還在1968年得出橢圓型運算元譜函式的精密的漸近估計。他的四卷本《線性偏微分運算元分析》公認為這領域最權威的總結性巨著。在多複變函數論方面,他證明加權L^2空間...
從1985年以來, 線上性偏微分方程的局部可解性、冪零李群上的傅立葉分析和不變偏微分運算元、非線性積分偏微分方程、奇異橢圓型偏微分方程、拋物型偏微分方程、自由...
