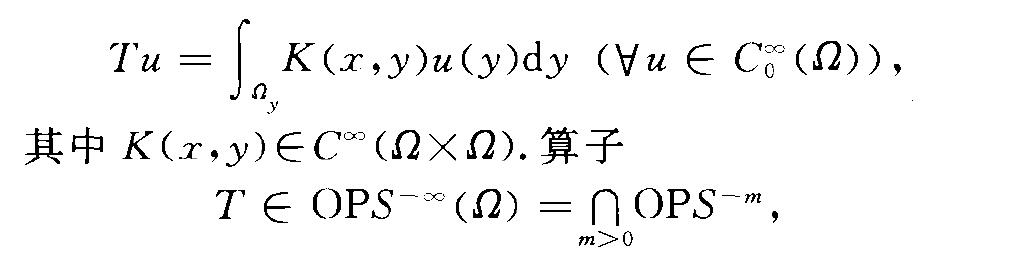
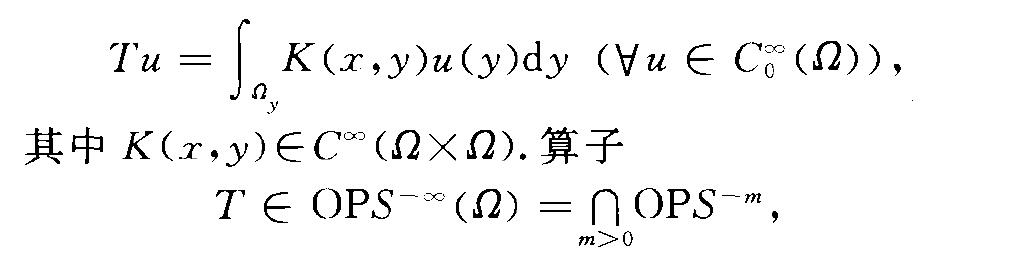
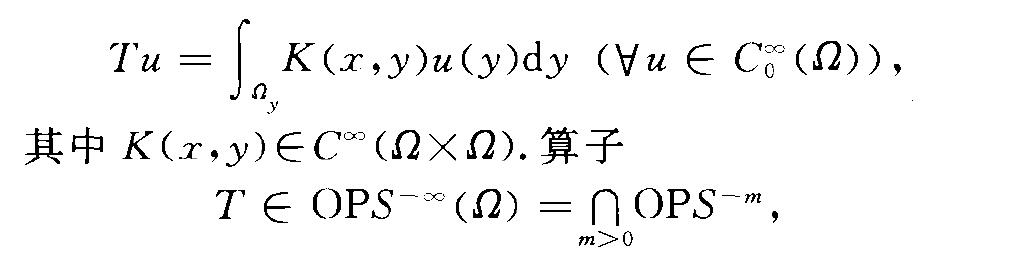
局部運算元(local operators)具有光滑係數微 分運算元的推廣.設,(lCR·是開集.如果Co (,(Z) Co (,(Z)的線性連續運算元A滿足條件supp Au C supp u,那么稱A為...
局部圖像運算元是圖像特徵的局部表達,它反映了圖像上具有的局部特性,適合於對圖像進行匹配,檢索等套用。...
局部圖像運算元是圖像特徵的局部表達,它反映了圖像上具有的局部特性,適合於對圖像進行特徵提取、匹配、檢索等套用領域。...
局部圖像處理運算元是圖像特徵的局部表達,它反映了圖像上具有的局部特性。...... 局部圖像處理運算元是圖像特徵的局部表達,它反映了圖像上具有的局部特性。...
時頻局部化運算元(band-timelimiting operator )把時間和頻率兩個空間放在一起來考慮稱為時一頻相空間.時頻局部化運算元是一種同時實現時間和頻率的局部化的運算元,即...
Roberts運算元,又稱羅伯茨運算元,是一種最簡單的運算元,是一種利用局部差分運算元尋找邊緣的運算元。他採用對角線方向相鄰兩象素之差近似梯度幅值檢測邊緣。檢測垂直邊緣的效果...
SIFT運算元:SIFT運算元是計算機視覺領域非常著名的特徵運算元,它可用於模式識別和影像匹配。...
局部化理論(theory of localization)研究奇異積分方程的一種新方法,即局部化方法的理論,此方法對高維也很有價值.運算元A:L?}LP稱為局部型運算元,若對任意兩個不...
運算元積展開(Operator Product Expansion, "OPE")是共形場論的一種工具,用來計算局部運算元的積的期望值。...
Roberts邊緣檢測運算元是一種利用局部差分運算元尋找邊緣的運算元,Robert運算元圖像處理後結果邊緣不是很平滑。經分析,由於Robert運算元通常會在圖像邊緣附近的區域內 產生較寬的...
局部可解性,是指研究線性偏微分方程Pu=ƒ在什麼條件下局部有解存在。...... 研究線性偏微分方程Pu=ƒ在什麼條件下局部有解存在。若P是常係數運算元,則由基本解...
弱運算元拓撲(weak operator topology)是運算元空間中的一種局部凸拓撲。...... 弱運算元拓撲(weak operator topology)是運算元空間中的一種局部凸拓撲。中文名 弱運算元拓撲 ...
常用的提取方法有邊緣提取法、角點檢測法、興趣運算元法等,方法雖然不同,但基本原則都是選擇局部灰度變化最大點作為特徵點,這樣可以保持特徵點鄰域內的紋理細節,減少...
強運算元拓撲(strong operator topology)是運算元空間中的又一種拓撲。從賦范線性空間X到賦范線性空間Y的有界線性運算元全體所成的賦范線性空間B(X→Y)中由半范族{...
向量微分運算元,Nabla運算元(nabla operator),又稱劈形運算元,倒三角運算元,是一個微分運算元。...
同倫運算元(homotopy operator)是具有同倫性質的線性變換。兩個拓撲空間X和Y同倫等價的充要條件是:存在空間Z,使得X與Y分別同胚於Z的兩個強形變收縮核。倫型相同...
非線性運算元又稱非線性映射,不滿足線性條件的運算元。泛函分析的研究對象主要是線性運算元及其特殊情況線性泛函。但是,自然界和工程技術中出現的大量問題都是非線性的。...
Moravec (1977)是第一個提出興趣點這一概念的人。Moravec 運算元在4 個方向上計算非歸一化的影像局部灰度差方差,將最小值作為興趣值測度。因此,該運算元檢測的特徵點...
在微分幾何中,拉普拉斯運算元可以推廣為定義在曲面,或更一般地黎曼流形與偽黎曼流形上,函式的運算元。這個更一般的運算元叫做拉普拉斯-貝爾特拉米運算元(Laplace–Beltrami ...
圖像處理運算元是對圖像進行處理時所用到的運算元。包括全局特徵描述運算元和局部特徵描述運算元。...
局部表現模(locally presented module)是一種有用的模。若環A是半完全環,則A是序列環的充分必要條件是,每個有限表現左A模是局部表現A模的直和。...
傅立葉積分運算元(Fourier integral operator)是偏微分運算元理論中的重要工具。它和擬微分運算元一起,被稱為“70年代技術”。擬微分運算元的前身是具強奇性的卷積型奇異...
Harris等提出的對Moravec運算元的改進,就是具有旋轉不變性的角點回響測度(即角點回響運算元)。如果在角點區域內的某個像素處回響值R在8個方向上達到局部最大值,則該...
常係數微分運算元(differential operator with constant coefficients)是係數為常數的線性偏微分運算元。賦范向量空間E的連續自同態通常叫做有界運算元,或簡稱為運算元。 定義在...
前三章主要介紹運算元代數中最重要的三類代數Banach代數,C*代數以及vonNeumann代數的基礎知識,第四章至六章介紹近十年來,對於運算元代數與矩陣代數上各種映射的局部特徵...
