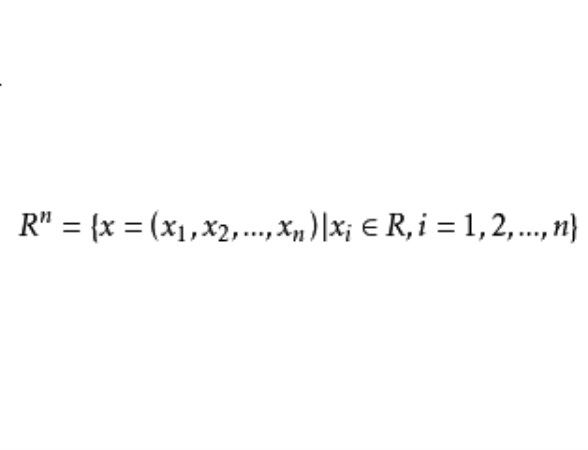n維歐幾里得空間(n-dimensional Euclidean space)是現實空間的抽象與推廣，簡稱n維歐氏空間。n維歐氏空間在代數中是定義了內積的n維線性空間，記為R，其元素是n維向量，即n元有序(實)數值，並利用內積規定向量x的模|x|是其與自身的內積的平方根|x|=√∑i=1xi。在幾何中，借用普通空間中點坐標與其向徑作為以原點為起點的向量的坐標相同之例，也把n維歐氏空間的向量看做點而把n維歐氏空間R看做點空間，因而也可討論R中的幾何圖形，如直線、超平面等。在數學分析中，經常借用代數和幾何中n維歐氏空間的概念，特別是常使用R的向量(元素)x的模|x|的另一名稱範數的概念。在提到x∈R時常只說x是n元數組而不一定提到它是n維歐氏空間的元素，因而還常把x的模，即範數|x|特別稱為x的歐幾里得範數。
基本介紹
- 中文名：n維歐幾里得空間
- 外文名：n-dimensional Euclidean space
- 所屬學科：數學
- 簡稱：n維歐氏空間
- 簡介：現實空間的抽象與推廣
基本介紹,相關概念及性質,
基本介紹
定義1 設n是正整數，由n個實數構成的有序數組
的全體組成的集合，稱為n維點集或n維歐幾里得空間，記作R，即
相關概念及性質
為了深入研究行維點集R中鄰域、有界集、點列收斂等概念，需要對R中的點之間定義距離。為了使問題討論適用於更廣泛的情形，我們對一般的集合給出距離的概念。
定義2 設X是一個非空集合，如果對於X中任何兩個元素x和y，都有一個確定的實數，記為ρ(x，y)，與之對應，且滿足下面三個條件，則稱ρ是X上的一個距離，稱ρ(x，y)是x和y之間的距離，而稱X是以ρ為距離的距離空間(或度量空間)，記為(X，ρ)。這三個條件是：
(1)非負性，ρ(x，y)≥0，而且ρ(x，y)=0若且唯若x=y；
(2)對稱性，ρ(x，y)=ρ(y，x)；
(3)三角不等式，ρ(x，y)≤ρ(x，z)+ρ(z，y)，這裡z也是X中的任意一個元素。
對於R中的任意兩點
定義實函式
，則ρ(x，y)滿足距離的三個條件(1)，(2)，(3)，稱ρ為R上的歐幾里得距離，稱(R，ρ)為n維歐幾里得空間。
定義3設P0∈R是一固定點，δ>0為一實數，則集合{P|ρ(P，P0)<δ)稱為以P0為中心的δ鄰域，記作U(P0，δ)。
P0稱為鄰域的中心，δ稱為鄰域的半徑，某鄰域當不需要指出半徑時，可以簡單地說是P0的某鄰域，記作U(P0)，顯然，在R，R，R中的鄰域U(P0，δ)，就分別是以P0為中心以δ為半徑的開區間、開圓和開球。
容易證明鄰域具有如下基本性質：
(1)對於Q∈U(P)，存在U(Q)
U(P)；
(2)對於P≠Q，存在U(P)和U(Q)，使U(P)∩U(Q)=∅。
定義4設{Pk)是R中一個點列，P0∈R，如果當k→∞時，有ρ(Pk，P0)→0，則稱點列{Pk}收斂於P0，記為
或
。
用鄰域的語言來說，就是：
對P0的任意鄰域U(P0)，存在K∈N，使當k>K時，Pk∈U(P0)．
用“ε一N”語言來說，就是：對任意的ε>0，存在K∈N，使當k>K時，ρ(Pk，P0)<ε．
定義5設A，B是兩個非空點集，A與B的距離定義為
